О теореме Виета
Теорема, выражающая связь между коэффициентами квадратного уравнения и
его корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. Следующим образом: «Если B+D, умноженное на А-А , равно BD, то А равно В и равно D».
Чтобы понять Виета, следует помнить, что А, как и всякая гласная буква , означало у него неизвестное (наше х), гласные же B,D- кэффициенты при неизвестном.
На языке современной алгебры вышеприведенная формулировка Виета означает:
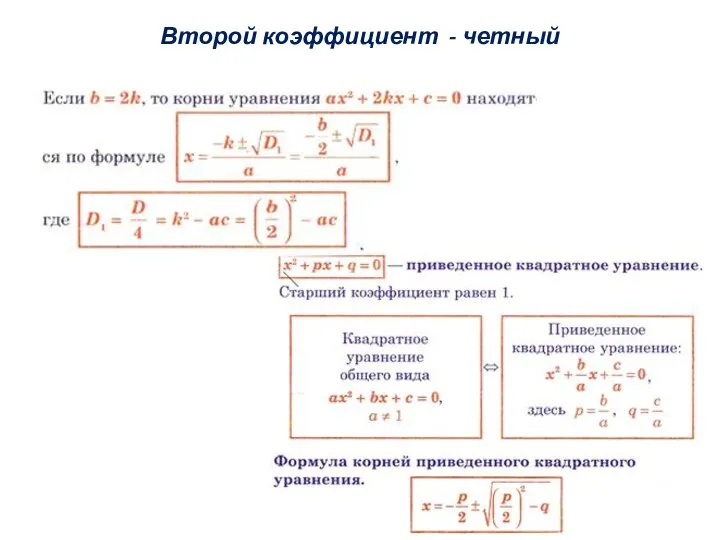
Если приведенное квадратное уравнение x2+px+q=0 имеет действительные корни, то их сумма равна -p, а произведение равно q, то есть
x1 + x2 = -p ,
x1 x2 = q
(сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену).







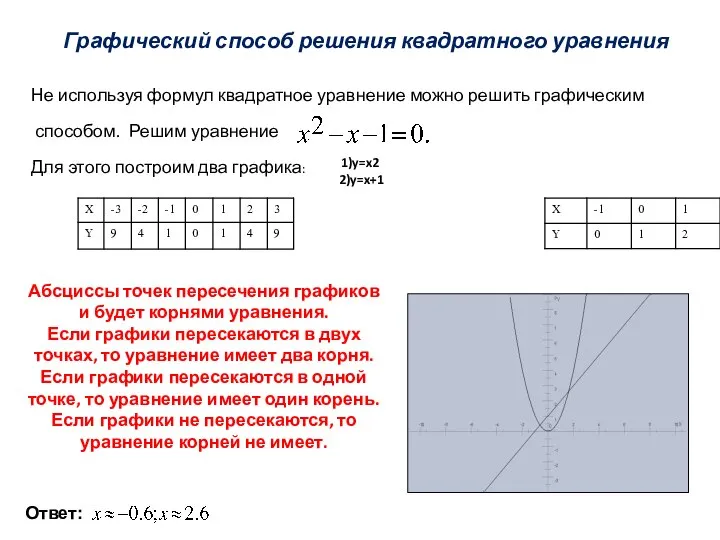

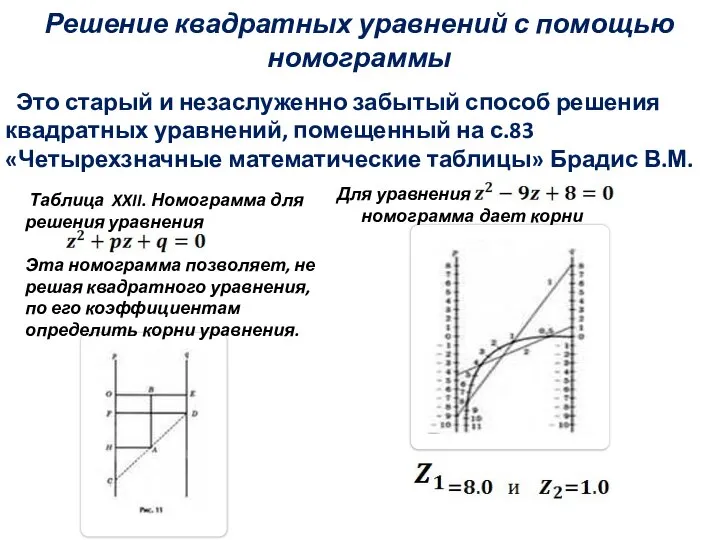
 Геометрическое место точек. Окружность и круг
Геометрическое место точек. Окружность и круг Показательные уравнения
Показательные уравнения Задача Коши для уравнения первого порядка
Задача Коши для уравнения первого порядка Умножение с увлечением
Умножение с увлечением «А в попугаях я всё-таки длиннее» С чего начались измерения… Авторы: Уч-ся 8 класса Камышинский район Волгоградской области МБОУ Воднобуерачная СОШ
«А в попугаях я всё-таки длиннее» С чего начались измерения… Авторы: Уч-ся 8 класса Камышинский район Волгоградской области МБОУ Воднобуерачная СОШ Анализ вариационных рядов. Предмет и задачи математической статистики. (Глава 1.1)
Анализ вариационных рядов. Предмет и задачи математической статистики. (Глава 1.1) Решение уравнений 6 класс
Решение уравнений 6 класс Элементы математической логики
Элементы математической логики Графики. Парабола
Графики. Парабола Координаты середины отрезка.
Координаты середины отрезка.  Логическое следование
Логическое следование Решение задач на совместную работу
Решение задач на совместную работу Прямая и плоскость в прстранстве
Прямая и плоскость в прстранстве Соотношения между сторонами и углами прямоугольного треугольника. Теорема синусов. Теорема косинусов
Соотношения между сторонами и углами прямоугольного треугольника. Теорема синусов. Теорема косинусов Игра-тренажёр «Помоги освободить принцессу». Счёт в пределах 10 +2, -2
Игра-тренажёр «Помоги освободить принцессу». Счёт в пределах 10 +2, -2 Во владениях королевы статистики
Во владениях королевы статистики Число и цифра 4
Число и цифра 4 Численное диференцирование
Численное диференцирование Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Математик – бизнесмен. Математическая игра для 7 классов
Математик – бизнесмен. Математическая игра для 7 классов Задачи на перекраивание фигур
Задачи на перекраивание фигур Абсолютные и относительные величины в статистике
Абсолютные и относительные величины в статистике Презентация на тему Графики тригонометрических функций
Презентация на тему Графики тригонометрических функций  Урок математики. 3 класс Тема урока: Числитель и знаменатель дроби. Запись дробей.
Урок математики. 3 класс Тема урока: Числитель и знаменатель дроби. Запись дробей. Многоугольники, описанные около окружности
Многоугольники, описанные около окружности Призма. Определение призмы
Призма. Определение призмы Перпендикулярность прямой и плоскости Расстояние от точки до плоскости. (2 урок)
Перпендикулярность прямой и плоскости Расстояние от точки до плоскости. (2 урок) Сложение чисел
Сложение чисел