Содержание
- 2. Общий вид СНУ где F – функции нескольких переменных, х – неизвестные n –порядок системы
- 3. Методы решения СНУ: 1. Прямых методов для решения СНУ не существует. 2. Итерационные методы. Методы являются
- 4. Метод Зейделя (метод простых итераций) Ограниченный круг СНУ Исходные данные: Fi(x1, x2,…, xn) Х(0) Е
- 5. Требование Функции Fi(x1, x2,…, xn) должны быть непрерывны в окрестности точки истинного решения Х и точки
- 6. Метод Зейделя на примере СНУ 3-го порядка Из 1-го уравнения выражаем неизвестное х1. Из 2-го уравнения
- 7. Получим новую систему: 2. В правую часть 1-го уравнения подставляем начальные приближения неизвестных х2(0) и х3(0).
- 8. 5. Далее рассчитывается разность между значениями начальных приближений и уточненными значениями неизвестных. Если то считается, что
- 9. ЗАМЕЧАНИЕ Метод Зейделя применим, если неизвестные из соответствующих уравнений можно выразить в явном виде. Метод Зейделя
- 10. Примеры:
- 11. Метод Ньютона для решения СНУ Основа: разложение функций в ряд Тейлора относительно значений начальных приближений неизвестных.
- 12. Для реализации метода Ньютона необходимо задать следующие данные: 1. Выражения для функций F1, F2 ,…, Fn
- 13. Требование Функции Fi(x1, x2,…, xn) должны быть непрерывны и дифференцируемы в окрестности точки истинного решения Х
- 14. Метод Ньютона на примере СНУ 3-го порядка Задано: x10, x20 и x30. Истинное решение системы: x1,
- 15. F1, F2 и F3 разлагаются в ряд Тейлора. Члены, содержащие производные старше первого порядка отбрасываются. Преобразуем
- 16. Получим систему линейных алгебраических уравнений: Неизвестные - Δx1, Δx2 и Δx3, Вектор-столбец свободных членов – F1,
- 17. СЛАУ решается любым известным методом (метод Гаусса, метод Крамера), получаем значения неизвестных Δx1, Δx2 и Δx3
- 18. Если полученные значения Δx1 и Δx2 и Δx3 по модулю оказались менее заданной точности Е, то
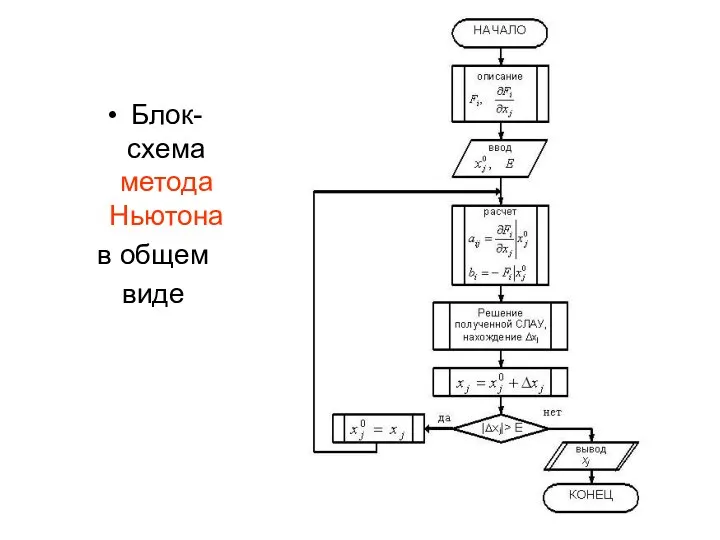
- 19. Блок-схема метода Ньютона в общем виде
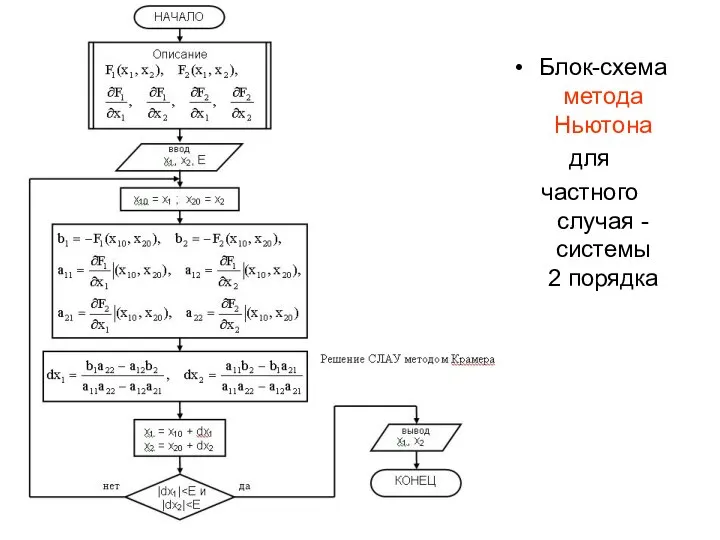
- 20. Блок-схема метода Ньютона для частного случая - системы 2 порядка
- 22. Скачать презентацию

















 Сложение и вычитание смешанных дробей
Сложение и вычитание смешанных дробей Решение текстовых задач
Решение текстовых задач Число «Пи» вокруг нас. МОУ СОШ №7 Г. Тверь
Число «Пи» вокруг нас. МОУ СОШ №7 Г. Тверь График квадратичной функции
График квадратичной функции Геометрический смысл производной
Геометрический смысл производной Сложение натуральных чисел. 5 класс
Сложение натуральных чисел. 5 класс Натуральные числа. Смешанные числа
Натуральные числа. Смешанные числа Математика и биология
Математика и биология Сумма углов треугольника
Сумма углов треугольника Перпендикуляр и наклонная
Перпендикуляр и наклонная Алиасинг эффект. АЦП σ-δ. Интегратор
Алиасинг эффект. АЦП σ-δ. Интегратор Решение задач по теме «Подобные слагаемые»
Решение задач по теме «Подобные слагаемые» Равномерное прямолинейное движение. Тест №1
Равномерное прямолинейное движение. Тест №1 Урок геометрии в 9 классе Пирамида
Урок геометрии в 9 классе Пирамида «Экскурсия по летнему саду».
«Экскурсия по летнему саду». Скажи мне – и я забуду, покажи мне – и я запомню, дай сделать – и я пойму. Конфуций.
Скажи мне – и я забуду, покажи мне – и я запомню, дай сделать – и я пойму. Конфуций. Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Длина окружности. Площадь круга
Длина окружности. Площадь круга Действия с десятичными дробями
Действия с десятичными дробями Моделирование зависимостей между величинами
Моделирование зависимостей между величинами Математика. Повторение. 1 класс
Математика. Повторение. 1 класс Extracurricular study in mathematics, 7th grade
Extracurricular study in mathematics, 7th grade Применение производной для исследования функций на монотонность и экстремумы
Применение производной для исследования функций на монотонность и экстремумы ТЕМА: «Деление многозначного числа на однозначное»
ТЕМА: «Деление многозначного числа на однозначное» Введение декартовых координат в пространстве. Расстояние между точками. Координаты середины отрезка
Введение декартовых координат в пространстве. Расстояние между точками. Координаты середины отрезка Решение заданий ГИА. Модуль Геометрия
Решение заданий ГИА. Модуль Геометрия Какое число пропущено? Тест по математике в 5 классе по теме: «Нумерация в пределах 1000»
Какое число пропущено? Тест по математике в 5 классе по теме: «Нумерация в пределах 1000» Графики тригонометрических функций
Графики тригонометрических функций