Содержание
- 2. ФУНКЦИЯ МНОГИХ ПЕРЕМЕННЫХ Случаи функций двух переменных z = f(x, y) и трех переменных (например, распределение
- 10. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 12. ЧАСТНЫЕ ПРОИЗВОДНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 13. ЧАСТНЫЕ ПРОИЗВОДНЫЕ Для наглядности, здесь и далее все определения и утверждения будем формулировать для функции 2-х
- 14. ОПРЕДЕЛЕНИЕ. Предел при Δx → 0 отношения (если он существует и конечен) называется частной производной функции
- 15. Замечания. 1) Обозначения и надо понимать как целые символы, а не как частное двух величин. Отдельно
- 16. Соответствие и является функцией, определенной на D1(D2)⊆ D(f). Ее называют частной производной функции z = f(x,y)
- 18. Фактически, – это обыкновенная производная функции z = f(x,y), рассматриваемой как функция одной переменной x (соответственно
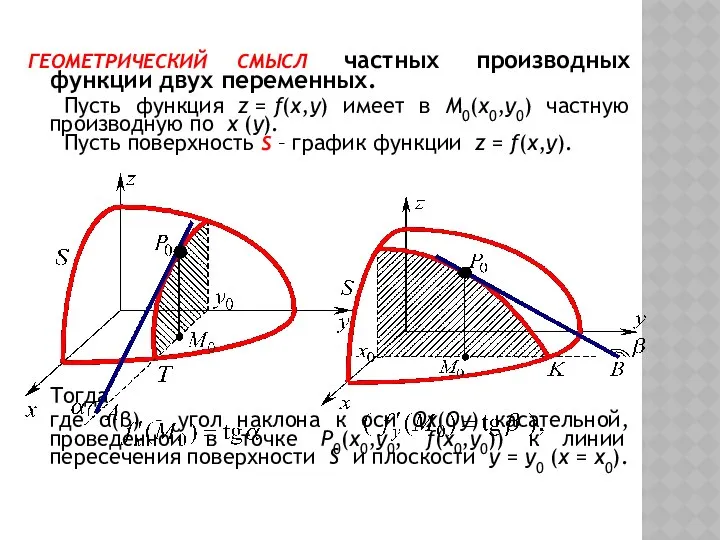
- 24. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ частных производных функции двух переменных. Пусть функция z = f(x,y) имеет в M0(x0,y0) частную
- 25. ГРАДИЕНТ
- 26. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 2-ГО ПОРЯДКА
- 27. ДИФФЕРЕНЦИАЛ 2-ГО ПОРЯДКА
- 29. Скачать презентацию




















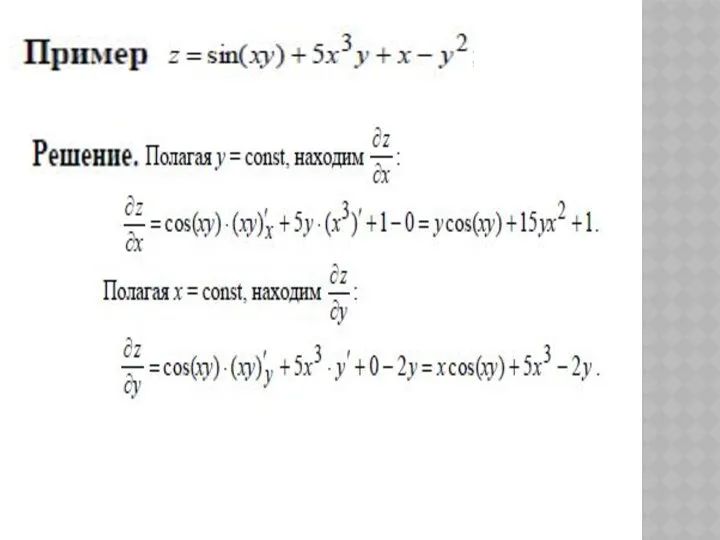




 Формулы для координат точки. Площадь треугольника. Г. Екаиеринбург МОУ-гимназия №13 Анкина Т.С.
Формулы для координат точки. Площадь треугольника. Г. Екаиеринбург МОУ-гимназия №13 Анкина Т.С.  Десятичная запись дробных чисел
Десятичная запись дробных чисел Сравните величины: 4 мин 3 с и 213 с
Сравните величины: 4 мин 3 с и 213 с Логика. Логические задачи (составление таблиц)
Логика. Логические задачи (составление таблиц) Иррациональные числа. История открытия
Иррациональные числа. История открытия Квадратный корень. История математических обозначений
Квадратный корень. История математических обозначений Аттестационная работа. Решение задач на комбинации многогранников и тел вращения
Аттестационная работа. Решение задач на комбинации многогранников и тел вращения МАТЕМАТИКА 3 класс ГБОУ гимназия 1506 учитель начальных классов Моргачёва Елена Владимировна
МАТЕМАТИКА 3 класс ГБОУ гимназия 1506 учитель начальных классов Моргачёва Елена Владимировна  Обыкновенные дроби
Обыкновенные дроби Квадратичная функция и ее свойства
Квадратичная функция и ее свойства Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Стереометрия аксиомалары
Стереометрия аксиомалары Тренировочный вариант №98
Тренировочный вариант №98 Презентация по математике "Веселый поезд" - скачать
Презентация по математике "Веселый поезд" - скачать  Физическое и математическое моделирование
Физическое и математическое моделирование Векторы. Геометрия (9 класс)
Векторы. Геометрия (9 класс) Презентация по математике "Понятие окружности" - скачать бесплатно
Презентация по математике "Понятие окружности" - скачать бесплатно ВПМ. Математичне програмування та дослідження операцій. Задачі з умовами невизначеності та конфлікту. (Лекція 4)
ВПМ. Математичне програмування та дослідження операцій. Задачі з умовами невизначеності та конфлікту. (Лекція 4) Презентация по математике "Закрепление смысла нового арифметического действия умножения" - скачать
Презентация по математике "Закрепление смысла нового арифметического действия умножения" - скачать  Параллельность прямых и плоскостей в пространстве
Параллельность прямых и плоскостей в пространстве Подготовка к ЕГЭ
Подготовка к ЕГЭ Сложение и вычитание целых чисел с разными знаками
Сложение и вычитание целых чисел с разными знаками Тела вращения. Сечения. Комбинации
Тела вращения. Сечения. Комбинации Теорема об отрезках пересекающихся хорд. Центральные и вписанные углы
Теорема об отрезках пересекающихся хорд. Центральные и вписанные углы Параллельность плоскостей
Параллельность плоскостей Признак перпендикулярности прямой и плоскости. (10 класс)
Признак перпендикулярности прямой и плоскости. (10 класс) Индивидуальный проект на тему "Золотое сечение в природе"
Индивидуальный проект на тему "Золотое сечение в природе" Презентация по математике "Геометрический смысл производной" - скачать
Презентация по математике "Геометрический смысл производной" - скачать