Элементы математической логики

Высказывания

Предложение, о котором имеет смысл говорить, что оно является истинным или

Значение истинности высказывания

Элементарные и сложные высказывания

Если никакая часть высказывания сама по себе не

Операции над высказываниями

1. Инверсия ( логическое отрицание)
2. Дизъюнкция (логическое сложение)
3.

Обозначения и значение

Основные законы логики

1. Закон тождества
2. Закон непротиворечия
3. Закон исключения третьего
4. Закон

Закон тождества

Всякое высказывание тождественно са­мому себе:
А = А

Закон непротиворечия

Закон исключения третьего

Закон отрицания отрицания

Пример задачи

Трое подозреваемых в преступлении Иванов, Петров и Сидоров дали следующие

Построить таблицу истинности каждого высказывания и по ней определить:
а) Кто

Введем простые высказывания: А={виновен Иванов};
В={виновен Петров};
С={виновен Сидоров}.

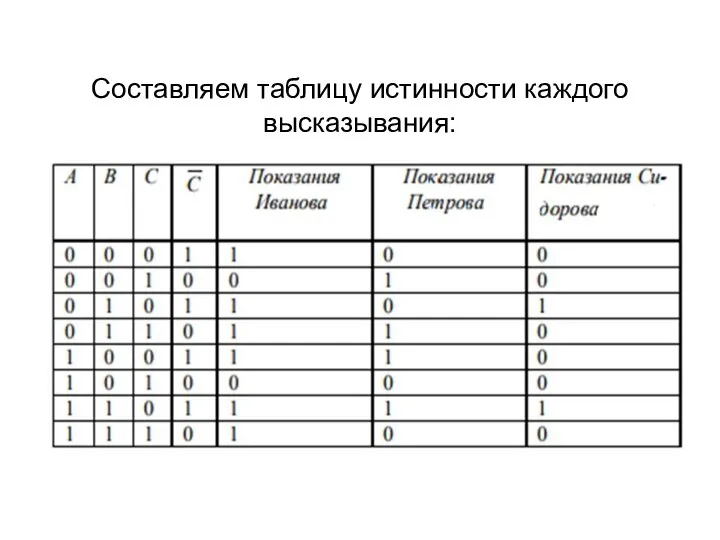
Составляем таблицу истинности каждого высказывания:

а) Если все говорят правду, то в показаниях (последние три столбца)

б) Если все лгут, то в показаниях должны быть три нуля.

в) Условию того, что все виновны, соответствует последняя строка, у которой

г) Условию того, что все невиновны, соответствует первая строка, у которой