Содержание
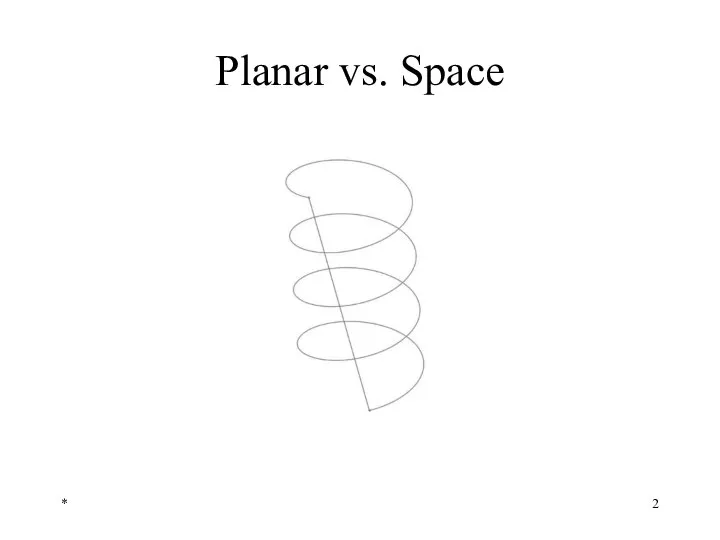
- 2. * Planar vs. Space
- 3. * Analytic (known form) vs. Synthetic (free form) Creating these curves by using known analytic curve
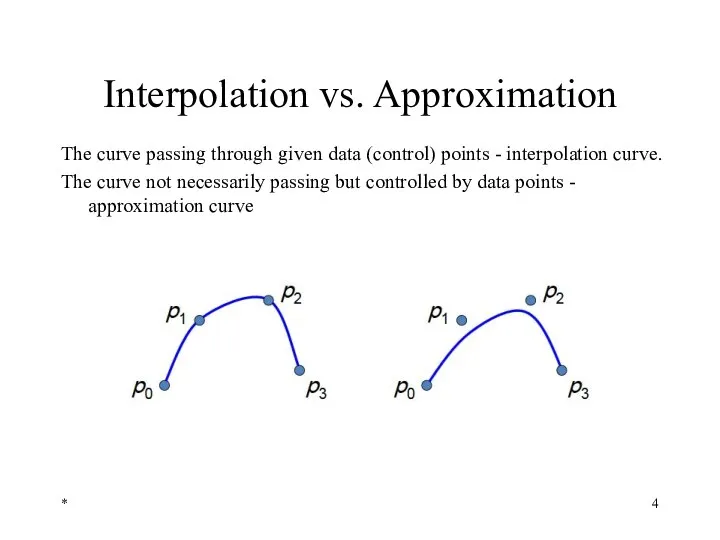
- 4. * Interpolation vs. Approximation The curve passing through given data (control) points - interpolation curve. The
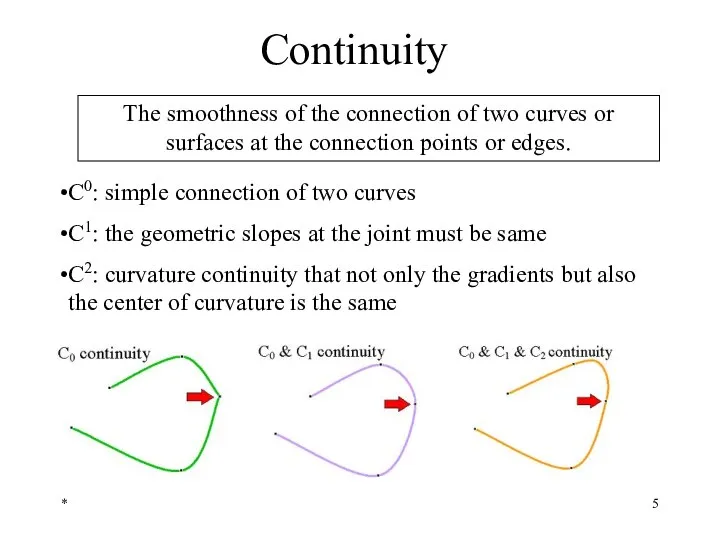
- 5. * Continuity The smoothness of the connection of two curves or surfaces at the connection points
- 6. * Cubic Curves In an expanded vector form: Parametric equation of a cubic spline segment: where
- 7. * Hermite Cubic Splines Hermite form of a general cubic spline is defined by positions and
- 8. * Hermite Cubic Splines
- 9. * Hermite Cubic Spline – Tangent Vector
- 10. * X Hermite Cubic Splines - example The Hermite curve fits the points: P0 = [1,1]T,
- 11. * Bezier Curves - sl. 1 Parametric equation of Bezier curve where P(u) is the position
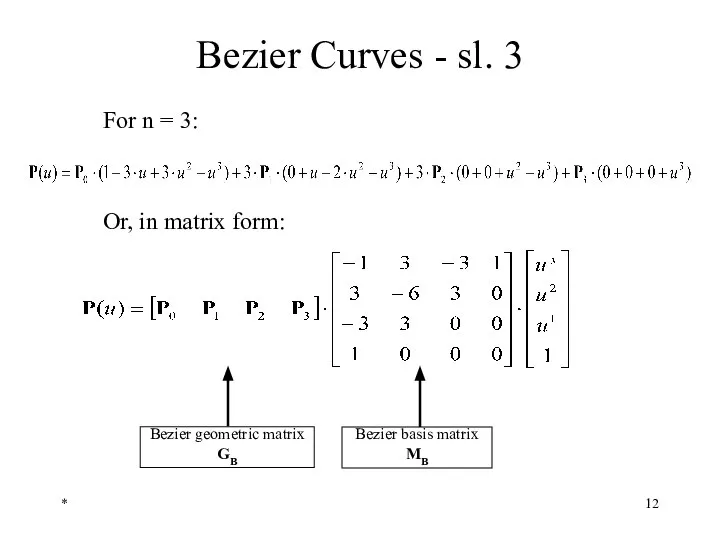
- 12. * Bezier Curves - sl. 3 For n = 3: Bezier basis matrix MB Or, in
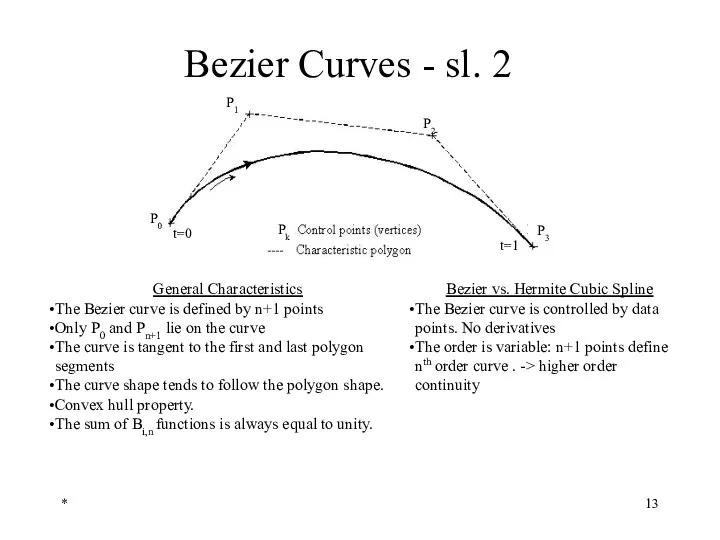
- 13. * Bezier Curves - sl. 2 General Characteristics The Bezier curve is defined by n+1 points
- 14. * Bezier Curves - sl. 5 Practice The coordinates of 4 control points are given: P0
- 15. * Bezier Curves - sl. 4
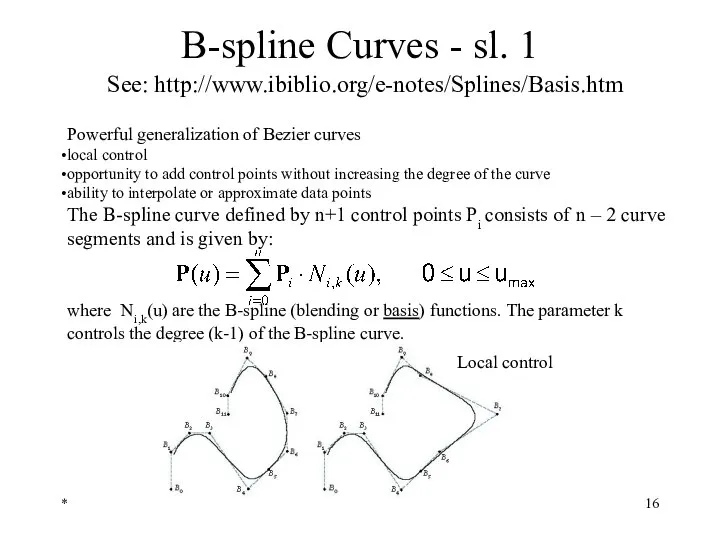
- 16. * B-spline Curves - sl. 1 See: http://www.ibiblio.org/e-notes/Splines/Basis.htm Powerful generalization of Bezier curves local control opportunity
- 17. * B-spline Curves - sl. 2 See: http://www.ibiblio.org/e-notes/Splines/Basis.htm The B-spline curve defined by n+1 control points
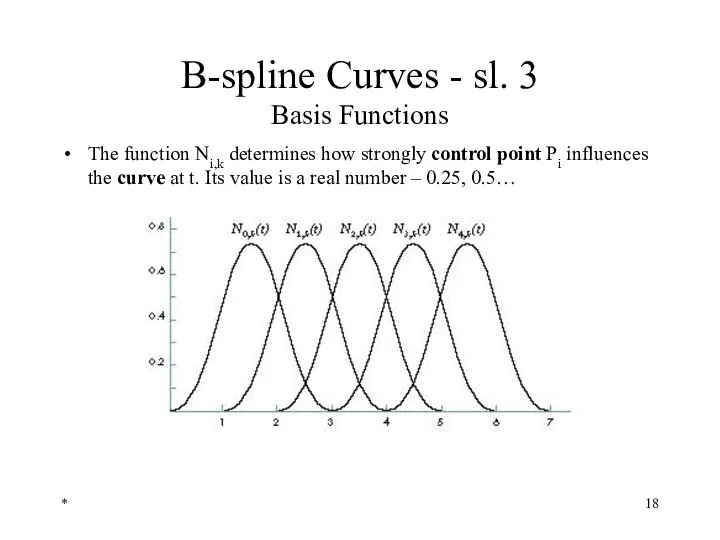
- 18. * B-spline Curves - sl. 3 Basis Functions The function Ni,k determines how strongly control point
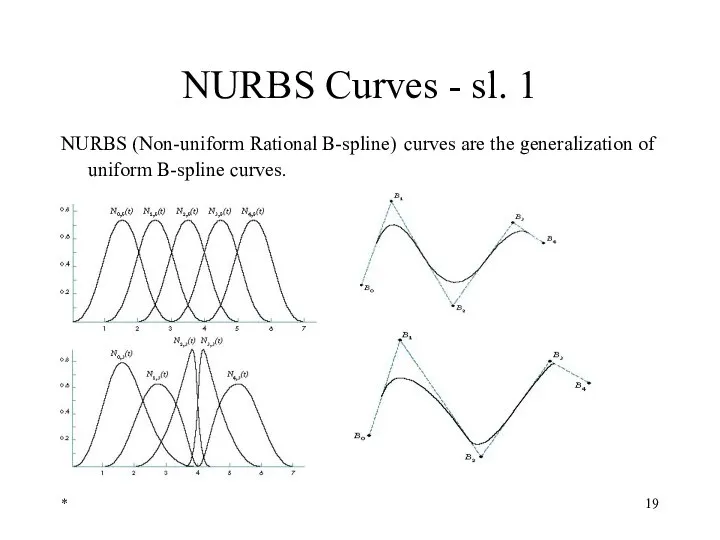
- 19. * NURBS Curves - sl. 1 NURBS (Non-uniform Rational B-spline) curves are the generalization of uniform
- 21. Скачать презентацию










 Логика и алгебра высказываний
Логика и алгебра высказываний Устный счет
Устный счет  Деление натуральных чисел
Деление натуральных чисел Магия чисел. Нумерология
Магия чисел. Нумерология Готовимся к ЕГЭ. Задание 23-24
Готовимся к ЕГЭ. Задание 23-24 Степень с рациональным и действительным показателем
Степень с рациональным и действительным показателем Перпендикуляр и наклонная к прямой
Перпендикуляр и наклонная к прямой Обыкновенные дроби и их применение
Обыкновенные дроби и их применение Методи вирішення нелінійних рівнянь. (Лекція 3)
Методи вирішення нелінійних рівнянь. (Лекція 3) Мы - строители. Обучающая игра-тренажёр. Часть 1
Мы - строители. Обучающая игра-тренажёр. Часть 1 Вклад мусульманских ученых в развитие геометрии и тригонометрии
Вклад мусульманских ученых в развитие геометрии и тригонометрии Признаки делимости на 2, 5, 10, 4 и 25. Урок 106
Признаки делимости на 2, 5, 10, 4 и 25. Урок 106 Применение свойств арифметического квадратного корня
Применение свойств арифметического квадратного корня Справочник по планиметрии. (7-9 класс)
Справочник по планиметрии. (7-9 класс) Сочетательное свойство умножения и сложения
Сочетательное свойство умножения и сложения Решение неравенств ГБОУ СОШ №1084 Учитель математики Смирнова Н.В.
Решение неравенств ГБОУ СОШ №1084 Учитель математики Смирнова Н.В. Состав числа 12
Состав числа 12 Определение синуса, косинуса и тангенса угла
Определение синуса, косинуса и тангенса угла Алгебраические выражения
Алгебраические выражения Дроби и проценты 6 класс Мовсесова Л.В.
Дроби и проценты 6 класс Мовсесова Л.В. Нумерология
Нумерология Построение графиков функций, содержащих модуль 8 класс Учитель математики МБОУ СОШ № 117 Щербина Антонина Николаевна
Построение графиков функций, содержащих модуль 8 класс Учитель математики МБОУ СОШ № 117 Щербина Антонина Николаевна  Нахождение дроби от числа
Нахождение дроби от числа Презентация по математике "Цель урока – спасти книги" - скачать бесплатно
Презентация по математике "Цель урока – спасти книги" - скачать бесплатно Рюкзак. Восстановление ответа
Рюкзак. Восстановление ответа Проверка статистических гипотез
Проверка статистических гипотез Графы и деревья. Кроссворд
Графы и деревья. Кроссворд Множественные связи. Порядковые и категоризованные переменные
Множественные связи. Порядковые и категоризованные переменные