- Главная
- Математика
- Геометрические преобразования

Содержание
- 2. Геометрические преобразования − взаимно однозначные отображения прямой, плоскости или пространства на себя. Обычно рассматривают такие совокупности
- 3. Пропедевтика изучения темы: знакомство с симметрией в курсе математики 1-6 классов. Симметрия в искусстве. Понятие движения.
- 4. С реальными преобразованиями предметов мы имеем дело постоянно: изображая пространственные фигуры, мы преобразуем эти фигуры в
- 5. Сравнив эти два определения, видим их полную аналогию. Но в определении функции речь идет о сопоставлении
- 6. Точка Х называется неподвижной точкой преобразования f, если f(X)=X. Например, при проектировании фигуры М на прямую
- 7. Пусть Φ1 =f(Φ) и Φ2 = g(Φ1) . В итоге фигура Φ переводится в фигуру Φ2
- 8. Преобразования могут быть очень разнообразны: есть преобразования, которые изменяют форму фигуры. Есть преобразования, которые, хоть и
- 9. Движение в геометрии − преобразования пространства, сохраняющие свойства фигур (размеры, форму и др. ). Понятие движения
- 10. Движение называют собственным или несобственным в зависимости от того, сохраняет ли оно или меняет ориентацию, Всякое
- 11. Поворот плоскости вокруг центра O на угол α. Обозначение: или Свойство поворотов: (n - целое). Композиция
- 12. Центральная симметрия (относительно точки O) на плоскости. Определение и обозначение: Композиция центральных симметрий: (1) с общим
- 13. Осевая симметрия (симметрия относительно прямой l) на плоскости. Обозначение: Sl , l − ось симметрии Композиция
- 14. Параллельный перенос на вектор . Обозначение: Координатные формулы параллельного переноса на вектор , если А(0,0), В(а,
- 15. Выясним более подробно связь того движения, которое определяется в геометрии, с реальным движением тел. Представим себе
- 16. В геометрическом понятии движения удерживают только сопоставление одного положения тела с другим, вовсе отвлекаясь от процесса
- 17. Симметрия (от греческого -συμμετρία- означает соразмерность) - это пропорциональность или гармония в расположении одинаковых предметов какой-либо
- 18. Симметрия очень широко распространена в природе и в творениях человека. В творениях человека симметрия больше всего
- 19. Подобие с коэффициентом k. Обозначение: Определение: если k>0 и Х1 = F k(X) и Y1 =
- 20. Подобные фигуры Обозначение: (фигура Φ1 подобна фигуре Φ2 с коэффициентом k). Свойства подобных фигур: 1) рефлексивность:
- 21. Зеркальная симметрия. Зафиксируем некоторую плоскость α. Симметрией относительно плоскости α называется преобразование фигуры, которое каждой ее
- 22. Параллельное проектирование. Рассмотрим в пространстве некоторую прямую р, пересекающую плоскость α. Через каждую точку Х пространства
- 24. Скачать презентацию
Геометрические преобразования − взаимно однозначные отображения прямой, плоскости или пространства
Геометрические преобразования − взаимно однозначные отображения прямой, плоскости или пространства
Примерами геометрических преобразований, образующих группу преобразований, могут служить движения плоскости (или пространства), аффинные преобразования, проективные преобразования.
В современных школьных программах понятию геометрического преобразования отводится достаточно скромное место: рассматриваются движения плоскости/пространства и преобразования подобия − в курсе геометрии, а также некоторые случаи аффинных преобразований графиков функций − в курсе алгебры.
Школьникам дают понятия таких преобразований как поворот, параллельный перенос, симметрия, иногда инверсия, и показывают, что эти преобразования могут быть полезны при решении определенных задач.
РОЛЬ И МЕСТО ТЕМЫ «ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ» В ШКМ
Пропедевтика изучения темы: знакомство с симметрией в курсе математики 1-6
Пропедевтика изучения темы: знакомство с симметрией в курсе математики 1-6
Понятие движения. Основные виды движений. Равенство фигур.
Понятие подобия как преобразования плоскости. Гомотетия. Подобные фигуры.
Понятие геометрического преобразования. Геометрические преобразования пространства (движение и подобие в пространстве).
Параллельное проектирование
Фигуры вращения (конус, цилиндр, шар)
Применение теории геометрических преобразований к решению геометрических задач. Симметрия плоских фигур..
ОСНОВНЫЕ НАПРАВЛЕНИЯ ИЗУЧЕНИЯ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ
С реальными преобразованиями предметов мы имеем дело постоянно: изображая пространственные
С реальными преобразованиями предметов мы имеем дело постоянно: изображая пространственные
Понятие геометрического преобразования очень похоже на понятие числовой функции. Напомним известное из курса алгебры определение функции:
Если каждому числу x из некоторого множества чисел M поставлено в соответствие определенное число, обозначаемое f(x), то говорят, что на множестве M задана функция f.
А теперь сформулируем определение преобразования фигуры.
Если каждой точке X некоторой фигуры Φ поставлена в соответствие
определенная точка, обозначаемая f(X), то говорят, что задано
преобразование f множества Φ.
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
В ШКМ
Сравнив эти два определения, видим их полную аналогию. Но в
Сравнив эти два определения, видим их полную аналогию. Но в
Можно даже сказать, что преобразование фигуры - это задание на ней функции, аргументами и значениями которой являются точки. С другой стороны, задав функцию f(x) на некотором числовом множестве, например, на отрезке [a,b], мы можем также считать, что задали преобразование отрезка [a,b]. В этом случае график функции f(x) помогает нам определить положение образа любой точки этого отрезка.
Примером преобразования фигуры является проектирование ее на прямую или на плоскость. Вспомните, что проектирование фигуры Φ на прямую (на плоскость) состоит в том, что каждой точке Х фигуры Φ сопоставляется ее проекция Х1 на эту прямую (на эту плоскость).
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
В ШКМ
Точка Х называется неподвижной точкой преобразования f, если f(X)=X. Например,
Точка Х называется неподвижной точкой преобразования f, если f(X)=X. Например,
То преобразование фигуры, все точки которого неподвижны, называется тождественным преобразованием фигуры. Тождественное преобразование мы обозначаем буквой Е. Мы увидим, что и такие простые преобразования необходимы в теории преобразований.
Образом фигуры Φ при преобразовании f называется фигура (ее обозначают f(Φ)) , состоящая из образов всех точек X фигуры Φ. Например, образ наклонной АС к прямой а при проектировании отрезка АС на а − это его проекция АВ на прямую а. А образом прямой р, перпендикулярной плоскости α, при проектировании на α является точка О, в которой пересекаются р и α
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
В ШКМ
Пусть Φ1 =f(Φ) и Φ2 = g(Φ1) . В итоге
Пусть Φ1 =f(Φ) и Φ2 = g(Φ1) . В итоге
С композицией преобразований школьники встречались в курсе алгебры, когда рассматривали, например, такие функции:
Некоторым композициям преобразований дают специальные названия.
Например, композицию осевой симметрии и параллельного переноса на вектор, параллельный оси симметрии, называют скользящей осевой симметрией .
Композицию зеркальной симметрии и параллельного переноса на вектор, параллельный плоскости симметрии, называют скользящей зеркальной симметрией .
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
В ШКМ
Преобразования могут быть очень разнообразны: есть преобразования, которые изменяют форму
Преобразования могут быть очень разнообразны: есть преобразования, которые изменяют форму
Знакомство с двумя важнейшими классами геометрических преобразований начинают с класса тех преобразований, которые сохраняют все свойства фигур. Следует обратить внимание учащихся на то, что любое геометрическое свойство можно выразить через расстояния между точками, через длины соединяющих эти точки отрезков. И геометрические величины выражаются через расстояния. Например, мы умеем находить углы и площадь треугольника, зная длины его сторон. Следовательно, мы знаем, как найти площадь и углы любого многоугольника, если известны все расстояния между его вершинами. Точно так же, зная все расстояния между вершинами многогранника, можно найти площадь его поверхности и его объем. Поэтому те преобразования, которые сохраняют расстояния, сохраняют и все другие свойства геометрических фигур. Такие преобразования называют движениями.
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
В ШКМ
Движение в геометрии − преобразования пространства, сохраняющие свойства фигур (размеры,
Движение в геометрии − преобразования пространства, сохраняющие свойства фигур (размеры,
Понятие движения сформировалось путем абстракции реальных перемещении твердых тел.
Движение евклидова пространства − геометрическое преобразование пространства, сохраняющее расстояния между точками (образом треугольника при движении является равный ему треугольник). Движение есть ортогональное преобразование.
Важную роль понятие движение играет в римановых пространствах теории относительности (сильная асимметрия гравитационных полей накладывает ограничения на движения твёрдых тел в таких пространствах).
Движение может быть принято в качестве основного понятия при аксиоматическом построении геометрии. В этом случае вместо аксиом равенства вводятся аксиомы движения. Равенство отрезков, углов и др. фигур определяется через понятие движения (фигуры называются равными, если одна переходит в другую при помощи некоторого движения).
Совокупность движений образует группу.
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ: ДВИЖЕНИЕ
Движение называют собственным или несобственным в зависимости от того, сохраняет
Движение называют собственным или несобственным в зависимости от того, сохраняет
Всякое собственное движение может быть представлено либо как параллельный перенос, либо как вращение вокруг некоторой точки. Собственное движение в пространстве есть или вращение вокруг оси, или параллельный перенос, или же может быть представлено в виде винтового движения (вращения вокруг оси и параллельного переноса в направлении этой оси).
Любое несобственное движение представимо в виде композиции параллельного переноса вдоль некоторого направления и симметрии относительно прямой, имеющей то же самое направление. Несобственное движение в пространстве есть либо симметрия относительно плоскости, либо может быть представлено в виде произведения симметрии относительно плоскости на вращение вокруг оси, перпендикулярной этой плоскости, либо в виде произведения симметрии относительно плоскости на перенос в направлении вектора, параллельного этой плоскости.
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ: ДВИЖЕНИЕ
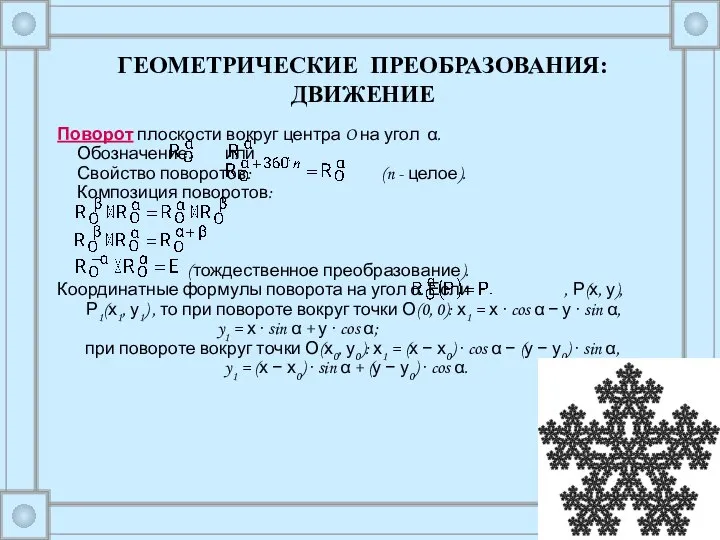
Поворот плоскости вокруг центра O на угол α.
Обозначение:
Поворот плоскости вокруг центра O на угол α.
Обозначение:
Свойство поворотов: (n - целое).
Композиция поворотов:
(тождественное преобразование).
Координатные формулы поворота на угол α. Если , Р(х, у), Р1(х1, у1) , то при повороте вокруг точки О(0, 0): х1 = х ∙ cos α − у ∙ sin α,
y1 = х ∙ sin α + у ∙ cos α;
при повороте вокруг точки О(х0, у0): х1 = (х − х0) ∙ cos α − (у − у0) ∙ sin α,
y1 = (х − х0) ∙ sin α + (у − у0) ∙ cos α.
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ: ДВИЖЕНИЕ
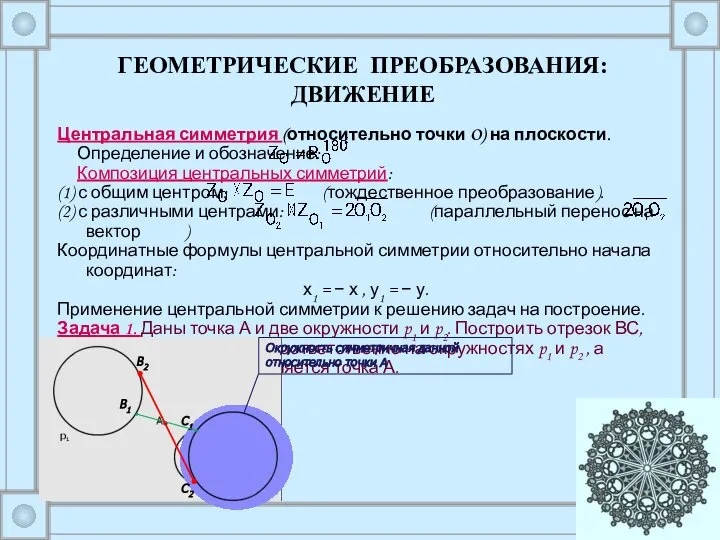
Центральная симметрия (относительно точки O) на плоскости.
Определение и
Центральная симметрия (относительно точки O) на плоскости.
Определение и
Композиция центральных симметрий:
(1) с общим центром: (тождественное преобразование).
(2) с различными центрами: (параллельный перенос на вектор )
Координатные формулы центральной симметрии относительно начала координат:
х1 = − х , у1 = − у.
Применение центральной симметрии к решению задач на построение.
Задача 1. Даны точка А и две окружности p1 и p2. Построить отрезок ВС, концы которого лежат соответственно на окружностях p1 и p2 , а серединой которого является точка А.
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ: ДВИЖЕНИЕ
С1
С2
В1
В2
Окружность симметричная данной относительно точки А
Осевая симметрия (симметрия относительно прямой l) на плоскости.
Обозначение:
Осевая симметрия (симметрия относительно прямой l) на плоскости.
Обозначение:
Композиция осевых симметрий:
(1) если l1 ⊥ l2 и O = l1 ∩l2, то (центральная симметрия).
(2) если l1 || l2 , то (параллельный перенос)
Координатные формулы осевой симметрии
относительно оси ОУ: х1 = − х , у1 = у,
относительно оси ОХ: х1 = х , у1 = − у,
относительно прямой х = у: х1 = у , у1 = х.
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ: ДВИЖЕНИЕ
Параллельный перенос на вектор .
Обозначение:
Координатные формулы параллельного переноса
Параллельный перенос на вектор .
Обозначение:
Координатные формулы параллельного переноса
х1 = х + а , у1 = у + b.
Преобразование, обратное к параллельному переносу на вектор есть параллельный перенос на вектор .
Свойство:
(1) коммутативность:
Множество всех параллельных переносов является группой.
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ: ДВИЖЕНИЕ
Выясним более подробно связь того движения, которое определяется в геометрии,
Выясним более подробно связь того движения, которое определяется в геометрии,
Представим себе какое-нибудь реальное тело в некотором определенном положении. Каждая его частица занимает определенное положение – находится в определенной точке Х пространства. Допустим, предмет изменил свое положение. Это значит, каждая его частица заняла некоторое новое (или, в частности, старое) положение. Данная частица, бывшая в точке Х, заняла положение в точке пространства X1; тем самым движение предмета устанавливает соответствие между точками пространства: точка X1 соответствует точке Х. (Можно сказать еще так: «месту Х, где находилась частица, соответствует место X1, где она теперь находится»).
В механике тело называется твердым или даже абсолютно твердым, если оно не допускает никаких деформаций, так что расстояния между его частицами неизменны. Поэтому, если при движении такого тела две его частицы Х и Y перешли в точки X1 и Y1, то расстояния сохраняются: ХУ= X1 У1 , т.е. происходит движение,
как мы его определили геометрически.
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ: ДВИЖЕНИЕ МЕХАНИЧЕСКОЕ И ГЕОМЕТРИЧЕСКОЕ
В геометрическом понятии движения удерживают только сопоставление одного положения тела
В геометрическом понятии движения удерживают только сопоставление одного положения тела
Любое движение в геометрии представляет собой либо отвлеченный образ реального движения твердого тела, когда учитывается только то, из каких точек пространства в какие точки переходят частицы тела (т.е. учитывается только соответствие одних точек другим), либо сочетание (композицию) этого отвлеченного образа реального движения с зеркальной симметрией.
Только что сказанное о движениях принадлежит не самой геометрии, а ее связи с физикой. Можно сказать, что геометрия здесь выступает как первая глава механики, трактующая механическое движение. Без движения геометрия не могла бы существовать. В самом деле, уже сравнение отрезков и измерение длин основано на движении предметов, когда один прикладывается к другому.
И должно быть понятно, почему Ньютон в предисловии к своему
великому труду «Математические начала натуральной философии»
писал, что геометрия основывается на механике.
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ: ДВИЖЕНИЕ МЕХАНИЧЕСКОЕ И ГЕОМЕТРИЧЕСКОЕ
Симметрия (от греческого -συμμετρία- означает соразмерность) - это пропорциональность или
Симметрия (от греческого -συμμετρία- означает соразмерность) - это пропорциональность или
Отдельные предметы или части симметричного предмета являются как бы отражениями или изображениями друг друга в этих зеркальных плоскостях, называются плоскостями симметрии. Простейшим случаем симметрии является такое расположение частей целого, при котором целое делится на две.
Если группа или предмет состоит лишь из совместимых частей, то в них можно провести так называемые оси симметрии и совместить равные части, повернув их вокруг этих осей. Кроме зеркальных плоскостей и осей симметрии есть еще зеркальная точка, или центр симметрии. В нем делятся пополам все прямые, соединяющие попарно одинаковые точки предметов группы или частей одного предмета. Зеркальная плоскость, ось симметрии и центр симметрии называют элементами симметрии и могут быть сведены к зеркальным плоскостям и их сочетаниям.
Какое-либо нарушение симметрии или её отсутствие вообще называется асимметрией.
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ: СИММЕТРИЯ
Симметрия очень широко распространена в природе и в творениях человека.
Симметрия очень широко распространена в природе и в творениях человека.
В растительном мире также очень распространена симметрия и обнаруживается в расположении органов цветка, частей его листа и даже ветвей. В животном мире симметрия наблюдается не так строго, но также очень распространена. С наружной симметрией стоит в согласии и внутреннее строение животных, растений и кристаллов.
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ: СИММЕТРИЯ В ПРИРОДЕ И В ТВОРЕНИЯХ ЧЕЛОВЕКА
Подобие с коэффициентом k.
Обозначение:
Определение: если k>0
Подобие с коэффициентом k.
Обозначение:
Определение: если k>0
Композиция преобразования подобия:
Гомотетия. Гомотетией с центром O и ненулевым коэффициентом k называется такое преобразование фигуры, которое каждой ее точке X сопоставляет такую точку X1, что выполняется равенство : .
Подобное преобразование фигуры Φ1 в фигуру Φ2 с коэффициентом k можно представить как композицию гомотетии с коэффициентом k и движения.
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ: ПОДОБИЕ
Подобные фигуры
Обозначение: (фигура Φ1 подобна фигуре Φ2 с
Подобные фигуры
Обозначение: (фигура Φ1 подобна фигуре Φ2 с
Свойства подобных фигур:
1) рефлексивность:
2) симметричность:
3) отношение площадей подобных фигур:
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ: ПОДОБНЫЕ ФИГУРЫ
Зеркальная симметрия. Зафиксируем некоторую плоскость α.
Симметрией относительно плоскости α
Зеркальная симметрия. Зафиксируем некоторую плоскость α.
Симметрией относительно плоскости α
ИЗУЧЕНИИ
ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ
В СТАРШЕЙ ШКОЛЕ
Параллельное проектирование. Рассмотрим в пространстве некоторую прямую р, пересекающую плоскость
Параллельное проектирование. Рассмотрим в пространстве некоторую прямую р, пересекающую плоскость
Параллельную проекцию реальной фигуры представляет собой, например, её тень, падающая на плоскую поверхность при солнечном
освещении, поскольку солнечные лучи можно считать
параллельными .
В случае, когда прямая р перпендикулярна плоскости α
называется ортогональным проектированием. В этом
случае проекцией Х1 точки Х, не лежащей в плоскости α,
на эту плоскость является основание перпендикуляра,
проведенного из точки Х на плоскость α.
ИЗУЧЕНИИ
ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ
В СТАРШЕЙ ШКОЛЕ



















 Число и цифра 3
Число и цифра 3 Моделирование устойчивого развития экономических систем
Моделирование устойчивого развития экономических систем Определители 2,3,n порядка. Тема 1
Определители 2,3,n порядка. Тема 1 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Математическая модель
Математическая модель Как учились математике дети в прошлые времена Предметное исследование Гулк Екатерины Ученицы 5 аш класса Гимназии №41 Имени Э.
Как учились математике дети в прошлые времена Предметное исследование Гулк Екатерины Ученицы 5 аш класса Гимназии №41 Имени Э.  Случайная величина
Случайная величина Решение тригонометрических уравнений
Решение тригонометрических уравнений ЕГО ВЕЛИЧЕСТВО
ЕГО ВЕЛИЧЕСТВО  Точки и прямые
Точки и прямые Возрастание убывание функции Степенная функция Учитель математики Голубкова Елена Юрьевна ГБОУ школа №135 Выборгского района
Возрастание убывание функции Степенная функция Учитель математики Голубкова Елена Юрьевна ГБОУ школа №135 Выборгского района  Исполнители: Лазарев Данил, Обухов Ярослав, ученики 5 «А» класса. Руководители: Батрудинова Л.Г., учитель математики, Мищенк
Исполнители: Лазарев Данил, Обухов Ярослав, ученики 5 «А» класса. Руководители: Батрудинова Л.Г., учитель математики, Мищенк Логарифмическая линия в ЕГЭ - 2011
Логарифмическая линия в ЕГЭ - 2011  Аттестационная работа. Программа внеурочной деятельности учащихся 7 кл. научно-познавательного направления «Модульное оригами»
Аттестационная работа. Программа внеурочной деятельности учащихся 7 кл. научно-познавательного направления «Модульное оригами» Математика и другие науки Учитель математики ГБОУ СОШ №1413 г. Москвы Шумилова Юлия Евгеньевна
Математика и другие науки Учитель математики ГБОУ СОШ №1413 г. Москвы Шумилова Юлия Евгеньевна  Параллельные прямые в архитектуре
Параллельные прямые в архитектуре Производная функции
Производная функции Деление и бриод
Деление и бриод Многочлены. Обобщающий урок - путешествие
Многочлены. Обобщающий урок - путешествие Разложение многочленов на множители с помощью комбинаций различных приёмов
Разложение многочленов на множители с помощью комбинаций различных приёмов Шесть вопросов по планиметрии
Шесть вопросов по планиметрии Решение заданий по материалам ЕГЭ 2012 года. Математика (часть 3)
Решение заданий по материалам ЕГЭ 2012 года. Математика (часть 3) Понятие угла. Радианная мера угла
Понятие угла. Радианная мера угла Сложение обыкновенных дробей. Графический диктант 4. 5 класс
Сложение обыкновенных дробей. Графический диктант 4. 5 класс Параллельность прямых в пространстве
Параллельность прямых в пространстве Математические методы в историческом исследовании. (Лекция 1)
Математические методы в историческом исследовании. (Лекция 1) Перпендикулярность прямой и плоскости (10 класс)
Перпендикулярность прямой и плоскости (10 класс) Презентация на тему Решение задач на разностное и кратное сложение чисел
Презентация на тему Решение задач на разностное и кратное сложение чисел