Случайная величина

Закон распределения случайной величины

Это связь между возможными значениями случайной величины

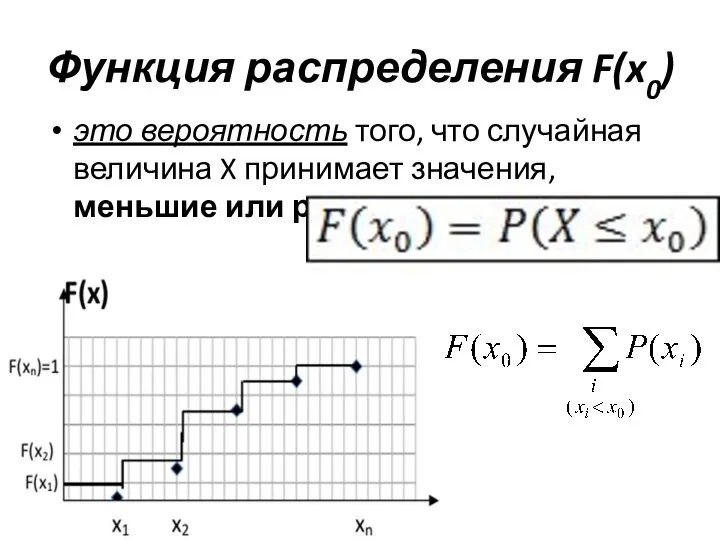
Функция распределения F(x0)

это вероятность того, что случайная величина X принимает значения,

Свойства функции распределения

1). F(x) неубывающая: F(x2)≥F(x1) если x2≥x1
2).F(-∞)=0; F(+∞)=1

Вероятность попадания

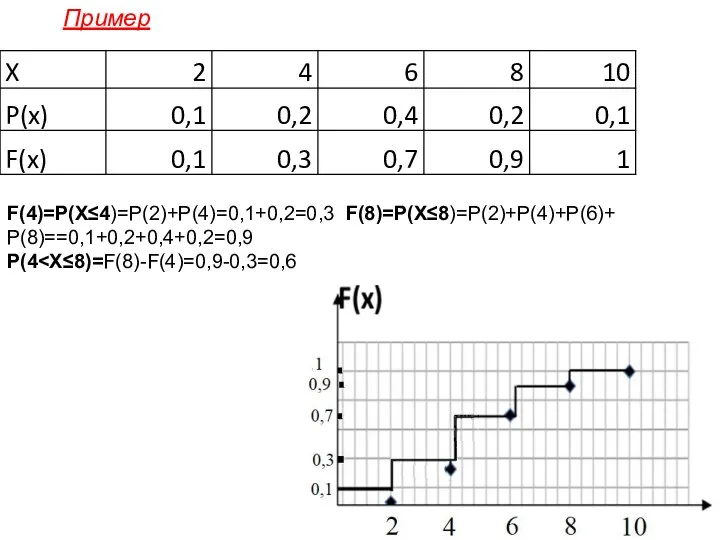
F(4)=P(X≤4)=P(2)+P(4)=0,1+0,2=0,3 F(8)=P(X≤8)=P(2)+P(4)+P(6)+
P(8)==0,1+0,2+0,4+0,2=0,9
P(4

Пример

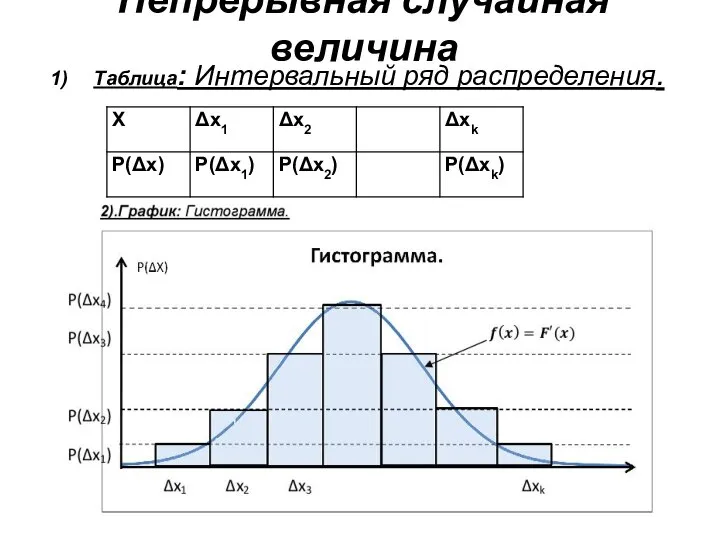
Непрерывная случайная величина

Таблица: Интервальный ряд распределения.

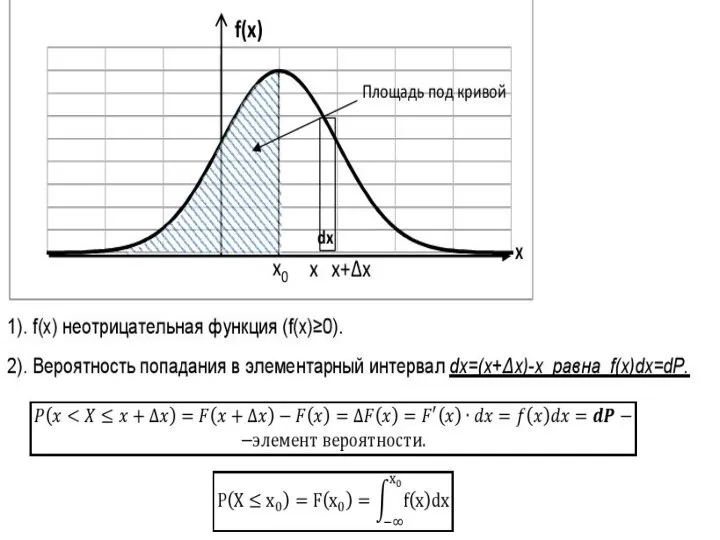
Функция плотности вероятности

Числовые характеристики случайной величины.

Пусть проведено n испытаний, случайная величина приняла

Числовые характеристики случайной величины.

2) Дисперсия (рассеивание). Это математическое ожидание (среднее

Числовые характеристики случайной величины

Если X и Y независимые случайные величины,то

Так как

Законы распределения дискретной случайной величины. Биномиальное распределение

Пусть производится N независимых опытов(бросаем

Биномиальное распределение

Вероятность такой случайной величины вычисляют по формуле
где q=1-p ;

к!=1•2•

Задача господина де Мере

Распределение Пуассона Редкие события

Если количество испытаний  достаточно велико (N), а вероятность  появления

Если в биномиальном распределении зафиксировать k , а N увеличивать таким

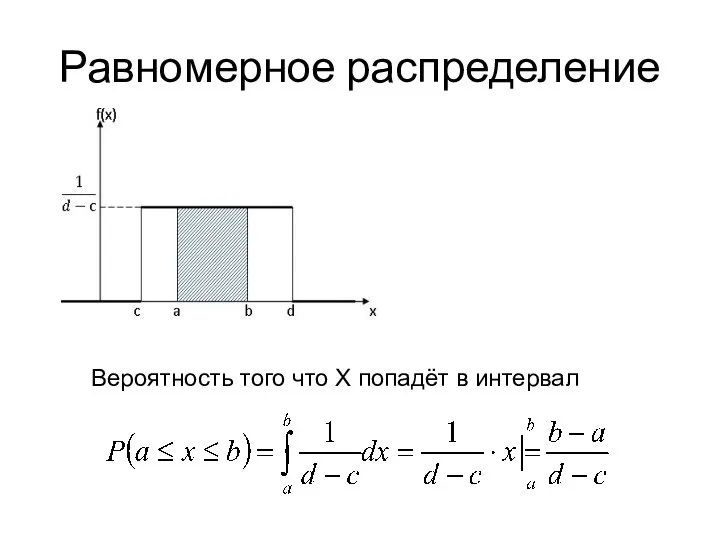
Основные законы распределения непрерывной случайной величины

1.Равномерное или прямоугольное распределение.
Случайная величина называется

Равномерное распределение

Вероятность того что X попадёт в интервал

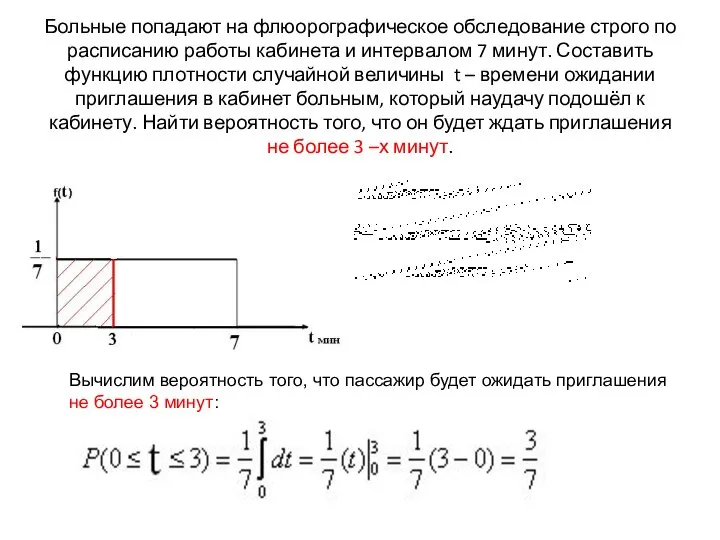
Больные попадают на флюорографическое обследование строго по расписанию работы кабинета и

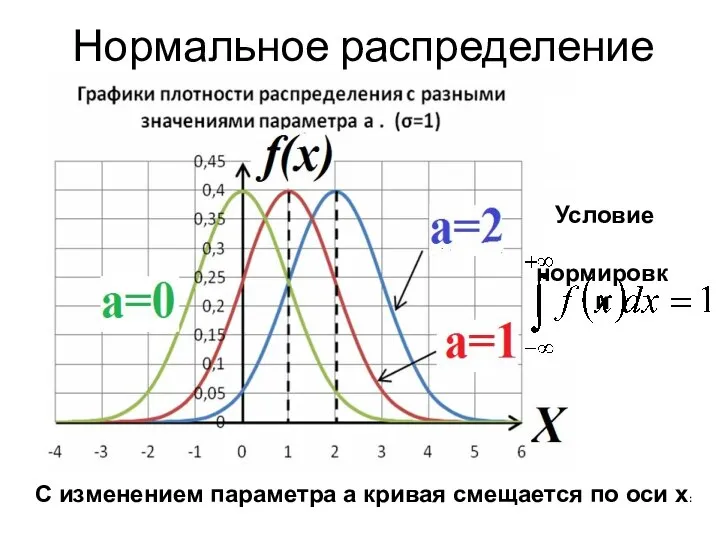
Нормальный закон распределения или распределение Гаусса

a и σ

Нормальное распределение

С изменением параметра а кривая смещается по оси

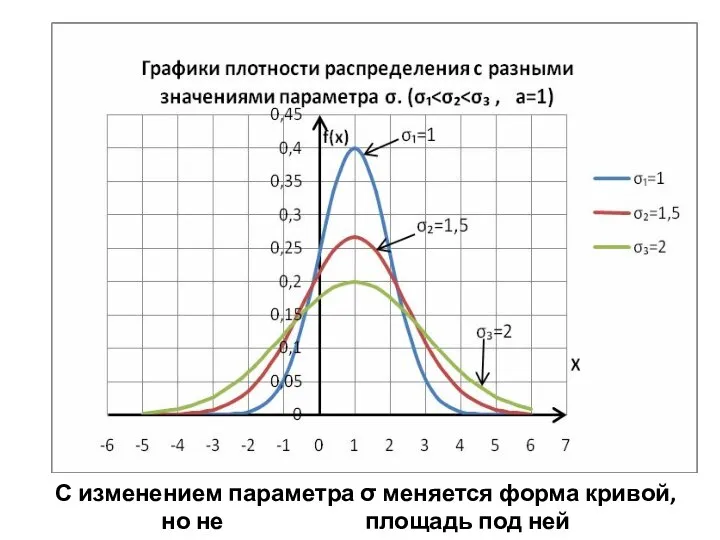
С изменением параметра σ меняется форма кривой, но не площадь под

Параметры нормального распределения

математическое ожидание

дисперсия.

– среднее квадратическое отклонение.

Нормальная функция распределения
Введём замену переменной:

Свойства функции Ф(t)

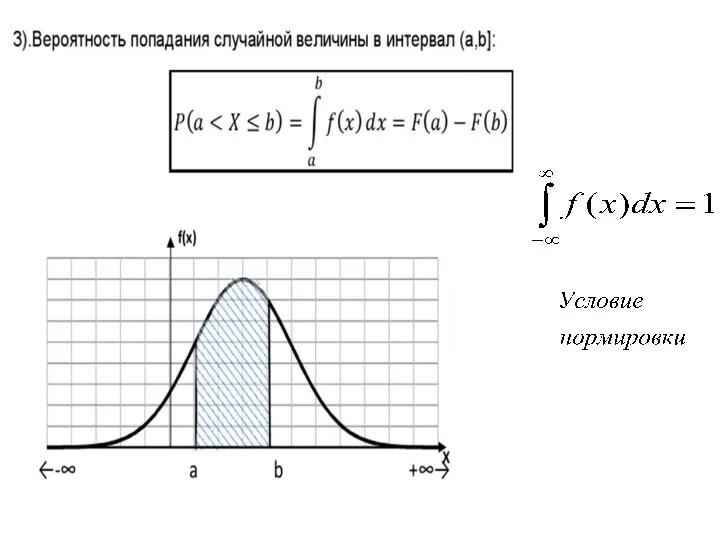
Вероятность попадания значений случайной величины в интервал [a.b]

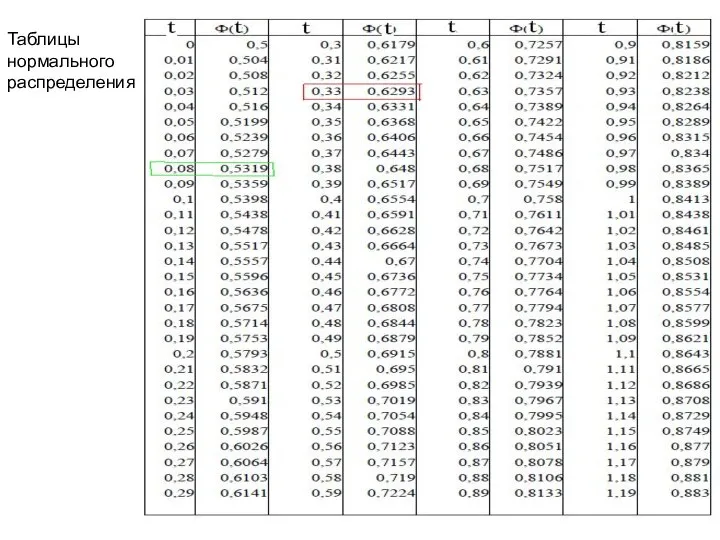
Таблицы нормального распределения

Таблицы
нормального
распределения

Пример 1

Случайная величина распределена по нормальному закону. Параметры распределения:a=4, σ=3. Найти

Пример 2

Случайная величина распределена по нормально-му закону. Параметры распределения:a=4,
Чему равно

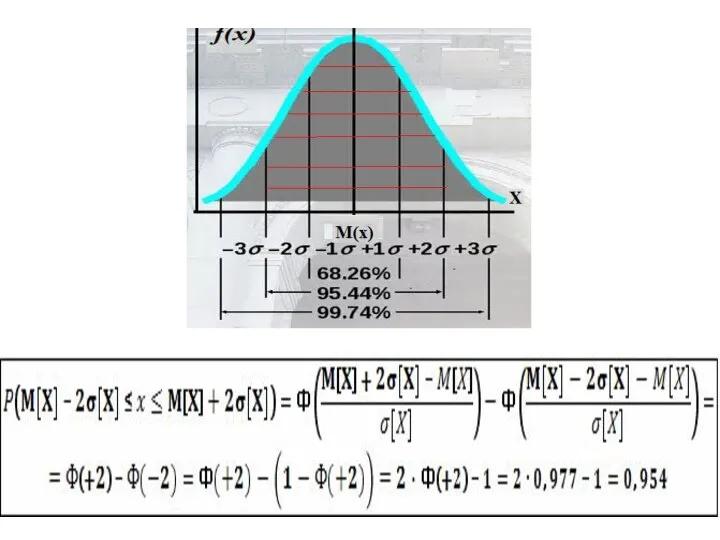
Правило 3-х сигм

Математическая статистика.

Статистическая совокупность – это множество объектов, обладающих общими признаками, которые

Основные задачи, которые стоят перед математической статистикой

Определение закона распределения случайной величины

Сбор экспериментальных данных.

1) Получаем статистический ряд –совокупность числовых данных или выборку

3) Составляем вариационный ряд (статистическое распределение)

Дискретный вариационный ряд это таблица, состоящая

Для непрерывной случайной величины
составляется интервальный вариационный ряд:

Первая строка -

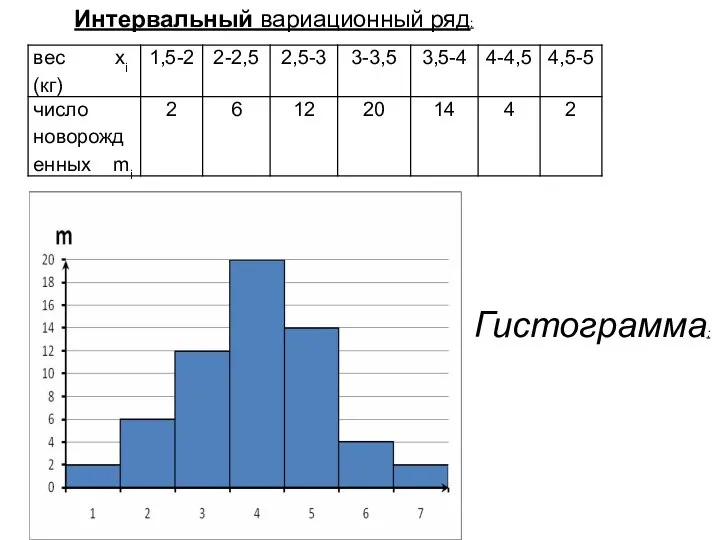
Интервальный вариационный ряд:

Гистограмма:

Статистические характеристики совокупности

Генеральная совокупность (n→∞)
Дисперсия

Выборка (n- конечно)

Математическое ожидание

Среднее арифметическое

Ошибка среднего арифметического

Извлечём из генеральной совокупности N выборок одинакового объёма n,

Интервальные оценки параметров Доверительный интервал

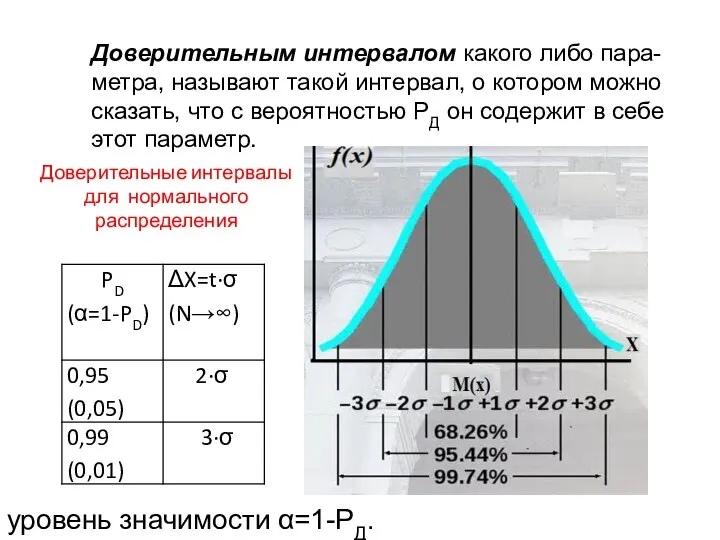
Доверительным интервалом какого либо пара-метра, называют такой интервал, о котором можно

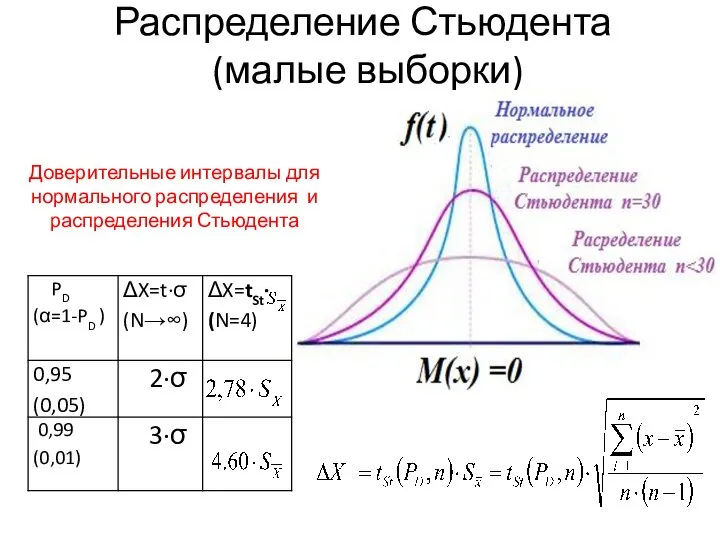
Распределение Стьюдента (малые выборки)

Доверительные интервалы для нормального распределения и распределения Стьюдента

Пример: При определении концентрации белка в растворе были получены следующие результаты

Алгоритм обработки результатов прямых измерений

1) Провести серию измерений, не менее трех

Алгоритм обработки результатов прямых измерений

4) Найти систематическую ошибку.
а). если указан класс

Алгоритм обработки результатов прямых измерений

6) Записать окончательный результат: .

7) Кроме абсолютной