Содержание
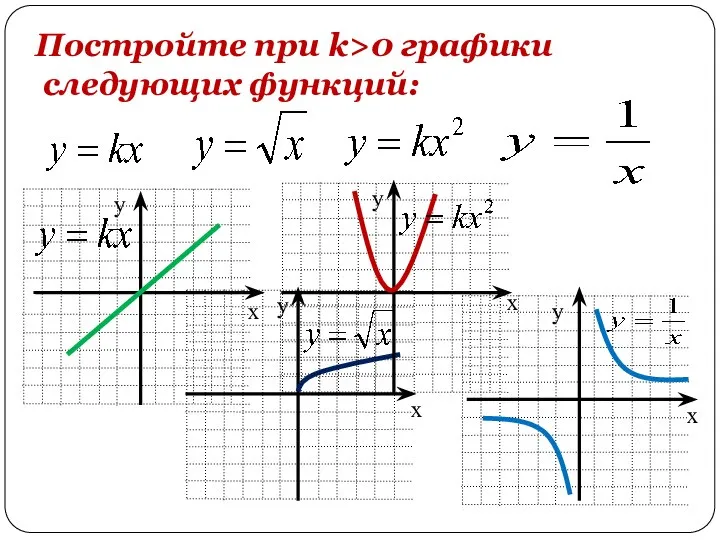
- 2. Постройте при k>0 графики следующих функций:
- 3. Свойства числовых неравенств. Если a>b и b>c, то a>c. Если a>b, то a+c>b+c. Если a>b и
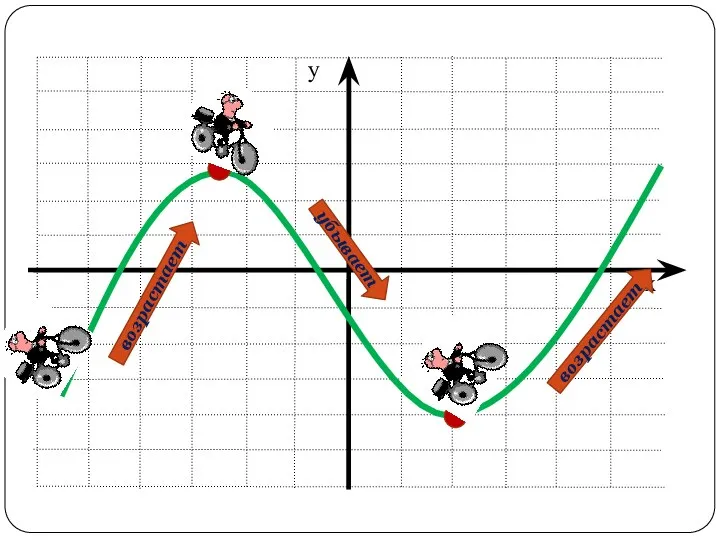
- 4. возрастает убывает возрастает
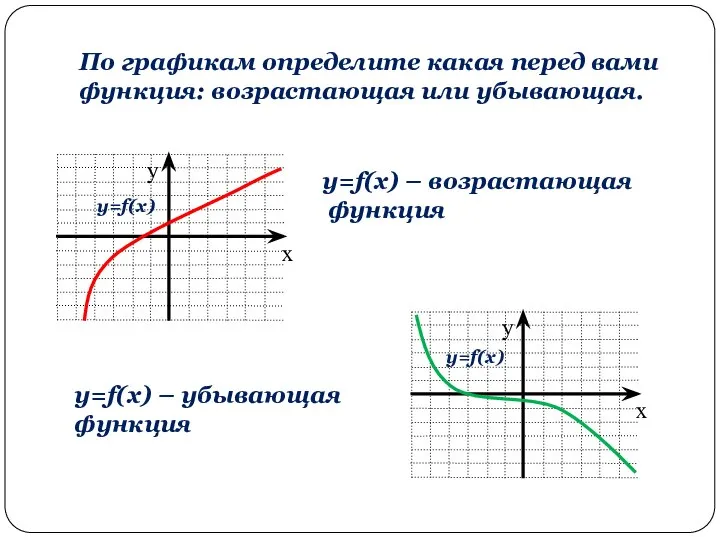
- 5. По графикам определите какая перед вами функция: возрастающая или убывающая. y=f(x) – возрастающая функция y=f(x) –
- 6. Определения понятий возрастания и убывания функций. Определение 1. Функцию y=f(x) называют возрастающей на промежутке Х, если
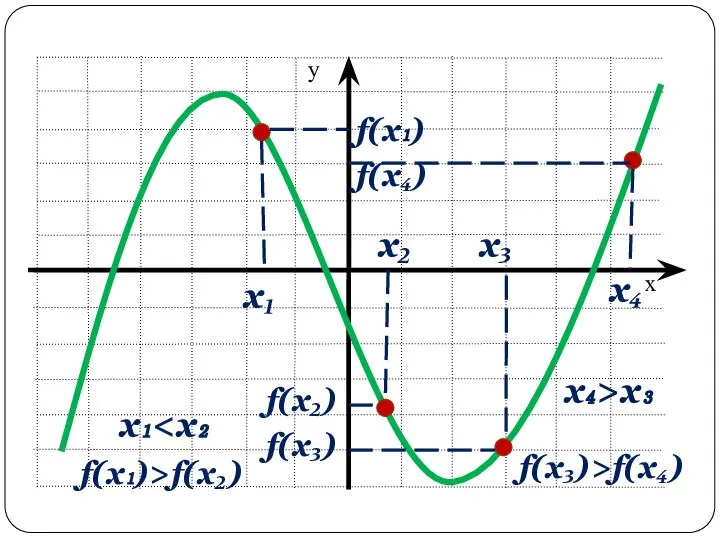
- 7. х₁ х₂ х₁ f(x₁) f(x₂) f(x₁)>f(x₂) х₃ х₄ f(x₄) f(x₃) х₄>x₃ f(x₃)>f(x₄)
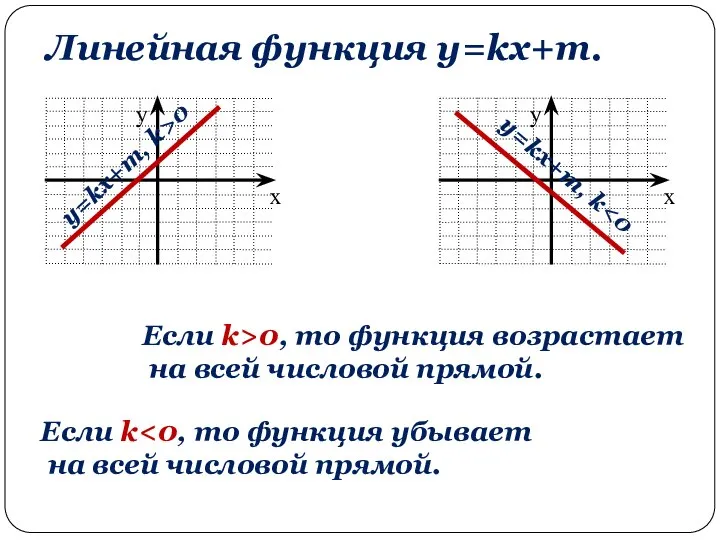
- 8. Линейная функция y=kx+m. y=kx+m, k>0 y=kx+m, k Если k>0, то функция возрастает на всей числовой прямой.
- 9. Доказательство: Пусть f(x)=kx+m. Если х₁ 0, то kx₁ Если kx₁ Значит f(x₁) Из неравенства х₁ Это
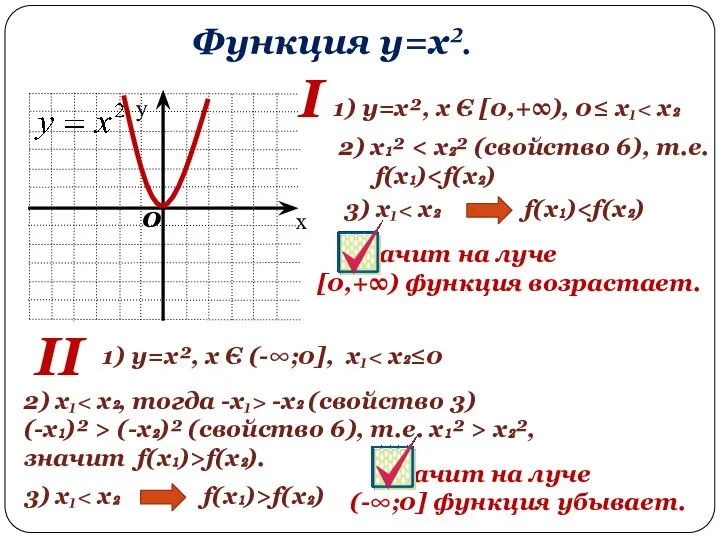
- 10. Функция y=x². 0 1) y=x², х Є [0,+∞), 0≤ х₁ 2) х₁² f(x₁) 3) х₁ Значит
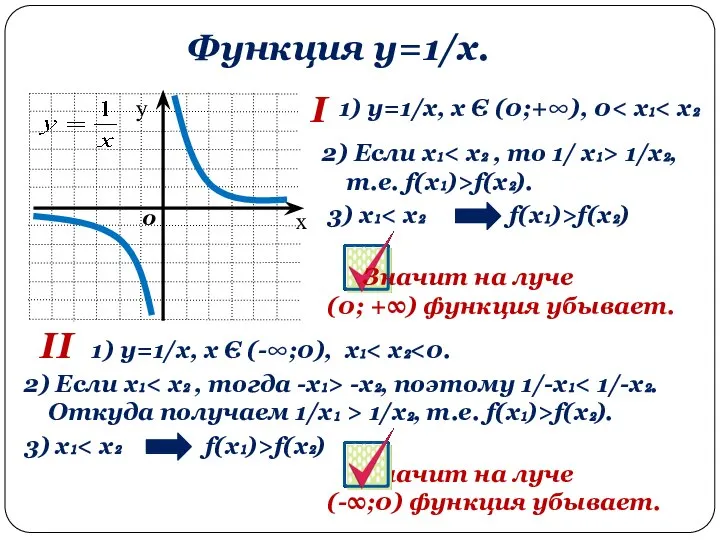
- 11. Функция y=1/x. 0 I 1) y=1/x, x Є (0;+∞), 0 2) Если х₁ -х₂, поэтому 1/-х₁
- 12. Термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция. Исследование функции на возрастание и убывание
- 13. Исследовать на монотонность (х>0) (х>0)
- 15. Скачать презентацию





 Презентация на тему Неравенства и их решения
Презентация на тему Неравенства и их решения  «Таблица умножения и деления». 2 класс
«Таблица умножения и деления». 2 класс Взаимно обратные числа
Взаимно обратные числа Делимость чисел
Делимость чисел Прикладная математика. Системы уравнений
Прикладная математика. Системы уравнений Кластеризация. Понятие кластеризации
Кластеризация. Понятие кластеризации Устный счёт
Устный счёт Комплексные чертежи линий
Комплексные чертежи линий Геометрические фигуры в национальных костюмах” и “Красота природы в геометрии”
Геометрические фигуры в национальных костюмах” и “Красота природы в геометрии” Квадратные уравнения
Квадратные уравнения Геометрия древесного ствола
Геометрия древесного ствола Математические основы манипулирования реляционными данными
Математические основы манипулирования реляционными данными Нахождение угла треугольника
Нахождение угла треугольника Таблица умножения и деления на 4
Таблица умножения и деления на 4 Частные производные
Частные производные Решение неравенств с одной переменной
Решение неравенств с одной переменной Решение систем линейных уравнений методом алгебраического сложения
Решение систем линейных уравнений методом алгебраического сложения Памятка по оформлению краткой записи к задачам (1 класс)
Памятка по оформлению краткой записи к задачам (1 класс) Приведение дробей к новому знаменателю
Приведение дробей к новому знаменателю Элементы учебно-исследовательской деятельности на уроках математики в гуманитарных классах
Элементы учебно-исследовательской деятельности на уроках математики в гуманитарных классах Мнемонические приемы при решении задания ЕГЭ №13
Мнемонические приемы при решении задания ЕГЭ №13 Математическая игра
Математическая игра ЧТО? ГДЕ? КОГДА? Игра 10 класс
ЧТО? ГДЕ? КОГДА? Игра 10 класс  Сравнения группы предметов по количеству: больше, меньше, столько же. Старшая группа
Сравнения группы предметов по количеству: больше, меньше, столько же. Старшая группа Решение заданий ЕГЭ В6 (часть 1)
Решение заданий ЕГЭ В6 (часть 1) «Прогрессия. Применение формул алгебраической и геометрической прогрессии в электронных таблицах» 9 класс
«Прогрессия. Применение формул алгебраической и геометрической прогрессии в электронных таблицах» 9 класс Презентация по математике "Сравнение отрезков и углов" - скачать бесплатно
Презентация по математике "Сравнение отрезков и углов" - скачать бесплатно Сумма углов треугольника
Сумма углов треугольника