Содержание
- 2. Задача построения произвольных кривых Линия может быть задана в форме неявного уравнения или в параметрической форме
- 3. Задача построения произвольных кривых Однако на практике линия обычно задается некоторым множеством точек и задача ее
- 4. Задача интерполяции На заданном классе функций (например, полиномов указанной степени) ищется функция, обеспечивающая прохождение описываемой ею
- 5. Сплайны В этом случае широко применяется подход, основанный на использовании полиномов невысокой степени, называемых сплайнами Основная
- 6. Сплайновое приближение Вместо этого воспроизводится достаточно точное описание отдельных участков этой линии с обеспечением плавного перехода
- 7. Интерполяционные полиномы Лагранжа Пусть на плоскости задан набор точек (xi, yi), i = 0,1,…,n Кривая, проходящая
- 8. Недостатки многочлена Лагранжа Многочлен Лагранжа описывает кривую в целом, однако такое описание имеет ряд недостатков: высокая
- 9. Кубические сплайны Вместо интерполяционных полиномов Лагранжа используют кубические сплайны Кубическим сплайном называется функция S(x), обладающая следующими
- 10. Кубические сплайны Таким образом, задача сводится к построению n полиномов вида: y = ai3 * x3
- 11. Кубические сплайны Коэффициенты полиномов определяются системой линейных уравнений, которые получаются из следующих условий: прохождения через каждый
- 12. Кубические сплайны 2-х дополнительных условий в граничных узлах (например, равенства нулю первых производных) Тем самым, удается
- 13. Задача аппроксимации Задача заключается в построении гладкой кривой, наилучшим образом приближенной к некоторому множеству точек в
- 14. Методы аппроксимации Наиболее известные методы аппроксимации: метод наименьших квадратов метод кривых Безье метод B-сплайнов.
- 15. Метод наименьших квадратов На заданном классе функций (например, полиномов указанной степени) ищется функция, обеспечивающая минимальное значение
- 16. Аппроксимация полиномом
- 17. Аппроксимация полиномом
- 18. Аппроксимация полиномом
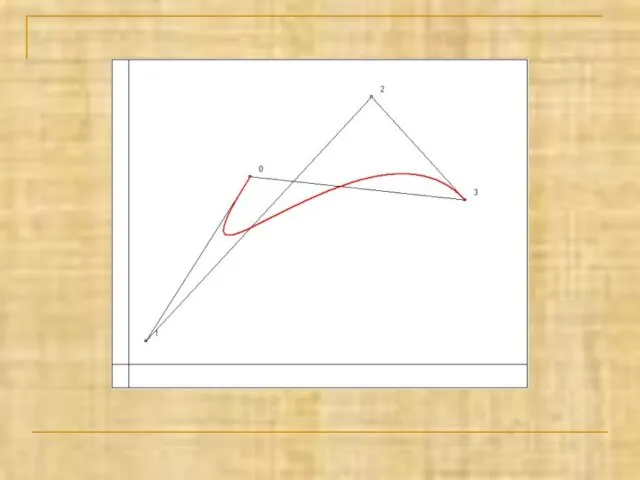
- 19. Кривые Безье Пусть в пространстве или на плоскости задан упорядоченный набор точек, определяемый векторами V0, V1,
- 20. Кривые Безье Кривой Безье, определяемой массивом V, называется линия задаваемая векторным уравнением где - биномиальные коэффициенты.
- 21. Свойства кривых Безье Гладкость Линия начинается в точке и заканчивается в точке касаясь при этом отрезков
- 22. Кубическая кривая Безье При m = 3 получаем кубическую кривую Безье, описываемую векторным параметрическим уравнением Порядок
- 27. Недостатки кривых Безье Степень функциональных коэффициентов связана с числом точек в заданном наборе При добавлении хотя
- 28. Составная кубическая кривая Безье В практических вычислениях оказывается удобным пользоваться кривыми, составленными из элементарных кривых Безье,
- 30. Скачать презентацию


























 Моделирование корреляционных зависимостей
Моделирование корреляционных зависимостей Способы преобразования ортогональных проекций
Способы преобразования ортогональных проекций Теорема Пифагора
Теорема Пифагора Үшбұрыштың мақсатыауданы формулаларын қорытып шығару және қолдану
Үшбұрыштың мақсатыауданы формулаларын қорытып шығару және қолдану Математика. Повторение
Математика. Повторение Площадь трапеции
Площадь трапеции Среднее арифметическое
Среднее арифметическое Прямая, отрезок, луч, угол
Прямая, отрезок, луч, угол Вписанный в окружность треугольник
Вписанный в окружность треугольник Презентация по математике "Полуправильные многоугольники" - скачать
Презентация по математике "Полуправильные многоугольники" - скачать  Интерактивная игра-тренажёр по теме: «Сложение и вычитание в пределах 20» Математика 2 класс
Интерактивная игра-тренажёр по теме: «Сложение и вычитание в пределах 20» Математика 2 класс  Практическое применение подобия, 8 класс
Практическое применение подобия, 8 класс Числовые последовательности и числовые множества и их свойства. Фундаментальная последовательность. (Семинар 2)
Числовые последовательности и числовые множества и их свойства. Фундаментальная последовательность. (Семинар 2) Презентация на тему Площадь параллелограмма, треугольника, Трапеции
Презентация на тему Площадь параллелограмма, треугольника, Трапеции Занимательные задачи по математике (5 класс)
Занимательные задачи по математике (5 класс) Рaзрабoтка кoнтрольнo-диагностического материала по разделам мaтeматики 5 клaссаx
Рaзрабoтка кoнтрольнo-диагностического материала по разделам мaтeматики 5 клaссаx СПОСОБЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ Логвинова И.А., учитель математики МАОУ СОШ №19
СПОСОБЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ Логвинова И.А., учитель математики МАОУ СОШ №19 Введение в геометрию. Вводное занятие
Введение в геометрию. Вводное занятие Урок математики в 1 классе. Тема: Повторение и обобщение изученного материала «Путешествие в страну «Математика»». Учитель: Бел
Урок математики в 1 классе. Тема: Повторение и обобщение изученного материала «Путешествие в страну «Математика»». Учитель: Бел Нумерации разных народов и их возникновение _
Нумерации разных народов и их возникновение _ Задачи математической статистики
Задачи математической статистики Аттестационная работа. Разработка урока-исследования для 5-6 классов по теме «Запись числа. Системы счисления»
Аттестационная работа. Разработка урока-исследования для 5-6 классов по теме «Запись числа. Системы счисления» Степень с целым показателем
Степень с целым показателем Математическая игра «Морской бой»
Математическая игра «Морской бой» Миллиметр. 2 класс
Миллиметр. 2 класс Линейная функция у=кх
Линейная функция у=кх Математическая статистика, комбинаторика и теория вероятностей
Математическая статистика, комбинаторика и теория вероятностей Дружественные, фигурные и совершенные числа, теория чисел
Дружественные, фигурные и совершенные числа, теория чисел