Содержание
- 2. Учебные цели: Ознакомить обучающихся со структурой дисциплины «Высшая математика», ее целями, а также задачами, ставящимися при
- 3. Учебные вопросы: Матрица. 2. Виды матриц. Операции над матрицами. 3. Понятие определителя. Свойства определителей.
- 4. ПЕРВЫЙ УЧЕБНЫЙ ВОПРОС МАТРИЦА
- 5. Одной из характерных особенностей развития современного общества является широкое применение математических методов и компьютерной техники в
- 6. Математика оказывает существенную помощь в изучении явлений и процессов, встречающихся как в различных учениях о природе,
- 7. Мы начинаем курс высшей математики с изучения одного из его основных разделов – линейной алгебры. Далее
- 8. В высшей математике используют достаточно простую, а главное, компактную форму записи и решения задач, а именно,
- 9. Числовой матрицей или просто матрицей называется любая прямоугольная таблица чисел. Горизонтальные ряды матрицы называются строками, а
- 10. Записывают матрицы в круглых скобках, не ставя между элементами никаких знаков. При необходимости, за матрицей внизу
- 11. Например, матрица размерности m×n: Иногда для обозначения матрицы используют двойные вертикальные линии. (2) Матрица (2) является
- 12. Рассмотрим матрицу системы уравнений вида: Две матрицы А и В одной размерности называются равными, если у
- 13. Вопрос 2. Виды матриц. Операции над матрицами Матрица называется нулевой (или нуль-матрицей), если все ее элементы
- 14. ВТОРОЙ УЧЕБНЫЙ ВОПРОС ВИДЫ МАТРИЦ. ОПЕРАЦИИ НАД МАТРИЦАМИ
- 15. Матрица, у которой число строк равно числу столбцов, называется квадратной. Число строк, а, следовательно, и число
- 16. Квадратная матрица называется матрицей треугольного вида, если все ее элементы, расположенные под (или над) одной из
- 17. Операции над матрицами Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из
- 18. 1.Умножение матрицы на число Произведением матрицы А на число α (или числа α на матрицу А)
- 19. Следствие. Общий множитель всех элементов матрицы можно вынести за знак матрицы. Например, 2. Сложение матриц Суммой
- 20. Пример 2.1 3. Вычитание матриц Вычитание можно определить через рассмотренные ранее операции: А – В =
- 21. 4.Умножение матриц Произведение матриц имеет место только для матриц определенных размерностей. Матрицу А можно умножить на
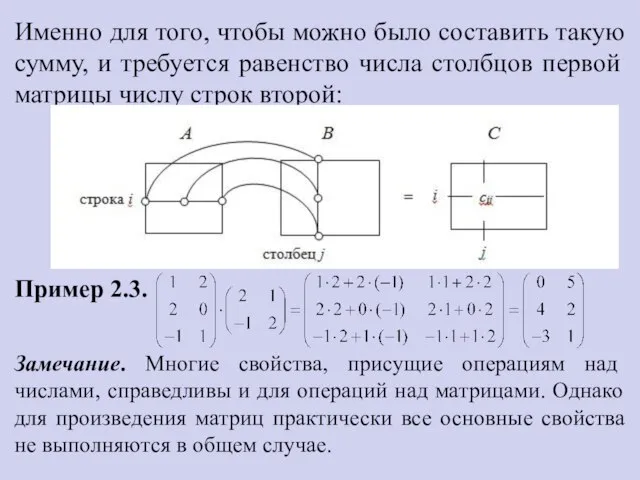
- 22. Именно для того, чтобы можно было составить такую сумму, и требуется равенство числа столбцов первой матрицы
- 23. Особенности умножения матриц 1. Для произвольных матриц АВ≠ВА. Так как возможно, что произведение АВ существует, а
- 24. Однако существует матрица, для которой переместительный закон умножения выполняется. Если матрица А – квадратная матрица порядка
- 25. 2. Если произведение матриц равно нулю, то совсем не обязательно, чтобы какой-либо из сомножителей был нулевой
- 26. - прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то
- 27. Матрица, полученная из данной матрицы А заменой каждой ее строки столбцом с тем же номером, называется
- 28. Таким образом, мы рассмотрели основные понятия теории матриц, которыми будем пользоваться в дальнейшем. Изучили различные виды
- 29. ТРЕТИЙ УЧЕБНЫЙ ВОПРОС ПОНЯТИЕ ОПРЕДЕЛЕИТЕЛЯ. СВОЙСТВА ОПРЕДЕЛЕИТЕЛЕЙ
- 30. С понятием матрицы тесно связано понятие определителя. Определители широко применяются в линейной и общей алгебре, в
- 31. Теория определителей возникла в XVI веке и развита более полно в XVII веке в связи с
- 32. Понятие определителя. Квадратной матрице А порядка n можно сопоставить число det A (или |А| или Δ),
- 33. 2. n=2. Определителем матрицы второго порядка называется число, определяемое по формуле: |А| = Определитель второго порядка
- 34. 3. n=3. Определителем матрицы третьего порядка называется число, определяемое по формуле: Это число представляет собой алгебраическую
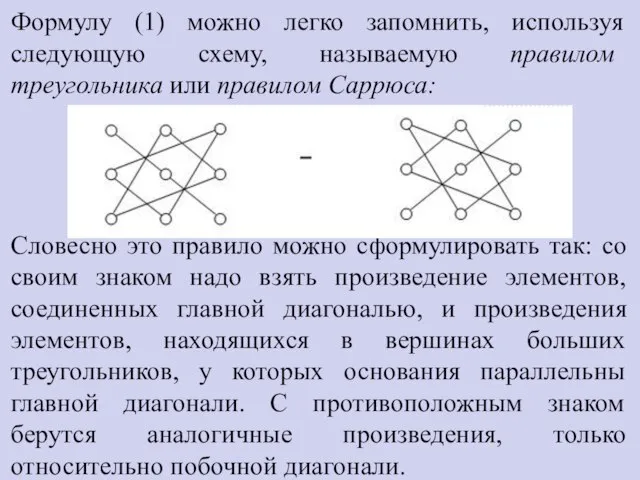
- 35. Формулу (1) можно легко запомнить, используя следующую схему, называемую правилом треугольника или правилом Саррюса: Словесно это
- 36. Пример 3.1 |А| = = 16+6+0−0−2−0 = 20. Вычисление определителя матрицы n-го порядка связано с понятиями
- 37. Пусть дана квадратная матрица n-го порядка. Минором Мij некоторого элемента аij определителя n-го порядка называется определитель
- 38. Например, для элементов а11 и а12 матрицы А = миноры М11 = М12 = а алгебраические
- 39. Свойства определителей Вычисление определителей (особенно высших порядков) довольно часто упрощается, если воспользоваться их свойствами. 1. Основное
- 40. Пример 3.1. Вычислим определитель матрицы А с помощью разложения по первой строке и сверим результат с
- 41. Замечание 2: с помощью разложения по строке или столбцу любой определитель n-го порядка можно свести к
- 42. 2. Если строка или столбец определителя состоит из нулей, то определитель равен нулю. Доказательство. Для доказательства
- 43. 4. Общий множитель элементов любого ряда можно вынести за знак определителя. Доказательство этого свойства, как и
- 44. 5. Определитель, имеющий два одинаковых ряда, равен нулю. Доказательство. В самом деле, при перестановке двух одинаковых
- 45. 7. Величина определителя не изменится, если все строки и столбцы поменять местами (другими словами, при транспонировании
- 46. 8. Если каждый элемент n-го столбца (n-й строки) определителя представляет собой сумму двух слагаемых, то определитель
- 47. 9. Величина определителя не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженного
- 48. 10. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
- 49. Заменим в определителе Δ первый столбец на произвольные числа h1, h2, h3. Алгебраическими дополнениями элементов h1,
- 50. Пример 3.2. Используя свойства, вычислить определитель: Решение. Видим, что 1-й и 3-й столбцы определителя пропорциональны. По
- 51. Пример 2.3. Используя свойства, вычислить определитель: Решение. Вычислим данный определитель разложением по элементам 3-го столбца. Руководствуясь
- 53. Скачать презентацию
















































 Различные способы решения тригонометрических неравенств
Различные способы решения тригонометрических неравенств Решение показательных уравнений и неравенств
Решение показательных уравнений и неравенств Лозунговый шифр
Лозунговый шифр Решение задач. Подготовка к ЕГЭ
Решение задач. Подготовка к ЕГЭ Кластерный анализ
Кластерный анализ Аттестационная работа. Проектная работа «Культура устного счета в изучении математики в России»
Аттестационная работа. Проектная работа «Культура устного счета в изучении математики в России»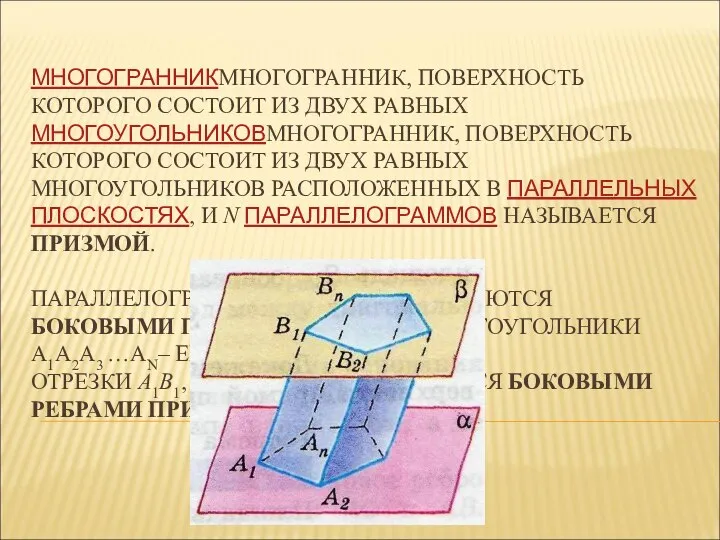 Призма. Виды призмы. Свойства призмы
Призма. Виды призмы. Свойства призмы Лекция 3.1. Криволинейные интегралы. Определение криволинейных интегралов
Лекция 3.1. Криволинейные интегралы. Определение криволинейных интегралов Математический калейдоскоп: www.themegallery.com
Математический калейдоскоп: www.themegallery.com Презентация по математике "Решение задач" - скачать бесплатно
Презентация по математике "Решение задач" - скачать бесплатно Округление натуральных чисел
Округление натуральных чисел Новые типы обратных связей в системах автоматического управления
Новые типы обратных связей в системах автоматического управления 5 класс.
5 класс.  Генеральная совокупность и выборка
Генеральная совокупность и выборка Интерактивная дидактическая игра «Состав чисел до 10». Математика, 1 класс
Интерактивная дидактическая игра «Состав чисел до 10». Математика, 1 класс Отношение. Пропорция
Отношение. Пропорция Виды графиков линейной функции
Виды графиков линейной функции Методы оптимизации объектов
Методы оптимизации объектов Ребусы по математике
Ребусы по математике Математические отношения
Математические отношения Построение графика функции
Построение графика функции Решение уравнений и неравенств, содержащих переменную под знаком модуля
Решение уравнений и неравенств, содержащих переменную под знаком модуля Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Теорема о трёх перпендикулярах
Теорема о трёх перпендикулярах Исчисление предикатов
Исчисление предикатов Аттестационная работа. Решение сложных задач по математике
Аттестационная работа. Решение сложных задач по математике Числовые и алгебраические выражения
Числовые и алгебраические выражения Роль диагностики в обучении математи
Роль диагностики в обучении математи