Содержание
- 2. Непрерывное распределение, которое занимает наиболее важное положение в теории и практике статистики − распределение Гаусса, или
- 3. 3) Является пределом для других ЗР при некотором n → ∞ (биномиальный при ∞ числе испытаний)
- 4. Ошибки измерений часто нормальны (такие распределения обнаружили астрономы в 18 веке) В статистике − распределение выборочного
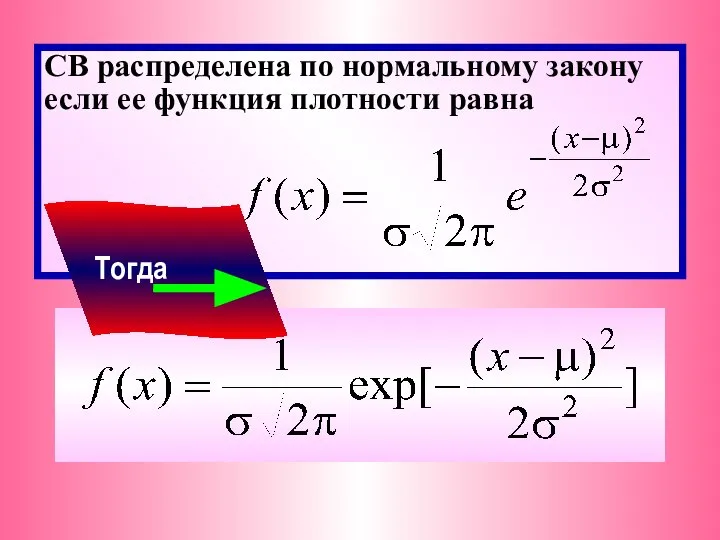
- 5. СВ распределена по нормальному закону если ее функция плотности равна Тогда
- 6. Функция распределения нормальной величины определяется как Параметры μ и σ2 − матожидание и дисперсия Это двухпараметрический
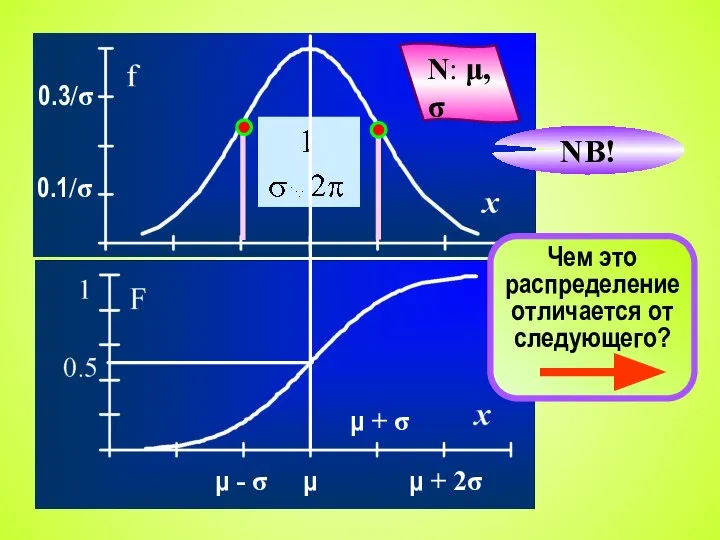
- 7. N: μ, σ Чем это распределение отличается от следующего? NB!
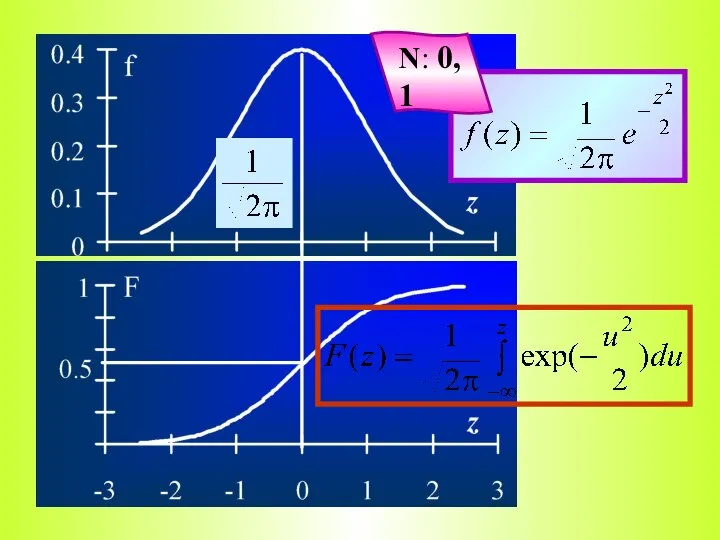
- 8. N: 0, 1
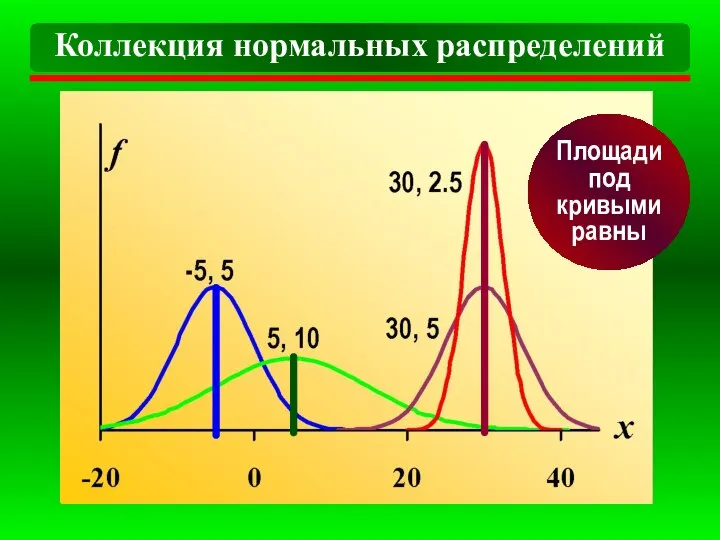
- 9. Коллекция нормальных распределений Площади под кривыми равны
- 10. Различия: ∙ привязаны к разным точкам μ числовой оси ∙ чем площадь под кривой вблизи μ,
- 11. Стандартный нормальный закон Будучи стандартом для других ЗР, нормальное распределение имеет свой собственный стандарт Это N:
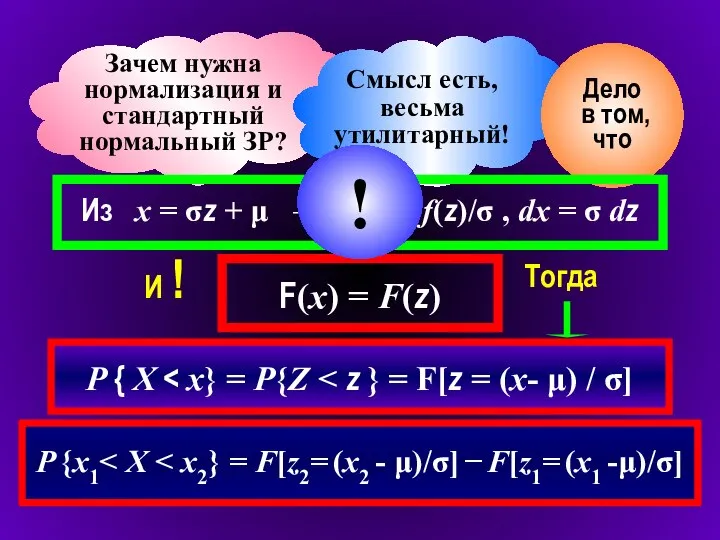
- 12. Зачем нужна нормализация и стандартный нормальный ЗР? Смысл есть, весьма утилитарный! Дело в том, что Из
- 13. Вместо расчета интегралов всякий раз для разных μ и σ, можно использовать раз и навсегда рассчитанные
- 14. У нее следующие свойства: Φ(0) = 0; Φ(∞) = 0.5; это нечетная функция, Φ(− z) =
- 15. Удобное практическое правило Вероятность того, что нормальная величина примет значение из некоторого интервала равна разности значений
- 16. P{150 Φ[z2 = (200-160)/20=2] − Φ[z1 =(150-160)/20=-0.5] = Φ(2) + Φ(0.5) = 0.4472 + 0.1915 =
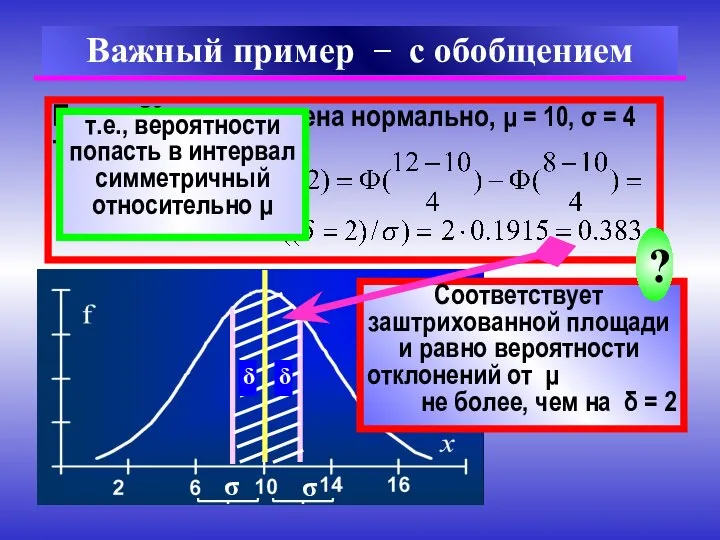
- 17. Пусть X распределена нормально, μ = 10, σ = 4 Тогда Важный пример − с обобщением
- 18. Общее правило Вероятность того, что (при измерении, управлении, производстве …) отклонение от μ (неизвестного истинного, предписанного
- 19. Очевидно! риск выйти за нормативные границы шансы отклонений, превышающих заданное δ определяет !!! !
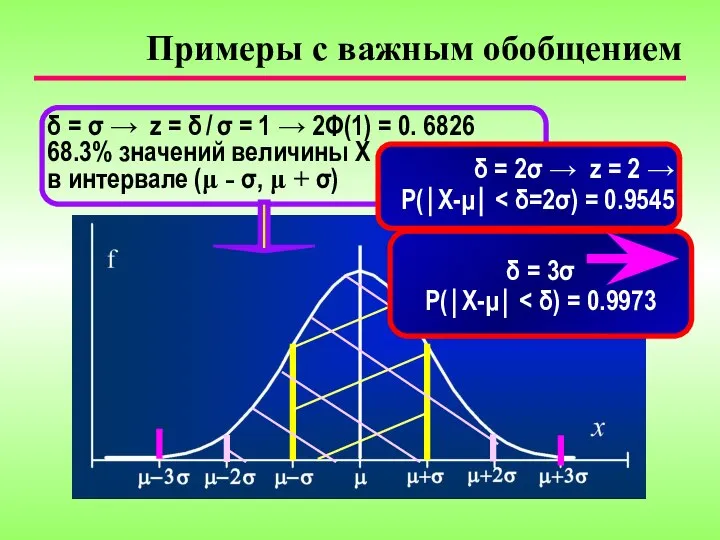
- 20. Примеры с важным обобщением δ = σ → z = δ / σ = 1 →
- 21. 99.7% значений нормально распределенной величины попадают в интервал (μ ± 3σ) Тогда P(⏐X−μ⏐ > 3σ) =
- 23. Скачать презентацию









![P{150 Φ[z2 = (200-160)/20=2] − Φ[z1 =(150-160)/20=-0.5] = Φ(2) + Φ(0.5)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1467511/slide-15.jpg)



 Вектора. Пространства. Скалярное, векторное и смешанное произведение векторов
Вектора. Пространства. Скалярное, векторное и смешанное произведение векторов Множества. Элементы множества
Множества. Элементы множества Задача по финансовой математике
Задача по финансовой математике Параллельные прямые
Параллельные прямые Решение задач на сложение и вычитание смешанных чисел 5 класс Учебник Дорофеева.
Решение задач на сложение и вычитание смешанных чисел 5 класс Учебник Дорофеева. Квадратное уравнение Работу выполнила преподаватель математики Рунгинской средней общеобразовательной школы Комиссарова Л.И.
Квадратное уравнение Работу выполнила преподаватель математики Рунгинской средней общеобразовательной школы Комиссарова Л.И. Презентация по математике "Тест по математике за первое полугодие для 1 класса" - скачать
Презентация по математике "Тест по математике за первое полугодие для 1 класса" - скачать  Дифференциальное исчисление
Дифференциальное исчисление Медиана, как статистическая характеристика
Медиана, как статистическая характеристика Счастливый случай. Математическая игра
Счастливый случай. Математическая игра «Веселый счет» (Счет в прямом и обратном порядке в пределах 10)
«Веселый счет» (Счет в прямом и обратном порядке в пределах 10) Транспортная задача. (Лекции 10,11)
Транспортная задача. (Лекции 10,11) Әйләнә озынлыгы. Түгәрәк мәйданы
Әйләнә озынлыгы. Түгәрәк мәйданы Эйлеровы графы. Гамильтоновы графы
Эйлеровы графы. Гамильтоновы графы Геометрические фигуры вокруг нас
Геометрические фигуры вокруг нас Числовая окружность
Числовая окружность Формулы приведения для тупых углов
Формулы приведения для тупых углов Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Числовые последовательности. 9 класс
Числовые последовательности. 9 класс Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Геометрические загадки
Геометрические загадки Презентация на тему Решение неравенств
Презентация на тему Решение неравенств  Вычисления в MATLAB
Вычисления в MATLAB Шкалы. Основные понятия
Шкалы. Основные понятия Аттестационная работа. Проектные уроки по математике
Аттестационная работа. Проектные уроки по математике Аттестационная работа. Рабочая программа Юный шахматист
Аттестационная работа. Рабочая программа Юный шахматист Презентация на тему Математика в обществознании
Презентация на тему Математика в обществознании  Сумма углов треугольника ГБОУ СОШ №1358 УЧИТЕЛЬ МАТЕМАТИКИ ЕПИФАНОВА ТАТЬЯНА НИКОЛАЕВНА
Сумма углов треугольника ГБОУ СОШ №1358 УЧИТЕЛЬ МАТЕМАТИКИ ЕПИФАНОВА ТАТЬЯНА НИКОЛАЕВНА