Основные понятия математической статистики. (Лекция 3)

Июль 31, 2022

Главная
Математика
Основные понятия математической статистики. (Лекция 3)

Содержание

2. Основные понятия математической статистики. Математическая статистика – это раздел математики о методах регистрации, систематизации и анализа
3. Генеральная совокупность – это совокупность всех объектов, которые имеют типичную характеристику или признак. Это все возможные
4. Основные задачи, которые стоят перед математической статистикой: 1. Определение закона распределения случайной величины по имеющимся статистическим
5. Схема предварительной обработки экспериментальных данных. 1). Сбор экспериментальных данных. Чтобы определить закон распределения случайной величины, нужно
6. Пример: При измерении частоты пульса у 10 пациентов получены следующие результаты: 90, 110, 65, 80, 90,
7. Схема предварительной обработки экспериментальных данных. 2).Составление вариационного ряда. Вариационный ряд (статистическое распределение) -- это двойной ряд
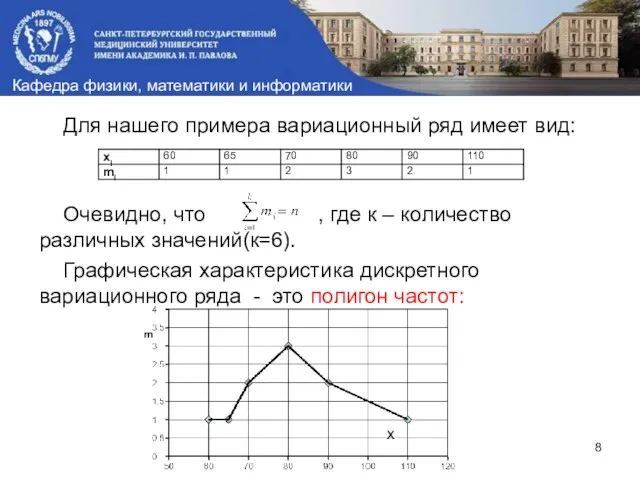
8. Для нашего примера вариационный ряд имеет вид: Очевидно, что , где к – количество различных значений(к=6).
9. Если признак изменяется непрерывно, то составляется интервальный вариационный ряд: В первой строке указываются интервалы изменения признака,
10. Пример.
11. Если признак изменяется непрерывно, то составляется интервальный вариационный ряд: В первой строке указываются интервалы изменения признака,
12. 2. Статистические характеристики совокупности. Математическое ожидание M[X],дисперсия D[X],среднее квадратическое отклонение σ[X] -- это числовые характеристики (параметры),
13. 3. Ошибка среднего арифметического. Извлечём из генеральной совокупности N выборок, тогда их средние арифметические сами будут
14. 4. Доверительный интервал и доверительная вероятность. Истинные значения М[X] и D[X] можно найти по генеральной совокупности,
15. Основная масса случайных величин в биологии и медицине распределена по нормальному закону распределения, следовательно, задав доверительную
16. 5. Распределение Стьюдента. Нормированная случайная величина вычисляется по формуле: Плотность вероятности случайной величины: Где Вn --
18. Скачать презентацию

Слайд 2

Основные понятия математической статистики.
Математическая статистика – это раздел математики о методах

регистрации, систематизации и анализа статистических экспериментальных данных, полученных в результате наблюдения массовых случайных явлений.
Статистическая совокупность – это множество объектов, обладающих общими признаками, которые являются наиболее важными (типичными) для характеристики этих объектов.
Серия измерений какого либо признака совокупности – это совокупность значений случайной величины.
Объём совокупности N –это число членов совокупности.

Слайд 3

Генеральная совокупность – это совокупность всех объектов, которые имеют типичную характеристику

или признак. Это все возможные значения случайной величины.
Выборочная совокупность (выборка) – это отобранная тем или иным способом часть генеральной совокупности.
Из одной генеральной совокупности можно отбирать сколь угодно много выборок, главное, чтобы выборка была репрезентативной (представительной), а для этого элементы выборки должны отбираться случайным образом.
Варианта – это числовое значение изучаемого признака( отдельные значения случайной величины).

Слайд 4

Основные задачи, которые стоят перед математической статистикой:
1. Определение закона распределения случайной

величины по имеющимся статистическим данным ( по выборке – закон распределения для всей генеральной совокупности).
2. Определение неизвестных параметров распределения ( по выборке оценить параметры генеральной совокупности).
3. Задача проверки правдоподобия выдвигаемых статистических гипотез.

Слайд 5

Схема предварительной обработки экспериментальных данных.
1). Сбор экспериментальных данных.
Чтобы определить закон распределения

случайной величины, нужно провести серию измерений или подсчётов для интересующей нас случайной величины (признака).
В результате получаем статистический ряд – это совокупность числовых данных или выборка объёмом n:
Затем производят упорядочивание членов выборки – эта операция называется ранжирование.
Ранжирование -- это расположение всех имеющихся вариант по возрастанию. Получаем ранжированный статистический ряд.

Слайд 6

Пример:
При измерении частоты пульса у 10 пациентов получены следующие результаты: 90,

110, 65, 80, 90, 60, 70, 80, 70, 80
Ранжированный ряд имеет вид: 60, 65, 70, 70, 80, 80, 80, 90, 90, 110.
Колебания изучаемого признака называются варьирование. В нашем примере варьирование - это изменение частоты пульса.

Слайд 7

Схема предварительной обработки экспериментальных данных.
2).Составление вариационного ряда.
Вариационный ряд (статистическое распределение) --

это двойной ряд чисел в котором каждому значению случайной величины соответствует её частота mi (то есть сколько раз случайная величина принимала данное значение).
Если случайная величина (признак) изменяется дискретно, то составляем дискретный вариационный ряд.

Слайд 8

Для нашего примера вариационный ряд имеет вид:
Очевидно, что , где к

– количество различных значений(к=6).
Графическая характеристика дискретного вариационного ряда - это полигон частот:

Слайд 9

Если признак изменяется непрерывно, то составляется интервальный вариационный ряд:
В первой строке

Слайд 10

Пример.

Слайд 11

Если признак изменяется непрерывно, то составляется интервальный вариационный ряд:
В первой строке

указываются интервалы изменения признака, а во второй – частоты, относящиеся к данным интервалам.
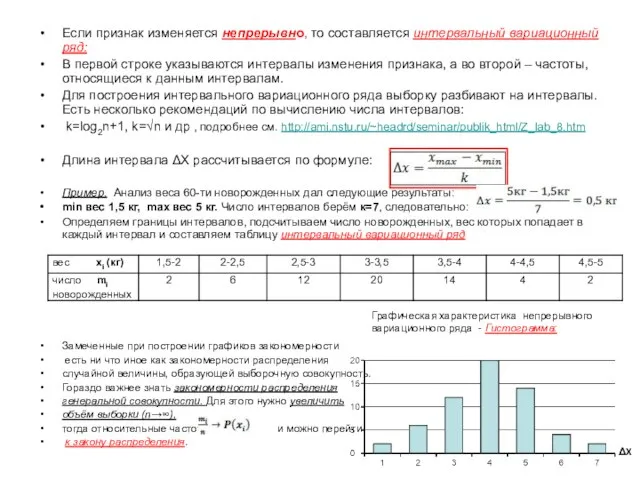
Для построения интервального вариационного ряда выборку разбивают на интервалы. Есть несколько рекомендаций по вычислению числа интервалов:
k=log2n+1, k=√n и др , подробнее см. http://ami.nstu.ru/~headrd/seminar/publik_html/Z_lab_8.htm
Длина интервала ΔX рассчитывается по формуле:
Пример. Анализ веса 60-ти новорожденных дал следующие результаты:
min вес 1,5 кг, max вес 5 кг. Число интервалов берём к=7, следовательно:
Определяем границы интервалов, подсчитываем число новорожденных, вес которых попадает в каждый интервал и составляем таблицу интервальный вариационный ряд
Замеченные при построении графиков закономерности
есть ни что иное как закономерности распределения
случайной величины, образующей выборочную совокупность.
Гораздо важнее знать закономерности распределения
генеральной совокупности. Для этого нужно увеличить
объём выборки (n→∞),
тогда относительные частоты и можно перейти
к закону распределения.

Графическая характеристика непрерывного вариационного ряда - Гистограмма:

ΔX

Слайд 12

2. Статистические характеристики совокупности.
Математическое ожидание M[X],дисперсия D[X],среднее квадратическое отклонение σ[X] --

это числовые характеристики (параметры), которые характеризуют генеральную совокупность.
Если из генеральной совокупности извлечь выборку объёмом n, то она будет иметь свои параметры:
среднее арифметическое,
дисперсия,
стандартное отклонение (среднее квадратическое)
Это выборочные характеристики или статистики. Они являются точечными оценками параметров генеральной совокупности.
Генеральная совокупность (n→∞) Выборка (n- конечно)
-- несмещённая или исправленная
дисперсия.
Число называется число степеней свободы. В генеральной совокупности при n→∞, различие между n и (n-1) не существенно, для выборки же это различие велико.
Так как из одной генеральной совокупности можно извлечь множество выборок, то в каждой выборке будет своё среднее арифметическое, и ни одно из них не будет равно М[X] генеральной совокупности. Следовательно, среднее арифметическое вычислено с ошибкой относительно М[X], так же как и к D[X] -- это статистические ошибки.

Слайд 13

3. Ошибка среднего арифметического.
Извлечём из генеральной совокупности N выборок, тогда

их средние арифметические сами будут являться значениями случайной величины
. Все эти значения имеют отклонения (рассеивание) от истинного значения М[X].
Это отклонение называется ошибка среднего арифметического, она в n раз меньше отклонения каждого xi от для данной выборки объёмом n
показывает насколько близко получаемое по выборке среднее арифметическое значение, приближается к истинному среднему М[X] генеральной совокупности. Чем больше объём выборки n, тем ближе среднее арифметическое к М[X] генеральной совокупности ( т.е., ошибка меньше, чем больше n). Этот вывод получил название Закон больших чисел.

Слайд 14

4. Доверительный интервал и доверительная вероятность.
Истинные значения М[X] и D[X] можно

найти по генеральной совокупности, что практически невозможно. По выборке из этой совокупности мы находим лишь их точечные оценки и , но насколько их значения близки истинным М[X] и D[X]? Например, как велика разность ? может быть как больше, так и меньше М[X]. Поэтому наряду с точечными оценками, применяют интервальные оценки параметров генеральной совокупности по выборке.
То есть мы хотим найти интервал ΔX, такой что: или
Если известна функция распределения, то этот интервал можно найти из соотношения:
зная границы интервала, мы найдём вероятность случайной величины принимать значения из данного интервала. Но нам требуется решить обратную задачу: определить границы интервала, следовательно, для этого надо заранее задать вероятность, с которой мы этот интервал будем определять. Эту вероятность называют доверительной вероятностью РД, а определённый с её помощью интервал -- доверительным интервалом ΔXд.
Доверительным интервалом какого либо параметра, называют такой интервал, о котором можно сказать, что с вероятностью РД он содержит в себе этот параметр.
Доверительную вероятность обычно берут равной РД=0,95, но в особо ответственных случаях принимают РД=0,99 или даже РД=0,999.
С доверительной вероятностью связан уровень значимости α=1-РД.
Уровень значимости α --это вероятность того, что значение исследуемого параметра не попадёт в доверительный интервал.

Слайд 15

Основная масса случайных величин в биологии и медицине распределена по нормальному

закону распределения, следовательно, задав доверительную вероятность можно определить доверительный интервал:
Например, при РД=0,95
Где стандартное отклонение для случайной величины .
Но для малых выборок (n<30) распределение может значительно отличаться от нормального.
В 1908 г английский математик и химик Уильям Госсет под псевдонимом Стьюдент предложил распределение случайной величины для малых выборок.

Слайд 16

5. Распределение Стьюдента.
Нормированная случайная величина вычисляется по формуле:
Плотность вероятности случайной величины:

Где Вn -- параметр , зависит от n.
По мере увеличения объёма выборок n, распределение Стьюдента довольно быстро приближается к нормальному распределению Гаусса и при n˃30 практически не отличается от него.
Практическим следствием этого открытия явилась возможность определять границы доверительного интервала для М[X] с заданной доверительной вероятностью РД:
коэффициент Стьюдента, находим в таблице для заданной РД и известного n.
Таким образом, определив доверительный интервал, можно записать:

Основные понятия математической статистики. (Лекция 3)

Содержание

Основные понятия математической статистики.Математическая статистика – это раздел математики о методах

Генеральная совокупность – это совокупность всех объектов, которые имеют типичную характеристику

Основные задачи, которые стоят перед математической статистикой:1. Определение закона распределения случайной

Схема предварительной обработки экспериментальных данных.1). Сбор экспериментальных данных.Чтобы определить закон распределения

Пример:При измерении частоты пульса у 10 пациентов получены следующие результаты: 90,

Схема предварительной обработки экспериментальных данных.2).Составление вариационного ряда.Вариационный ряд (статистическое распределение) --

Для нашего примера вариационный ряд имеет вид:Очевидно, что , где к

Если признак изменяется непрерывно, то составляется интервальный вариационный ряд:В первой строке

Пример.

Если признак изменяется непрерывно, то составляется интервальный вариационный ряд:В первой строке

2. Статистические характеристики совокупности. Математическое ожидание M[X],дисперсия D[X],среднее квадратическое отклонение σ[X] --

3. Ошибка среднего арифметического. Извлечём из генеральной совокупности N выборок, тогда

4. Доверительный интервал и доверительная вероятность. Истинные значения М[X] и D[X] можно

Основная масса случайных величин в биологии и медицине распределена по нормальному

5. Распределение Стьюдента. Нормированная случайная величина вычисляется по формуле:Плотность вероятности случайной величины:

Похожие презентации

Основные понятия математической статистики.
Математическая статистика – это раздел математики о методах

Основные задачи, которые стоят перед математической статистикой:
1. Определение закона распределения случайной

Схема предварительной обработки экспериментальных данных.
1). Сбор экспериментальных данных.
Чтобы определить закон распределения

Пример:
При измерении частоты пульса у 10 пациентов получены следующие результаты: 90,

Схема предварительной обработки экспериментальных данных.
2).Составление вариационного ряда.
Вариационный ряд (статистическое распределение) --

Для нашего примера вариационный ряд имеет вид:
Очевидно, что , где к

Если признак изменяется непрерывно, то составляется интервальный вариационный ряд:
В первой строке

Если признак изменяется непрерывно, то составляется интервальный вариационный ряд:
В первой строке

2. Статистические характеристики совокупности.
Математическое ожидание M[X],дисперсия D[X],среднее квадратическое отклонение σ[X] --

3. Ошибка среднего арифметического.
Извлечём из генеральной совокупности N выборок, тогда

4. Доверительный интервал и доверительная вероятность.
Истинные значения М[X] и D[X] можно

5. Распределение Стьюдента.
Нормированная случайная величина вычисляется по формуле:
Плотность вероятности случайной величины: