Содержание
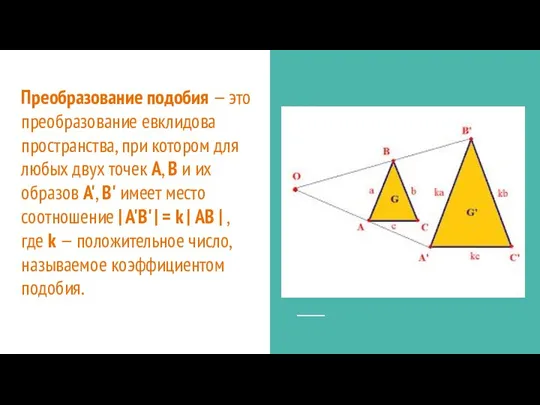
- 2. Преобразование подобия — это преобразование евклидова пространства, при котором для любых двух точек A, B и
- 3. Тела называются подобными, если существует такое преобразование подобия, переводящее одно тело (Ф1) в другое (Ф2).
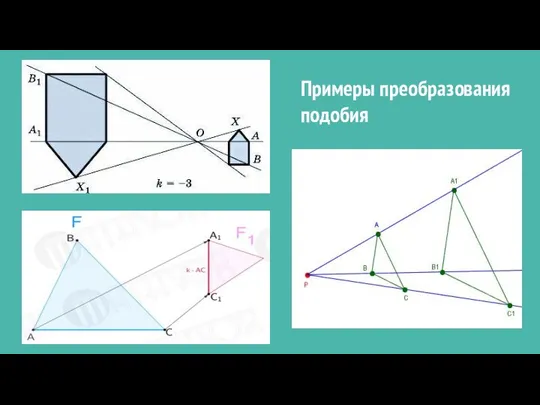
- 4. Примеры преобразования подобия
- 5. На практике подобные фигуры можно получить, например, поместив под лампой вырезанную из куска картона фигуру F,
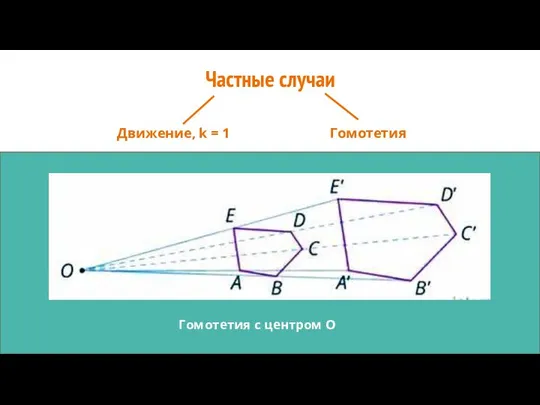
- 6. Частные случаи Движение, k = 1 Гомотетия Гомотетия с центром О
- 7. Теорема о гомотетии Теорема: Гомотетия есть преобразование подобия Доказательство: Пусть О -- центр гомотетии, k --
- 8. При преобразовании подобия углы сохраняют свою величину. Пусть угол ABC преобразованием подобия с коэффициентом k переводится
- 9. Практическое применение
- 11. Скачать презентацию





 Решение задач
Решение задач Ідентифікація параметрів математичної моделі. Основні принципи побудови моделі
Ідентифікація параметрів математичної моделі. Основні принципи побудови моделі Основные формулы тригонометрии
Основные формулы тригонометрии Математическая прогрессия и где её применяют
Математическая прогрессия и где её применяют Свойства тройных интегралов
Свойства тройных интегралов Теорема Пифагора
Теорема Пифагора КАК ЛЮДИ СЧИТАЛИ В СТАРИНУ И КАК ПИСАЛИ ЦИФРЫ Демонстрационный материал к уроку
КАК ЛЮДИ СЧИТАЛИ В СТАРИНУ И КАК ПИСАЛИ ЦИФРЫ Демонстрационный материал к уроку  Основы теории технических измерений
Основы теории технических измерений Векторы плоскости
Векторы плоскости Занимательные задачи Я.И. Перельмана
Занимательные задачи Я.И. Перельмана Аксиома параллельных прямых
Аксиома параллельных прямых Типы случайных событий и действия над ними. Теория вероятностей
Типы случайных событий и действия над ними. Теория вероятностей Центральные и вписанные углы
Центральные и вписанные углы Презентация по математике "Математическая игра Авторалли" - скачать
Презентация по математике "Математическая игра Авторалли" - скачать  Практикум №5 (вторая часть РГР). Построение эконометрических моделей нелинейной парной регрессии (НПР)
Практикум №5 (вторая часть РГР). Построение эконометрических моделей нелинейной парной регрессии (НПР) Натуральный ряд чисел
Натуральный ряд чисел Преобразование выражений, содержащих квадратные корни
Преобразование выражений, содержащих квадратные корни Логические универсальные учебные действия на уроках математики. 7 класс
Логические универсальные учебные действия на уроках математики. 7 класс Описательная статистика
Описательная статистика Алгоритмы вычислительной математики
Алгоритмы вычислительной математики Координатная плоскость
Координатная плоскость Творческий проект по математике. Остров «Матекрип»
Творческий проект по математике. Остров «Матекрип» Задача № 3.028. Решение задачи
Задача № 3.028. Решение задачи Определение синуса и косинуса угла
Определение синуса и косинуса угла Старинные русские меры
Старинные русские меры Десятичная запись дробных чисел. 5 класс, урок 99
Десятичная запись дробных чисел. 5 класс, урок 99 Перша і друга ознаки рівності трикутників
Перша і друга ознаки рівності трикутників Кроссворд «Четырехугольники»
Кроссворд «Четырехугольники»