Содержание
- 2. ПРАВИЛО ЛОПИТАЛЯ Теорема Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их
- 3. То есть если существует неопределенность вида то
- 4. ПРИМЕРЫ Вычислить пределы, используя правило Лопиталя: 1
- 5. Решение:
- 6. 2
- 7. Решение:
- 8. ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИЙ ТЕОРЕМА 1 (достаточное условие возрастания функции)
- 9. Если производная дифференцируемой функции положительна внутри некоторого промежутка Х, то она возрастает на этом промежутке.
- 10. ТЕОРЕМА 2 (достаточное условие убывания функции) Если производная дифференцируемой функции отрицательна внутри некоторого промежутка Х, то
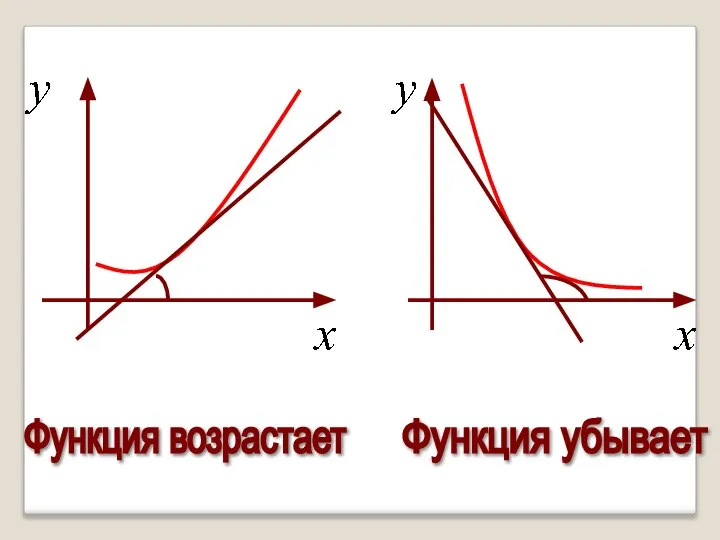
- 11. Геометрическая интерпретация Если касательные к кривой на некотором промежутке направлены под острыми углами к оси х,
- 12. Функция возрастает Функция убывает
- 13. Пример Найти интервалы монотонности функции
- 14. Решение: Найдем производную этой функции: Исследуем знак этой производной:
- 15. Следовательно, функция будет возрастать на промежутке Функция будет убывать на промежутке
- 16. ЭКСТРЕМУМ ФУНКЦИИ Точка х0 называется точкой максимума функции f(x), если в некоторой окрестности точки х0 выполняется
- 17. Точка х1 называется точкой минимума функции f(x), если в некоторой окрестности точки х1 выполняется неравенство
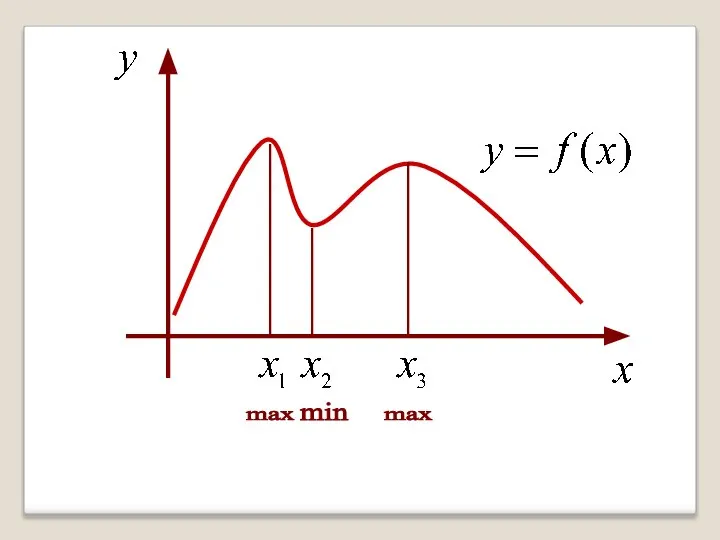
- 18. Значения функции в точках х0 и х1 называются соответственно точками максимума и минимума. Максимум и минимум
- 19. max min max
- 20. Если в некоторой точке х0 дифференцируемая функция f(x) имеет экстремум, то в некоторой окрестности этой точки
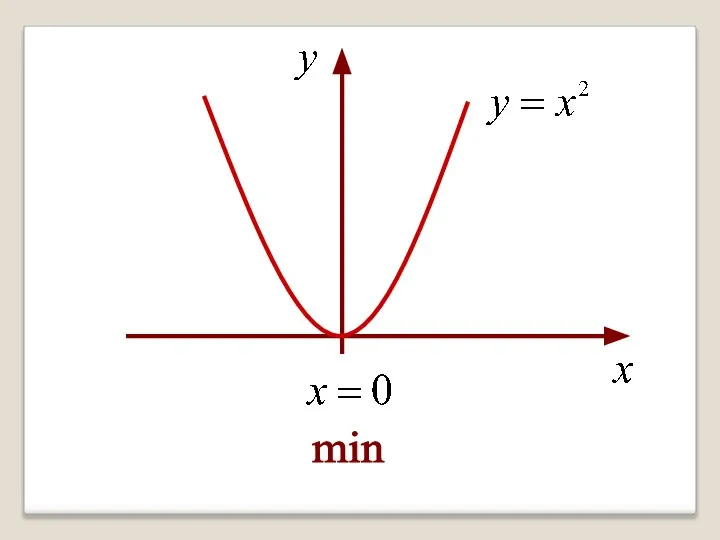
- 21. Однако, функция может иметь экстремум в точке, в которой она не дифференцируема. Например, функция имеет минимум
- 22. Необходимое условие экстремума Для того, чтобы функция y=f(x) имела экстремум в точке х0 , необходимо, чтобы
- 23. Точки, в которых выполняется необходимое условие экстремума, называются критическими или стационарными. Если в какой-либо точке имеется
- 24. Примеры Найти критические точки и экстремумы функций: 1
- 25. Решение: Применим необходимое условие экстремума: - критическая точка
- 26. min
- 27. 2
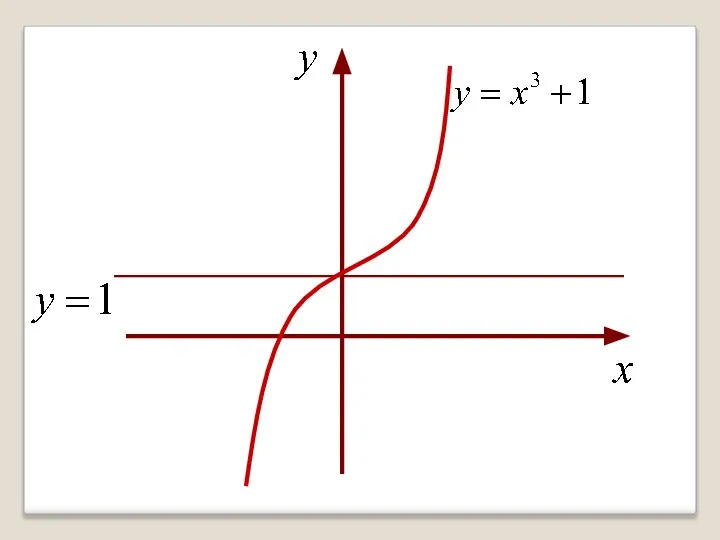
- 28. Решение: Применим необходимое условие экстремума: - критическая точка
- 30. Первое достаточное условие экстремума Если при переходе через точку х0 производная дифференцируемой функции y=f(x) меняет знак
- 31. Схема исследования функции на экстремум 1 Найти производную функции
- 32. 2 Найти критические точки функции, в которых производная равна нулю или не существует.
- 33. 3 Исследовать знак производной слева и справа от каждой критической точки.
- 34. 4 Найти экстремум функции.
- 35. Пример Исследовать функцию на экстремум:
- 36. Решение: Применим схему исследования функции на экстремум: 1 Находим производную функции:
- 37. 2 Находим критические точки: критические точки
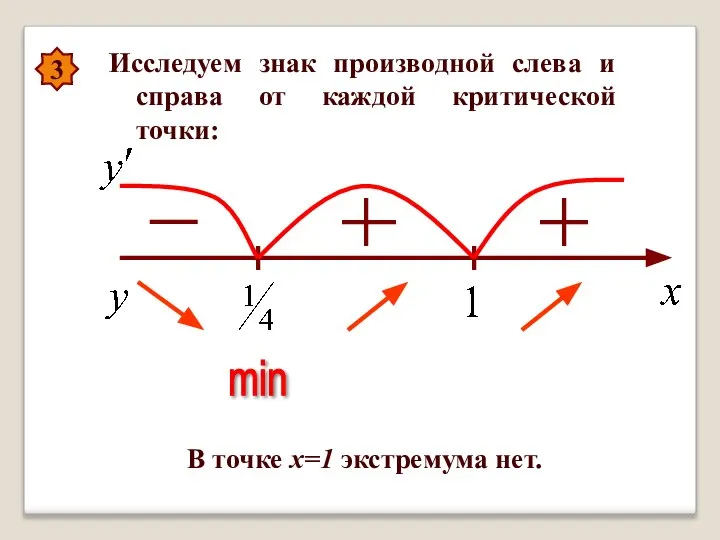
- 38. 3 Исследуем знак производной слева и справа от каждой критической точки: min В точке х=1 экстремума
- 39. 4 Находим экстремум функции:
- 40. Второе достаточное условие экстремума Если первая производная дифференцируемой функции y=f(x) в точке х0 равна нулю, а
- 41. Схема исследования функции на экстремум в этом случае аналогична предыдущей, но третий пункт следует заменить на:
- 42. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ Согласно теореме Вейерштрасса, если функция непрерывна на отрезке [a;b],
- 43. Схема нахождения наибольшего и наименьшего значения функции на отрезке 1 Найти производную функции.
- 44. 2 Найти критические точки, в которых производная равна нулю или не существует. 3 Найти значения функции
- 45. пример Найти наибольшее и наименьшее значения функции на отрезке
- 46. решение: 1 Находим производную функции: 2 Находим критические точки: критические точки
- 47. 3 Находим значения функций в критических точках и на концах отрезка:
- 49. Скачать презентацию









































 Квадратный трехчлен и его корни
Квадратный трехчлен и его корни Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Признаки параллельности двух прямых
Признаки параллельности двух прямых Презентация на тему Галерея великих математиков
Презентация на тему Галерея великих математиков  Начертательная геометрия. Пересечение плоскостей
Начертательная геометрия. Пересечение плоскостей Центр начального образования. Формирование и мониторинг умений младших школьников по разделу «Работа с текстовой задачей»
Центр начального образования. Формирование и мониторинг умений младших школьников по разделу «Работа с текстовой задачей» Осевая и центральная симметрии
Осевая и центральная симметрии Математика 2 класс Урок разработан учителем начальных классов МОУ «СОШ №48» Крыцыной Еленой Анатольевной
Математика 2 класс Урок разработан учителем начальных классов МОУ «СОШ №48» Крыцыной Еленой Анатольевной Деление и умножение десятичных дробей на натуральные числа
Деление и умножение десятичных дробей на натуральные числа Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю Решение уравнений. Решение задач прикладного содержания
Решение уравнений. Решение задач прикладного содержания Тест. Толерантность + Математика
Тест. Толерантность + Математика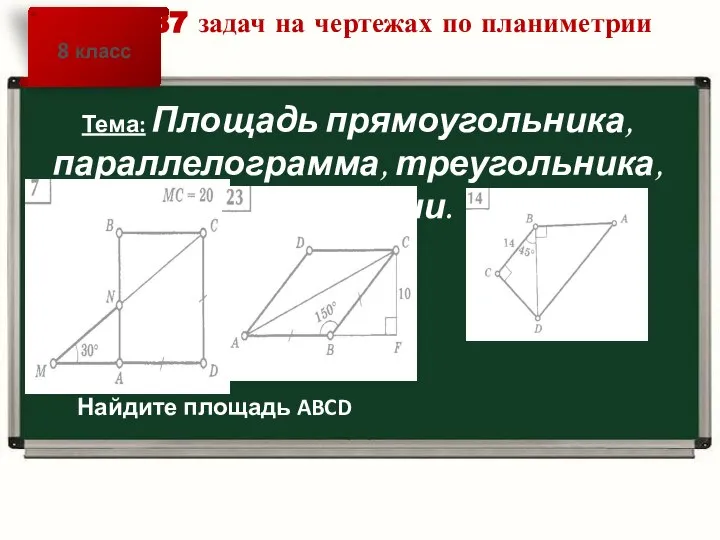 Найдите площадь ABCD
Найдите площадь ABCD Действия с десятичными дробями
Действия с десятичными дробями Как нарисовать многоконечную звезду
Как нарисовать многоконечную звезду Сложение и вычитание обыкновенных дробей
Сложение и вычитание обыкновенных дробей Тренировочный тест. Значение выражений
Тренировочный тест. Значение выражений Арифметик прогрессия. 9 класс
Арифметик прогрессия. 9 класс Постороение графиков функций
Постороение графиков функций Первые действия с числами Лоретц Анна Васильевна, учитель начальных классов, МОУ «СОШ №17», г. Краснотурьинск, Свердловска
Первые действия с числами Лоретц Анна Васильевна, учитель начальных классов, МОУ «СОШ №17», г. Краснотурьинск, Свердловска Презентация по математике "системы счисления" - скачать бесплатно
Презентация по математике "системы счисления" - скачать бесплатно Интерактивный тренажёр Реши уравнения
Интерактивный тренажёр Реши уравнения Сравнение десятичных дробей
Сравнение десятичных дробей Симетрія
Симетрія Прямоугольный треугольник
Прямоугольный треугольник Открытый урок по математике в 3 классе. Тема: умножение вида 50 умножить на 9, 200 умножить на 4. 5 февраля 2013 год. Учитель:Дукова Г.Н.
Открытый урок по математике в 3 классе. Тема: умножение вида 50 умножить на 9, 200 умножить на 4. 5 февраля 2013 год. Учитель:Дукова Г.Н.  Урок в 5 классе Составила учитель математики и информатики, I дидактическая степень, Арнаут Алла Л. АТО, Гагаузия, Комратский район
Урок в 5 классе Составила учитель математики и информатики, I дидактическая степень, Арнаут Алла Л. АТО, Гагаузия, Комратский район Тема урока: «Решение комбинаторных задач с помощью графов»
Тема урока: «Решение комбинаторных задач с помощью графов»