Содержание
- 2. Теорема Вейерштрасса Нахождение наибольшего и наименьшего значений непрерывной функции y=f(x) на отрезке [a;b]. Теорема (1) Непрерывная
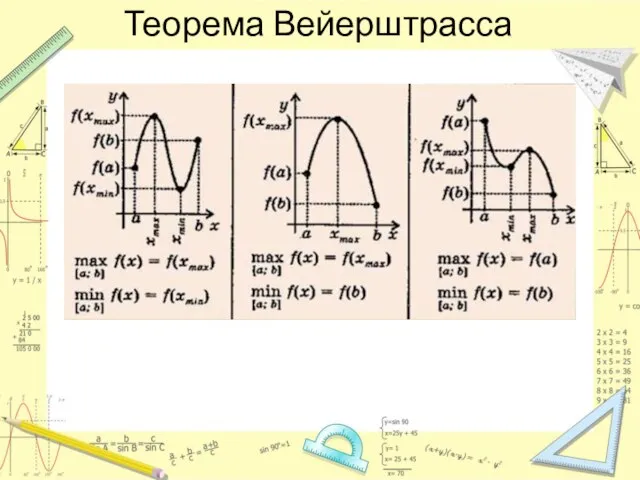
- 3. Теорема Вейерштрасса
- 4. Теорема Вейерштрасса Алгоритм 1. Найти критические точки функции y=f(x). 2. Выбрать из них те, которые принадлежат
- 5. Теорема Вейерштрасса Задача 1. Найти наибольшее и наименьшее значения функции y=f(x) на [a;b]: а) Решение:
- 6. Теорема Вейерштрасса Задача 1. Найти наибольшее и наименьшее значения функции y=f(x) на [a;b]: б) Решение:
- 7. Теорема Вейерштрасса Задача 1. Найти наибольшее и наименьшее значения функции y=f(x) на [a;b]: в) Решение:
- 8. Теорема Вейерштрасса Задача 1. Найти наибольшее и наименьшее значения функции y=f(x) на [a;b]: г) Решение: При
- 9. Теорема Вейерштрасса А как действовать, если необходимо найти наименьшее и наибольшее значения не на отрезке [a;b],
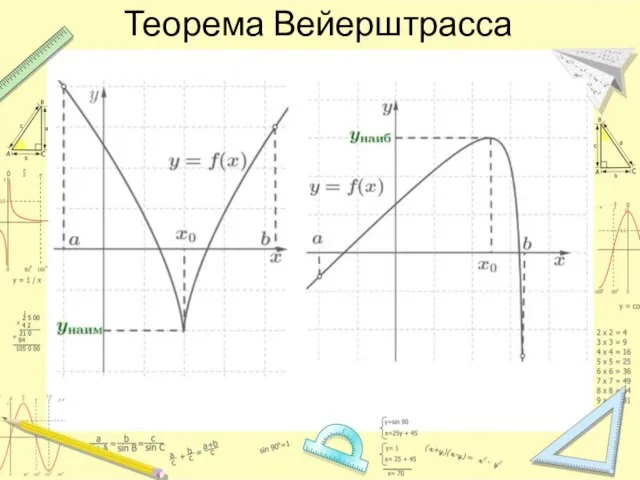
- 10. Теорема Вейерштрасса
- 11. Экстремальные задачи Экстремальные задачи – это задачи на поиск оптимального (наилучшего, самого выгодного, наибольшего и т.п.)
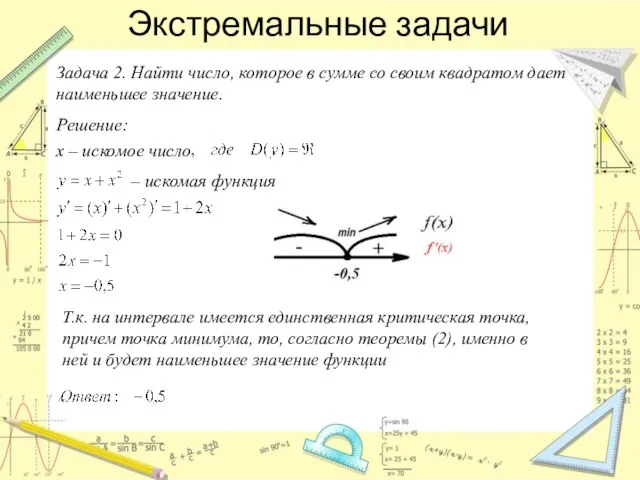
- 12. Экстремальные задачи Задача 2. Найти число, которое в сумме со своим квадратом дает наименьшее значение. Решение:
- 13. Экстремальные задачи Задача 3. Имеется бревно цилиндрической формы диаметром 30см. Из него требуется изготовить брус прямоугольного
- 15. Скачать презентацию


![Теорема Вейерштрасса Задача 1. Найти наибольшее и наименьшее значения функции y=f(x) на [a;b]: а) Решение:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/613245/slide-4.jpg)
![Теорема Вейерштрасса Задача 1. Найти наибольшее и наименьшее значения функции y=f(x) на [a;b]: б) Решение:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/613245/slide-5.jpg)
![Теорема Вейерштрасса Задача 1. Найти наибольшее и наименьшее значения функции y=f(x) на [a;b]: в) Решение:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/613245/slide-6.jpg)




 Статистические оценки параметров распределения случайных величин по выборкам. Вариационные ряды и их графики
Статистические оценки параметров распределения случайных величин по выборкам. Вариационные ряды и их графики Викторина «О, счастливчик» (шуточные тесты математика вокруг нас) Подготовила Учитель математики СОШ№11 Лапшова Татьяна Григорье
Викторина «О, счастливчик» (шуточные тесты математика вокруг нас) Подготовила Учитель математики СОШ№11 Лапшова Татьяна Григорье Рациональные неравенства. Задания для устного счета
Рациональные неравенства. Задания для устного счета Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3
Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3 Символика и терминология. Системы координат. Лекция 1
Символика и терминология. Системы координат. Лекция 1 Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Тема урока: Применение различных способов разложения на множители многочлена Презентацию выполнила Шурыгина И.В.
Тема урока: Применение различных способов разложения на множители многочлена Презентацию выполнила Шурыгина И.В.  Теорема о точке пересечения высот треугольника
Теорема о точке пересечения высот треугольника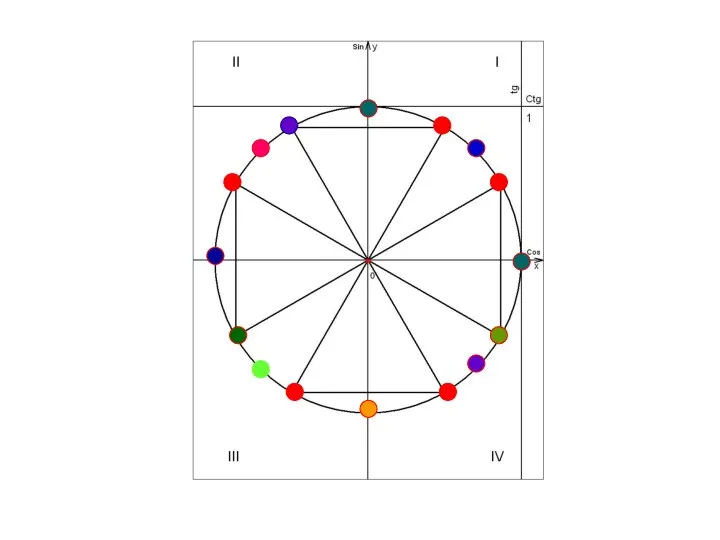 Числовая окружность
Числовая окружность Математика 2 класс. Часть 1
Математика 2 класс. Часть 1 Сочетательное и распределительное свойства умножения
Сочетательное и распределительное свойства умножения Кадры, производительность труда, заработная плата
Кадры, производительность труда, заработная плата Логическая равносильность формул
Логическая равносильность формул Decision trees. Деревья решений
Decision trees. Деревья решений Проверка умножения
Проверка умножения Урок математики
Урок математики Тригонометрические формулы
Тригонометрические формулы Статистические параметры выборки. Закономерности случайной вариации. Оценка достоверности статистических параметров
Статистические параметры выборки. Закономерности случайной вариации. Оценка достоверности статистических параметров Обобщающий урок по теме «Соотношения между сторонами и углами треугольника»
Обобщающий урок по теме «Соотношения между сторонами и углами треугольника» Правило Лопиталя
Правило Лопиталя Алгебра логики. (Лекция 3)
Алгебра логики. (Лекция 3) Куб. Свойства куба
Куб. Свойства куба Натуральные числа. Сравниваем, округляем, отмечаем на координатном луче, решаем комбинаторные задачи
Натуральные числа. Сравниваем, округляем, отмечаем на координатном луче, решаем комбинаторные задачи Уравнение Х2=a
Уравнение Х2=a Кружковое занятие. Тема: Решение задач с помощью проведения прямой, параллельной одной из сторон данного треугольника
Кружковое занятие. Тема: Решение задач с помощью проведения прямой, параллельной одной из сторон данного треугольника Свойства логарифмов
Свойства логарифмов Четырехугольники
Четырехугольники Числовые ряды. Признаки сходимости числовых рядов. Лекция 12
Числовые ряды. Признаки сходимости числовых рядов. Лекция 12