Содержание
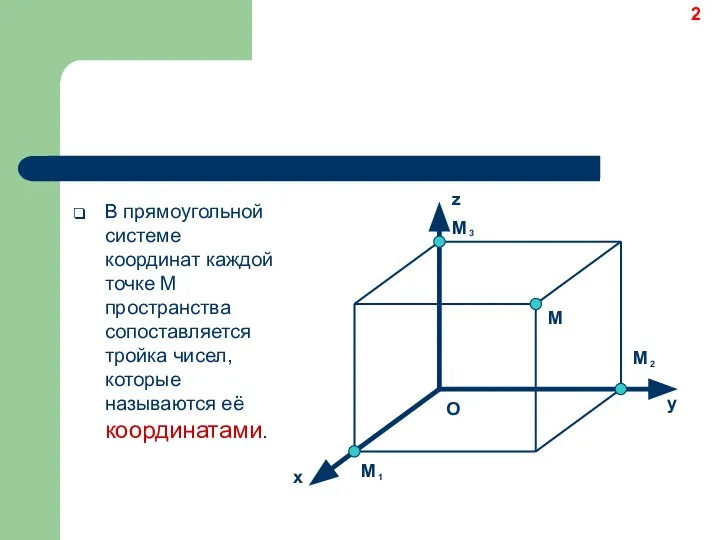
- 2. В прямоугольной системе координат каждой точке M пространства сопоставляется тройка чисел, которые называются её координатами. y
- 3. Разложение по координатным векторам Любой вектор a можно разложить по координатным векторам, т.е. представить в виде
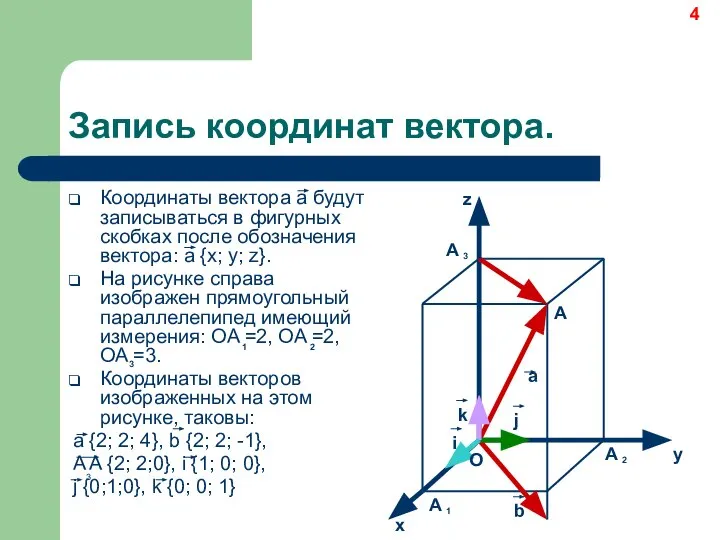
- 4. Запись координат вектора. Координаты вектора а будут записываться в фигурных скобках после обозначения вектора: а {x;
- 5. Нулевой вектор и равные вектора Так как нулевой вектор можно представить в виде 0 = 0i
- 6. Правила нахождения суммы, разности и произведения на данное число. Каждая координата суммы двух или более векторов
- 7. Правило №2 Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Если a {x
- 8. Правило №3 Каждая координата произведения вектора на число равна произведение соответствующей координаты вектора на это число.
- 9. Связь между координатами векторов и координатами точек. Вектор, конец которого совпадает с данной точкой, а начало
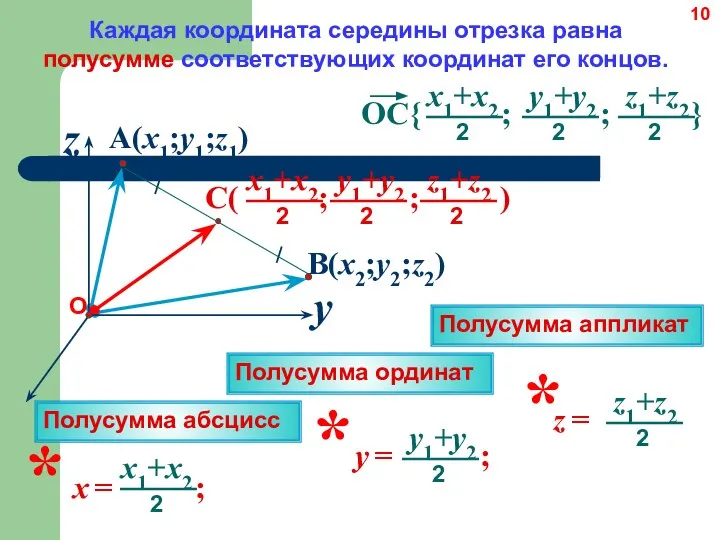
- 10. A(x1;y1;z1) z y B(x2;y2;z2) Каждая координата середины отрезка равна полусумме соответствующих координат его концов. Полусумма абсцисс
- 11. Простейшие задачи в координатах Каждая координата середины отрезка равна полусумме соответствующих координат его концов. Длина вектора
- 13. Скачать презентацию







 Признаки равенства треугольников
Признаки равенства треугольников Сумма углов треугольника
Сумма углов треугольника Презентация по математике "Преобразования фигур. Движение. Векторы, действия с векторами" - скачать бесплатно
Презентация по математике "Преобразования фигур. Движение. Векторы, действия с векторами" - скачать бесплатно Обратные тригонометрические функции
Обратные тригонометрические функции Дискретные случайные величины
Дискретные случайные величины Путешествие с Фалесом по Египту и Греции
Путешествие с Фалесом по Египту и Греции Расширение множества натуральных чмсел
Расширение множества натуральных чмсел Оптимальное планирование эксперимента
Оптимальное планирование эксперимента Сложение дробей, 5 класс (задачи)
Сложение дробей, 5 класс (задачи) Проценты в жизни человека
Проценты в жизни человека Задачи на проценты
Задачи на проценты Применение мультимедийных презентаций для изучения геометрического материала на уроках математики в 5-6 классах. Модуль 3
Применение мультимедийных презентаций для изучения геометрического материала на уроках математики в 5-6 классах. Модуль 3 Аксиомы стереометрии и их следствия
Аксиомы стереометрии и их следствия Упрощение выражений
Упрощение выражений Презентация на тему Звездный математический час
Презентация на тему Звездный математический час  Algorithms for solving NP problems
Algorithms for solving NP problems Суждение как логическая форма. Молекулярное, сложное суждение. (Лекция 4)
Суждение как логическая форма. Молекулярное, сложное суждение. (Лекция 4) Метрология. Основные понятия
Метрология. Основные понятия Домики для гномиков. Счёт в пределах 10. Дидактическая игра по математике
Домики для гномиков. Счёт в пределах 10. Дидактическая игра по математике Решение практико-ориентированных задач
Решение практико-ориентированных задач Теорема Пифагора. Шаржи
Теорема Пифагора. Шаржи Вероятность равновозможных событий
Вероятность равновозможных событий Исторические задачи
Исторические задачи Презентация по математике "Четырехугольники. Свойства четырехугольников. Решение задач" - скачать
Презентация по математике "Четырехугольники. Свойства четырехугольников. Решение задач" - скачать  Направления и наклоны. Введение. (Модуль 1)
Направления и наклоны. Введение. (Модуль 1) Расстояние между двумя точками. Середина отрезка. Координаты середины отрезка. Тема 4
Расстояние между двумя точками. Середина отрезка. Координаты середины отрезка. Тема 4 Решение задач с десятичными дробями
Решение задач с десятичными дробями Неопределенный интеграл. Основные понятия и определения
Неопределенный интеграл. Основные понятия и определения