Содержание
- 2. Методы решения: 1)Матричный метод решения. 2)Метод Крамера. 3) Метод Гаусса
- 3. 1)Матричный метод решения. Запишем заданную систему в матричном виде: АХ=В, где А – основная матрица коэффициентов
- 4. 1)Матричный метод решения. Поэтому, чтобы найти неизвестную матрицу Х надо найти обратную матрицу к матрице системы
- 5. Пример 1. Решить систему матричным способом. Решение: Решим систему линейных уравнений матричным методом. Обозначим Тогда данную
- 6. Т.к. матрица невырожденная (Δ= – 2), то X = A-1B.
- 10. Тогда A-1 = Получим X = A-1B = Ответ: х1 = –1, х2 = 4, х3
- 11. 2)Метод Крамера. Метод Крамера (теорема Крамера) — способ решения квадратных СЛАУ с ненулевым определителем основной матрицы.
- 12. где вместо -го столбца стоит столбец правых частей. Пример 2. Решить систему по формулам Крамера. Решение:
- 13. D 0, значит, система имеет единственное решение.
- 15. Ответ: x1 = 5, x2 = -1, x3 = 1.
- 16. 3) Метод Гаусса Метод Гаусса - Метод последовательного исключения неизвестных. Метод Гаусса включает в себя прямой
- 17. Пример 3. Исследовать систему и решить ее методом Гаусса, если она совместна Решение: Дана неоднородная линейная
- 19. (привели матрицу (A,B) к матрице ( ), имеющую ступенчатую форму). Итак, Rg(A, B) = Rg( )
- 21. ⇒ решение найдено верно.
- 23. Скачать презентацию






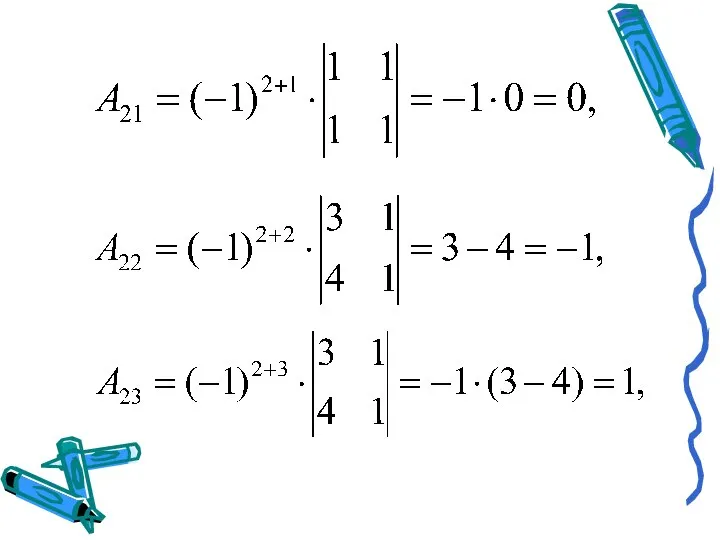
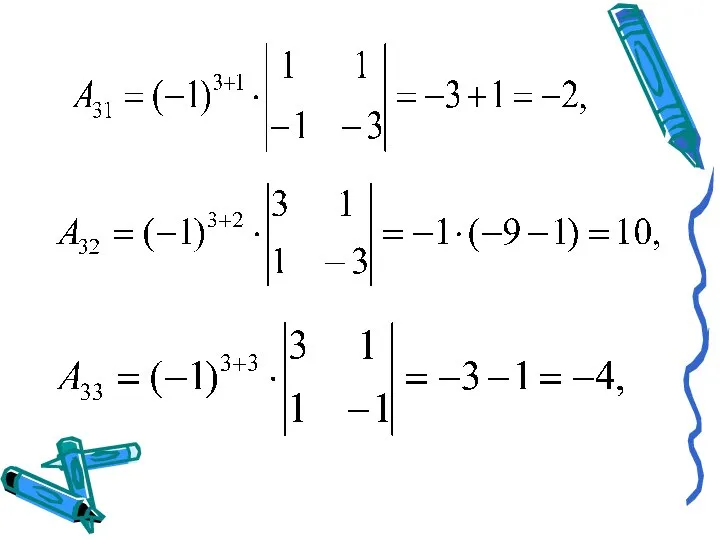




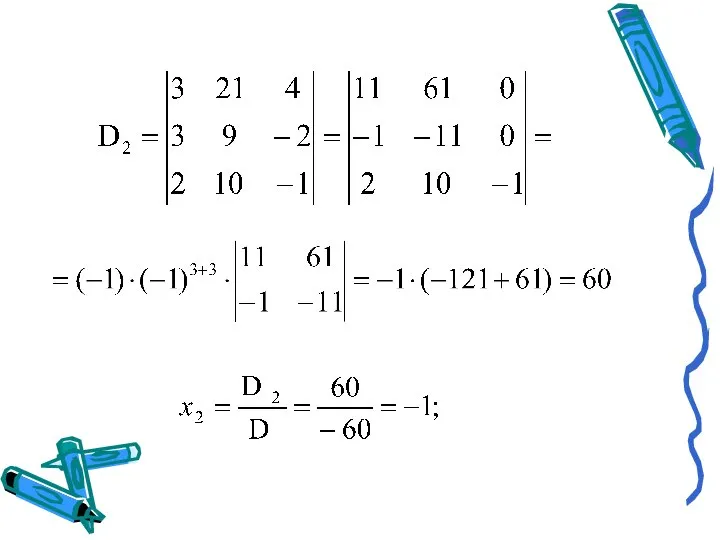
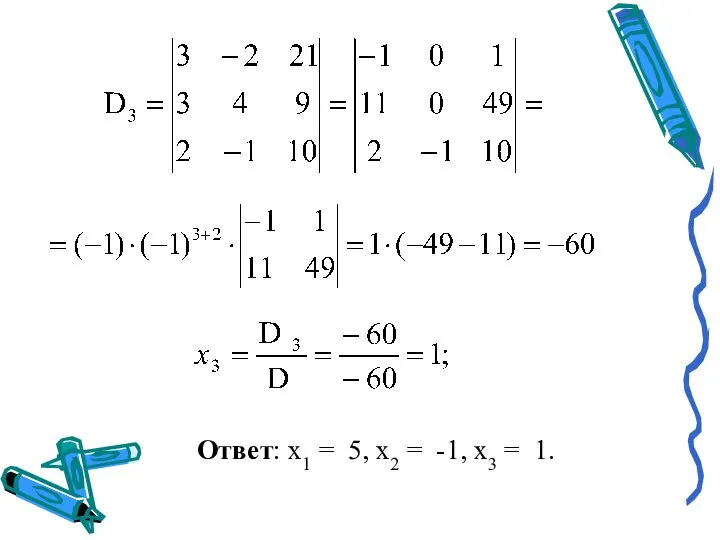






 Преобразования трехмерного пространства
Преобразования трехмерного пространства Определение квадратного уравнения. Неполные квадратные уравнения
Определение квадратного уравнения. Неполные квадратные уравнения Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Единицы измерения, их история
Единицы измерения, их история Параллелограмм и его виды
Параллелограмм и его виды Сумма углов треугольника Решение задач
Сумма углов треугольника Решение задач Імітаційне моделювання
Імітаційне моделювання Уравнение касательной к графику функции
Уравнение касательной к графику функции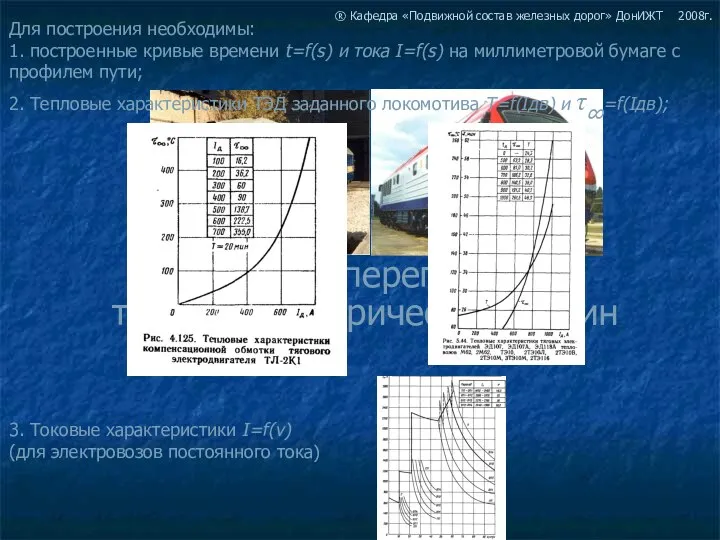 Расчет перегрева тяговых электрических машин
Расчет перегрева тяговых электрических машин Обратная матрица
Обратная матрица Системы уравнений с двумя переменными
Системы уравнений с двумя переменными Решение заданий В8 (часть 1) по материалам открытого банка задач ЕГЭ по математике
Решение заданий В8 (часть 1) по материалам открытого банка задач ЕГЭ по математике Задачи теории расписаний
Задачи теории расписаний Теория вероятности (задачи)
Теория вероятности (задачи) Информационная безопасность. Базовые логические элементы, применяемые в вычислительной технике
Информационная безопасность. Базовые логические элементы, применяемые в вычислительной технике Симметрия вокруг нас
Симметрия вокруг нас Простые числа. Леонард Эйлер
Простые числа. Леонард Эйлер Задачи на движение
Задачи на движение Правильные и неправильные дроби. 5 класс
Правильные и неправильные дроби. 5 класс Объемы. Объем прямоугольного параллелепипеда
Объемы. Объем прямоугольного параллелепипеда Умозаключение по аналогии
Умозаключение по аналогии Решение краевых задач для обыкновенных дифференциальных уравнений второго порядка
Решение краевых задач для обыкновенных дифференциальных уравнений второго порядка Пересечение поверхностей. (Лекция 7)
Пересечение поверхностей. (Лекция 7) Методы непараметрического спектрального анализа. Метод периодограмм
Методы непараметрического спектрального анализа. Метод периодограмм Теорема Пифагора
Теорема Пифагора МОУ «СОШ г. Бирюча» Красногвардейского района Белгородской области Проект на тему: «Великие математики прошлого»
МОУ «СОШ г. Бирюча» Красногвардейского района Белгородской области Проект на тему: «Великие математики прошлого»  Аттестационная работа. Рабочая программа математического кружка Эрудит. (5-6 класс)
Аттестационная работа. Рабочая программа математического кружка Эрудит. (5-6 класс) Задачи по математике
Задачи по математике