Решение заданий С2 (Часть 4 )

Сентябрь 6, 2022

Главная
Математика
Решение заданий С2 (Часть 4 )

Содержание

2. №1 С В D А1 С1 В1 D1 А Решение. Призма прямая, в основании прямоугольник. Значит,
3. №1 φ 90º − φ Решение (продолжение) Информация о том, что эта плоскость проходит через середину
4. №1 С В D А1 С1 В1 D1 А Решение (продолжение) Поскольку мы имеем дело с
5. В Решение. Прямые AA1 и AE перпендикулярны прямой DE. Плоскость DЕА1, содержащая прямую DE, перпендикулярна плоскости
7. Скачать презентацию

Слайд 2

№1
С
В
D
А1
С1
В1
D1
А
Решение.
Призма прямая, в основании прямоугольник. Значит, она еще и прямоугольный

параллелепипед.
Это значит, что расстояние между A1C1 и BD (диагоналями оснований призмы) равно длине боковых ребер .
Нам нужно найти тангенс угла между боковой гранью AA1D1D и плоскостью, перпендикулярной диагонали B1D параллелепипеда.

Слайд 3

№1
φ
90º − φ
Решение (продолжение)
Информация о том, что эта плоскость проходит через

середину ребра CD − лишняя.
Имеем две пересекающиеся плоскости, к одной из которых проведена перпендикулярная прямая B1D, пересекающая другую плоскость в точке D.
По сути, нам надо найти угол между плоскостью грани AA1D1D и самой диагональю B1D − угол φ, а искомый угол будет равен (90º − φ).

В1

Слайд 4

№1
С
В
D
А1
С1
В1
D1
А
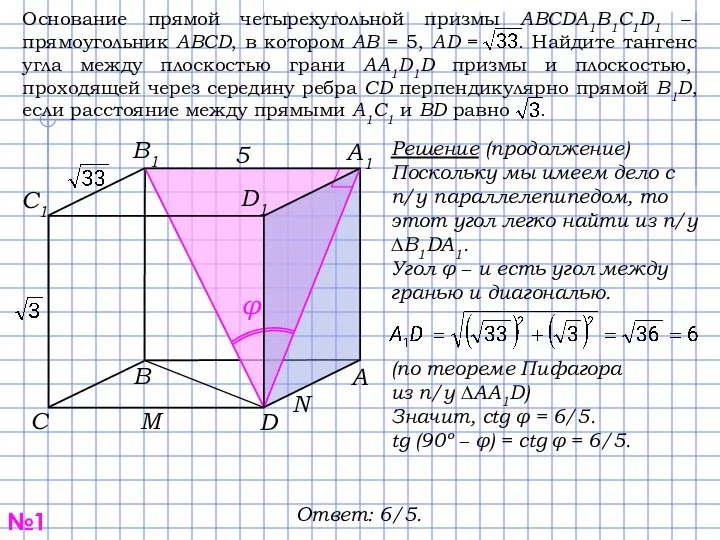
Решение (продолжение)
Поскольку мы имеем дело с п/у параллелепипедом, то этот угол

легко найти из п/у ∆B1DA1.
Угол φ − и есть угол между гранью и диагональю.

(по теореме Пифагора
из п/у ∆AA1D)
Значит, ctg φ = 6/5.
tg (90º − φ) = ctg φ = 6/5.

Ответ: 6/5.

Слайд 5

В
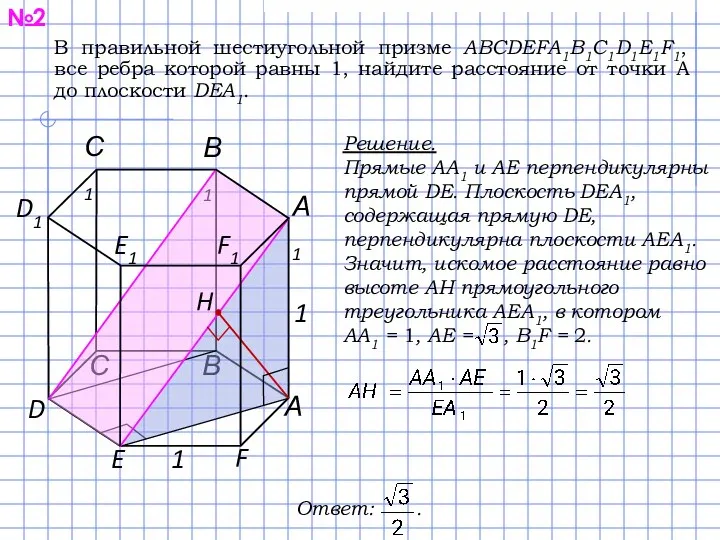
Решение.
Прямые AA1 и AE перпендикулярны прямой DE. Плоскость DЕА1, содержащая

прямую DE, перпендикулярна плоскости AEA1.
Значит, искомое расстояние равно высоте AH прямоугольного треугольника AEA1, в котором
AA1 = 1, AE = , B1F = 2.

В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, найдите расстояние от точки А до плоскости DЕА1.

№2

А1

С1

В1

Решение заданий С2 (Часть 4 )

Содержание

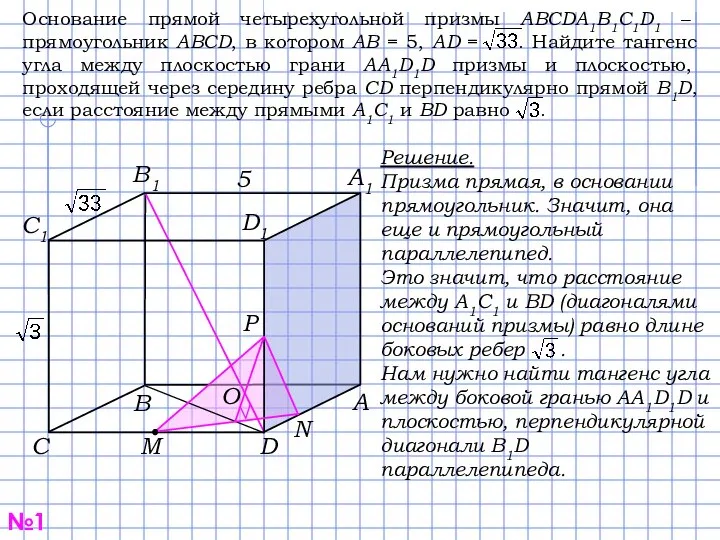
№1СВDА1С1В1D1АРешение. Призма прямая, в основании прямоугольник. Значит, она еще и прямоугольный

№1φ90º − φРешение (продолжение)Информация о том, что эта плоскость проходит через

№1СВDА1С1В1D1АРешение (продолжение)Поскольку мы имеем дело с п/у параллелепипедом, то этот угол

ВРешение. Прямые AA1 и AE перпендикулярны прямой DE. Плоскость DЕА1, содержащая

Похожие презентации

№1
С
В
D
А1
С1
В1
D1
А
Решение.
Призма прямая, в основании прямоугольник. Значит, она еще и прямоугольный

№1
φ
90º − φ
Решение (продолжение)
Информация о том, что эта плоскость проходит через

№1
С
В
D
А1
С1
В1
D1
А
Решение (продолжение)
Поскольку мы имеем дело с п/у параллелепипедом, то этот угол

В
Решение.
Прямые AA1 и AE перпендикулярны прямой DE. Плоскость DЕА1, содержащая