Содержание
- 2. Вычислительные методы решения задач линейного программирования. Сущность симплекс – метода. Примеры решения с использованием симплекс-метода. Учебные
- 3. Вычислительные методы решения задач линейного программирования Учебный вопрос № 1
- 4. Геометрическая интерпретация, при решении задач линейного программирования, перестает быть пригодной для этой цели при числе свободных
- 5. Симплекс-метод — алгоритм решения оптимизационной задачи (ОЗ) линейного программирования путём перебора вершин выпуклого многогранника в многомерном
- 6. Сущность симплекс-метода Учебный вопрос № 2
- 7. Идея симплекс-метода относительно проста. Пусть в задаче линейного программирования имеется n переменных и m независимых линейных
- 8. Предположим, что все свободные переменные х1, х2, …, хk равны нулю. При этом получим: хk+1 =
- 9. Очевидно, что при х1 = х2 = … = хk =0, F = γ0. Проверим, может
- 10. Пусть, например, коэффициент γi в (2) отрицателен. Значит, есть смысл увеличить х1, т. е. перейти от
- 11. Допустим, что это не так и что среди уравнений (1) есть такие, в которых коэффициент при
- 12. Если оставить х2 = х3 = … = хk =0, то х1 можно увеличивать только до
- 13. Первое опорное решение получим, положив равными нулю все прежние свободные переменные х1 , х2 , …
- 14. Предположим, что уравнения типа (1) для нового набора базисных и свободных переменных составлены. Тогда можно выразить
- 15. Примеры решения с использованием симплекс-метода Учебный вопрос № 3
- 16. Пример. Пусть имеется задача линейного программирования с ограничениями-неравенствами: – 5х1 – х2 + 2х3 ≤ 2;
- 17. Приводя неравенства к стандартному виду (≥ 0) и вводя добавочные переменные у1, у2, у3, переходим к
- 18. Пусть в качестве свободных переменных выступают х1, х2, х3, х4. Положим их равными нулю и получим
- 19. Определим, какая из этих переменных (у1 или у2) раньше обратится в нуль при увеличении х3. Очевидно,
- 20. Это выражение подставляется вместо х3 во второе уравнение: (5) Пример (продолжение)
- 21. Что касается третьего уравнения, то оно, как не содержащее х3 не изменится. Система (4) приведена к
- 22. Это решение все еще не оптимально, так как коэффициент при х2 в выражении (6) отрицателен, и
- 23. Выразим F через новые свободные переменные: F = 3х1 + 2у2 – у1 + 2х4 –
- 24. В рассмотренном примере не пришлось искать опорное решение: оно сразу же получилось, когда положили свободные переменные
- 25. ЗАДАНИЕ. Компания производит полки для ванных комнат двух размеров – А и В. Агенты по продаже
- 26. РЕШЕНИЕ. Составим математическую модель задачи. Пусть х1 – количество полок вида А, х2 – количество полок
- 27. Таким образом, приходим к задаче линейного программирования. Решим ее симплекс-методом. Введем три дополнительные переменные x3, x4,
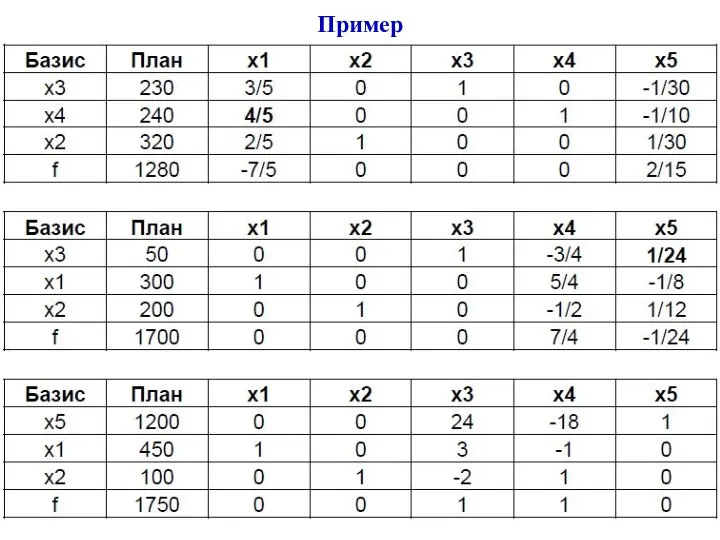
- 28. В качестве опорного плана выберем X0=(0,0,550,1200,9600). Составим симплекс-таблицу. В последней оценочной строке есть отрицательные оценки, поэтому
- 29. Пример
- 30. В последнем плане строка f не содержит отрицательных значений, план x1 = 450, x2 = 100
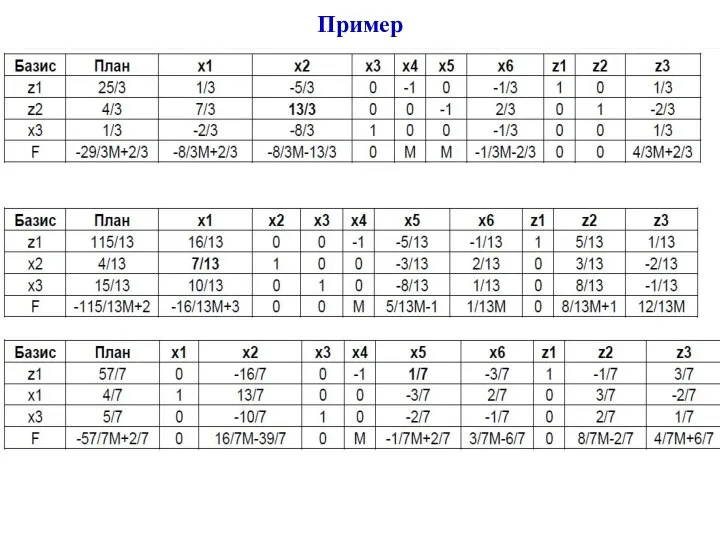
- 31. ЗАДАНИЕ. Решить задачу линейного программирования симплекс-методом. РЕШЕНИЕ. Будем решать эквивалентную задачу Пример
- 32. Введем дополнительные переменные, чтобы привести задачу к каноническому виду: Так как нет единичных векторов, вводим искусственный
- 33. Получили расширенную задачу с опорным планом (0,0,0,0,0,0,8,2,1). Составим cимплекс-таблицу: В последней оценочной строке есть отрицательные оценки
- 34. Пример
- 35. Искусственный базис выведен, но в единственном столбце с отрицательной оценкой (Х2) все коэффициенты отрицательны, то есть
- 37. Скачать презентацию
































 Прямоугольный и треугольные обходы
Прямоугольный и треугольные обходы Перпендикуляр и наклонная к прямой
Перпендикуляр и наклонная к прямой признаки делимости на 10, на 5, на 2
признаки делимости на 10, на 5, на 2 Интеллектуальная игра Математика
Интеллектуальная игра Математика Урок математики в 4 классе по теме: «Порядок действий в сложных выражениях» Выполнила учитель начальных классов высшей квалиф
Урок математики в 4 классе по теме: «Порядок действий в сложных выражениях» Выполнила учитель начальных классов высшей квалиф Предмет и метод статистики
Предмет и метод статистики Прямой угол вокруг нас
Прямой угол вокруг нас Открытый интенсив по математике. Как мощно подготовиться к экзамену? Ценность времени. День 2
Открытый интенсив по математике. Как мощно подготовиться к экзамену? Ценность времени. День 2 Математическое кафе
Математическое кафе Бірмүше және оның стандарт түрі. Бірмүшелерді көбейту және дәрежеге шығару тақырыптарына есептер шығарту
Бірмүше және оның стандарт түрі. Бірмүшелерді көбейту және дәрежеге шығару тақырыптарына есептер шығарту Решение тригонометрических уравнений
Решение тригонометрических уравнений Осевая и центральная симметрии
Осевая и центральная симметрии Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20  Урок математики 6 класс Фролова С. Г., учитель математики МКОУ «Лицей» , г. Калачинск, Омской области
Урок математики 6 класс Фролова С. Г., учитель математики МКОУ «Лицей» , г. Калачинск, Омской области Модели представления задач
Модели представления задач Прибавить и вычесть числа 123. Повторение изученного
Прибавить и вычесть числа 123. Повторение изученного Числа 1, 2, 3. Знаки +, -, =
Числа 1, 2, 3. Знаки +, -, = Практическое применение площадей геометрических фигур
Практическое применение площадей геометрических фигур Площадь криволинейной трапеции
Площадь криволинейной трапеции Планиметрия. Четырёхугольники
Планиметрия. Четырёхугольники Решение задач и выражений. Сравнение именованных чисел
Решение задач и выражений. Сравнение именованных чисел Аттестационная работа. Все профессии важны, с математикой дружны
Аттестационная работа. Все профессии важны, с математикой дружны Векторы в пространстве. (11 класс)
Векторы в пространстве. (11 класс) Измерение углов
Измерение углов Элементы комбинаторики. Примеры комбинаторных задач
Элементы комбинаторики. Примеры комбинаторных задач Математика - 6. Домашнее задание
Математика - 6. Домашнее задание График функции и график уравнения
График функции и график уравнения Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности