Содержание
- 2. Talk outline What is the GJK algorithm Terminology “Simplified” version of the algorithm One object is
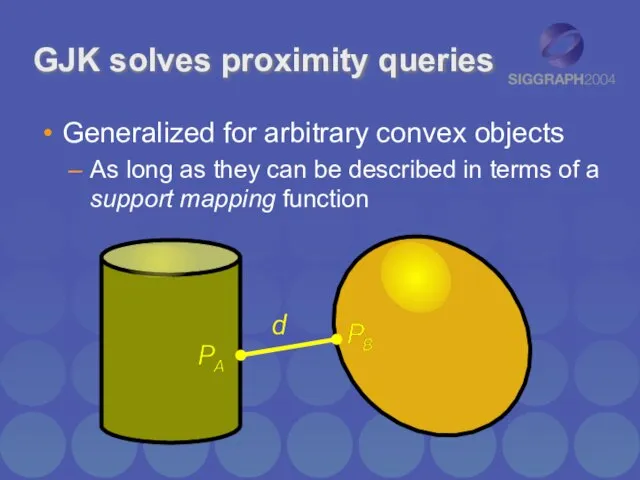
- 3. GJK solves proximity queries Given two convex polyhedra Computes distance d Can also return closest pair
- 4. GJK solves proximity queries Generalized for arbitrary convex objects As long as they can be described
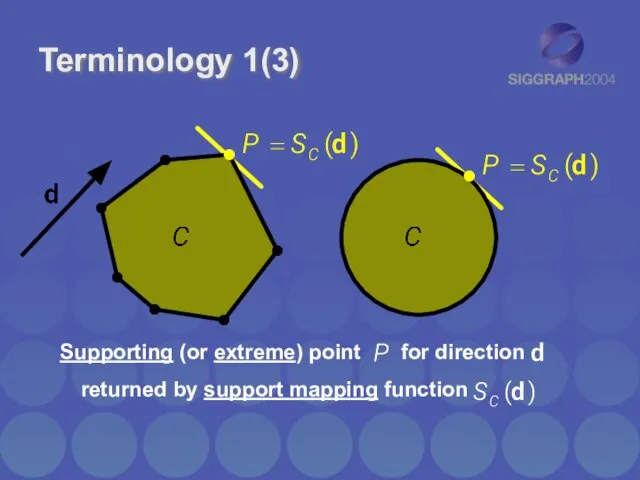
- 5. Terminology 1(3) Supporting (or extreme) point for direction returned by support mapping function
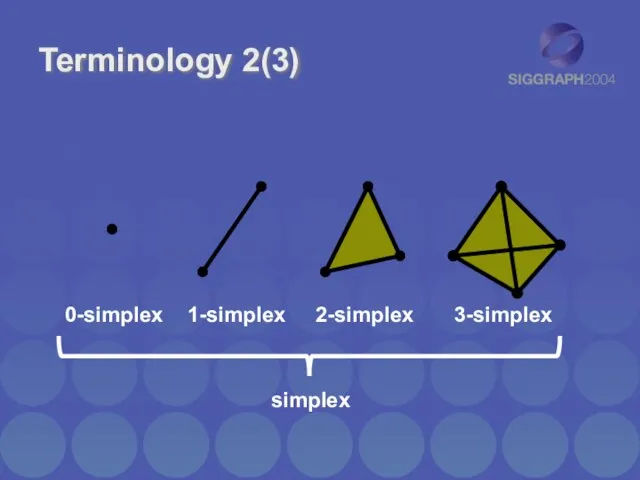
- 6. Terminology 2(3) 0-simplex 1-simplex 2-simplex 3-simplex simplex
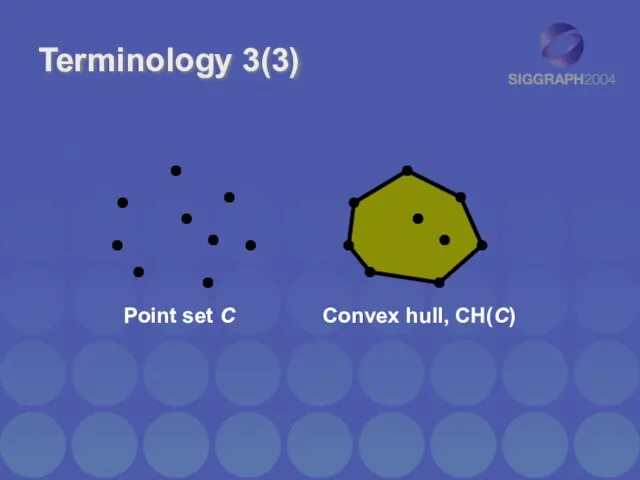
- 7. Terminology 3(3) Point set C Convex hull, CH(C)
- 8. The GJK algorithm Initialize the simplex set Q with up to d+1 points from C (in
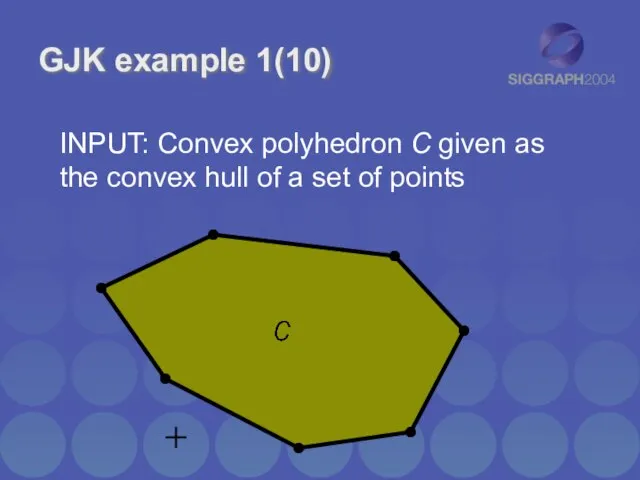
- 9. GJK example 1(10) INPUT: Convex polyhedron C given as the convex hull of a set of
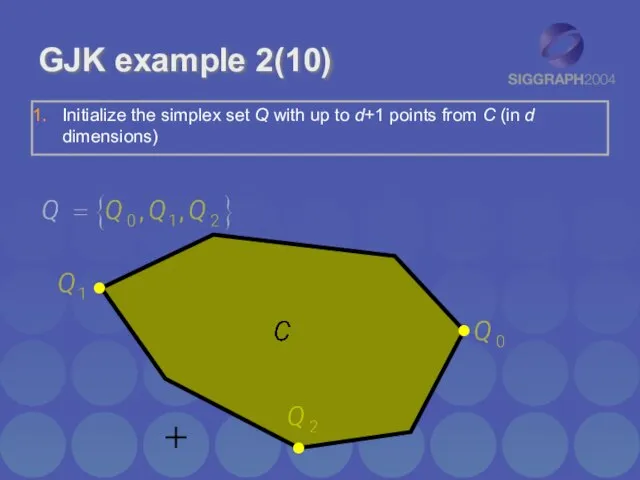
- 10. Initialize the simplex set Q with up to d+1 points from C (in d dimensions) GJK
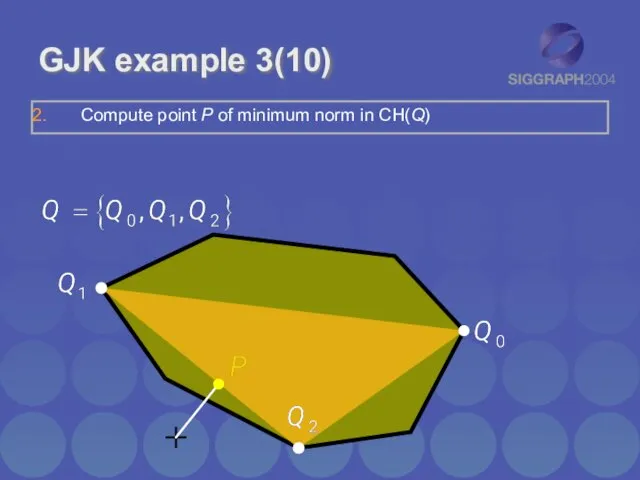
- 11. GJK example 3(10) Compute point P of minimum norm in CH(Q)
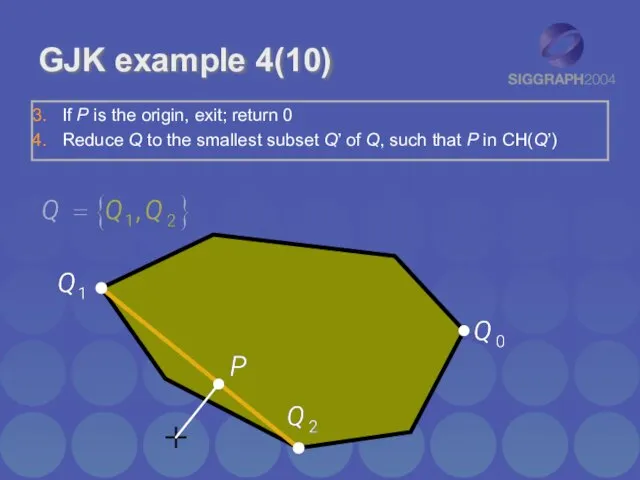
- 12. GJK example 4(10) If P is the origin, exit; return 0 Reduce Q to the smallest
- 13. GJK example 5(10) Let V=SC(–P) be a supporting point in direction –P
- 14. GJK example 6(10) If V no more extreme in direction –P than P itself, exit; return
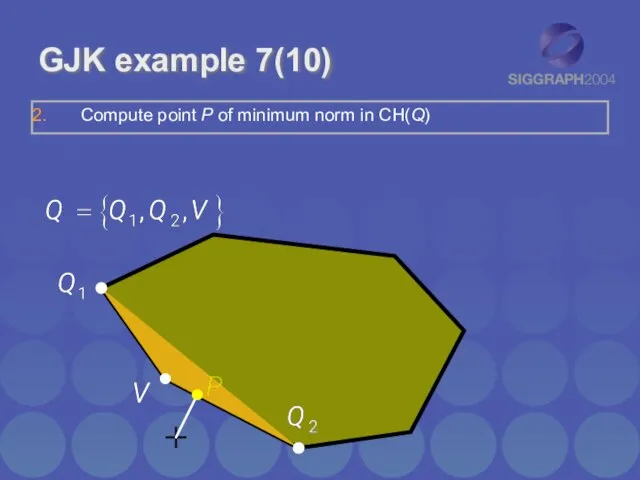
- 15. GJK example 7(10) Compute point P of minimum norm in CH(Q)
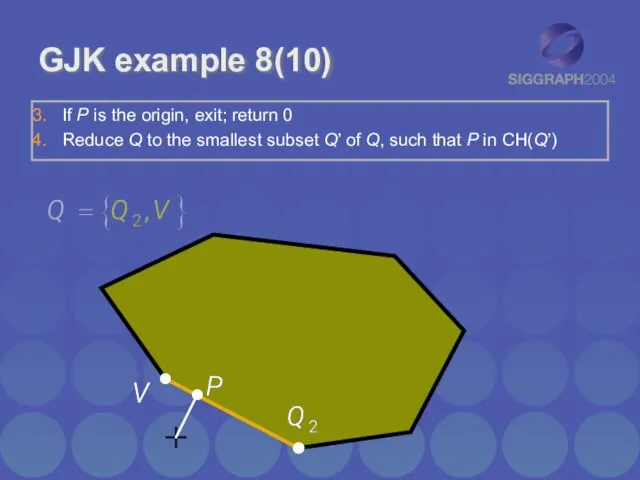
- 16. GJK example 8(10) If P is the origin, exit; return 0 Reduce Q to the smallest
- 17. GJK example 9(10) Let V=SC(–P) be a supporting point in direction –P
- 18. GJK example 10(10) DONE! If V no more extreme in direction –P than P itself, exit;
- 19. Distance subalgorithm 1(2) Approach #1: Solve algebraically Used in original GJK paper Johnson’s distance subalgorithm Searches
- 20. Distance subalgorithm 2(2) Approach #2: Solve geometrically Mathematically equivalent But more intuitive Therefore easier to make
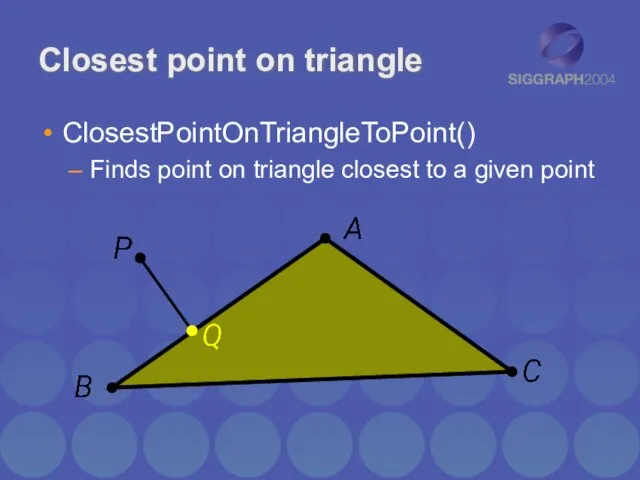
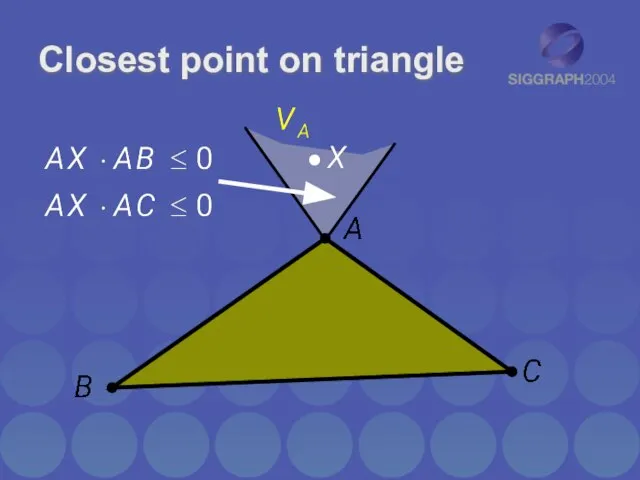
- 21. Closest point on triangle ClosestPointOnTriangleToPoint() Finds point on triangle closest to a given point
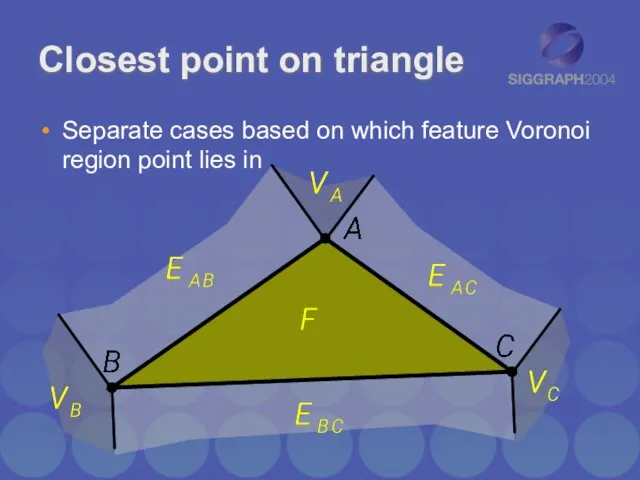
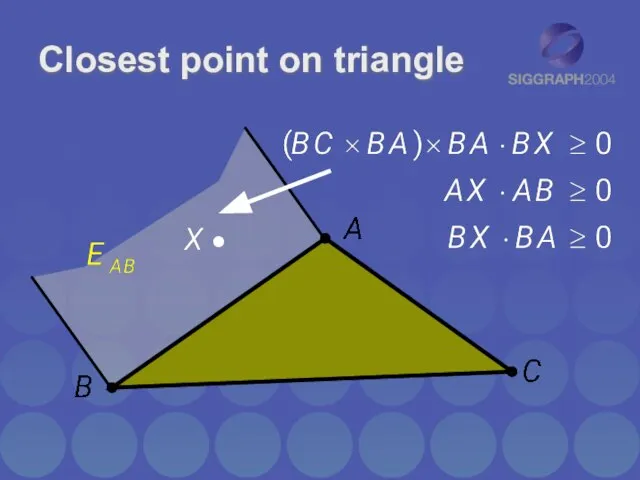
- 22. Closest point on triangle Separate cases based on which feature Voronoi region point lies in
- 23. Closest point on triangle
- 24. Closest point on triangle
- 25. GJK for two objects What about two polyhedra, A and B? Reduce problem into the one
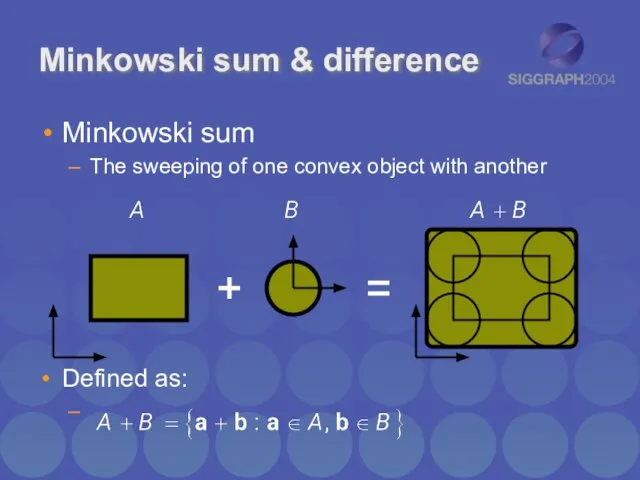
- 26. Minkowski sum & difference Minkowski sum The sweeping of one convex object with another Defined as:
- 27. Minkowski sum & difference Minkowski difference, defined as: Can write distance between two objects as: A
- 28. The generalization A and B intersecting iff A–B contains the origin! Distance between A and B
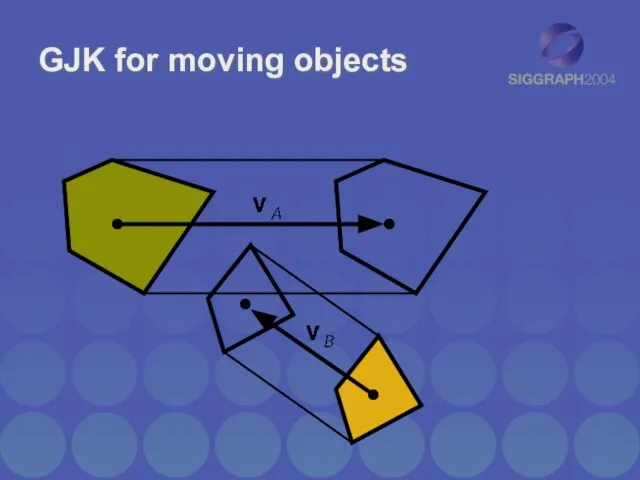
- 29. GJK for moving objects
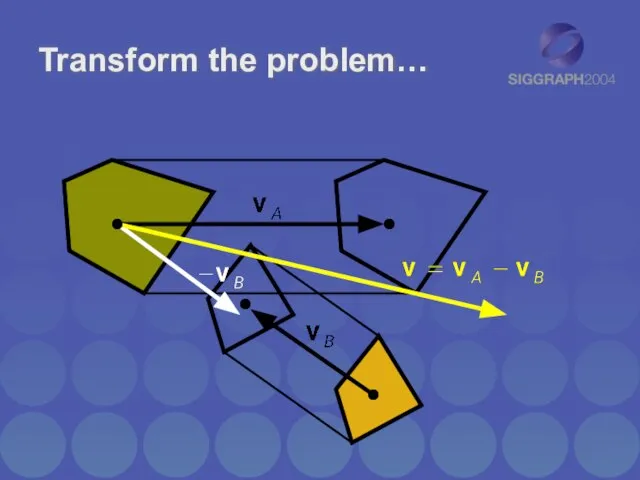
- 30. Transform the problem…
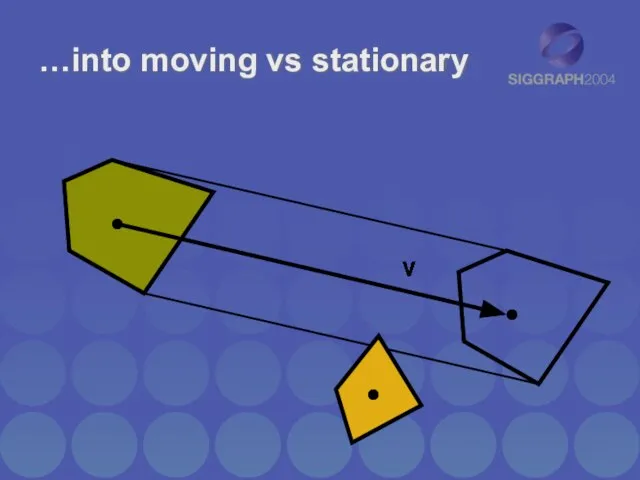
- 31. …into moving vs stationary
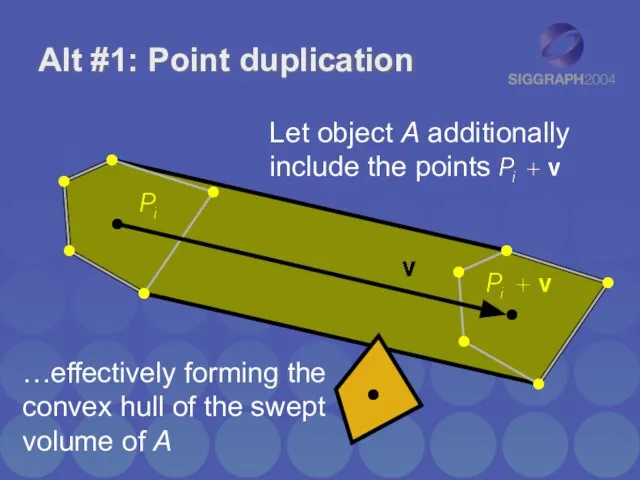
- 32. Alt #1: Point duplication Let object A additionally include the points …effectively forming the convex hull
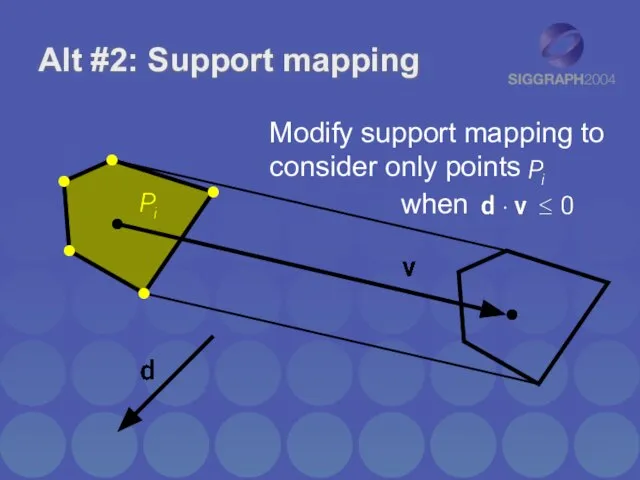
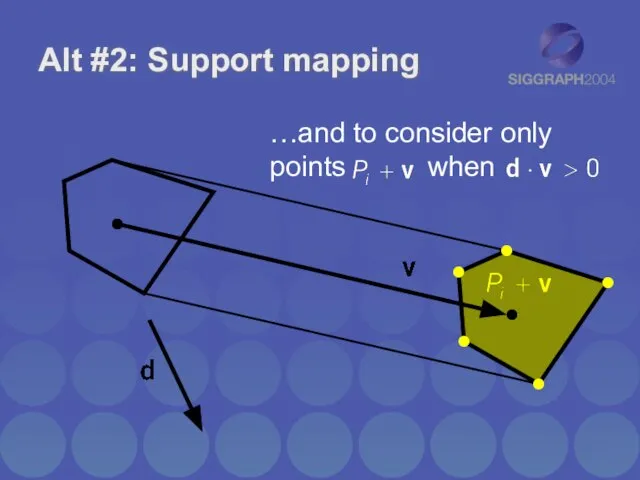
- 33. Alt #2: Support mapping Modify support mapping to consider only points when
- 34. Alt #2: Support mapping …and to consider only points when
- 35. GJK for moving objects Presented solution Gives only Boolean interference detection result Interval halving over v
- 37. Скачать презентацию













 Математическое описание ЭЭС при исследовании электромеханических переходных процессов
Математическое описание ЭЭС при исследовании электромеханических переходных процессов Функция y=sin x, её свойства и график
Функция y=sin x, её свойства и график Презентация на тему Выполните задание дроби
Презентация на тему Выполните задание дроби Презентация по математике "Математические ребусы" - скачать бесплатно
Презентация по математике "Математические ребусы" - скачать бесплатно Пирамида. Усеченная пирамида
Пирамида. Усеченная пирамида Анаграмма. Великолепная семерка
Анаграмма. Великолепная семерка Сложение и вычитание векторов
Сложение и вычитание векторов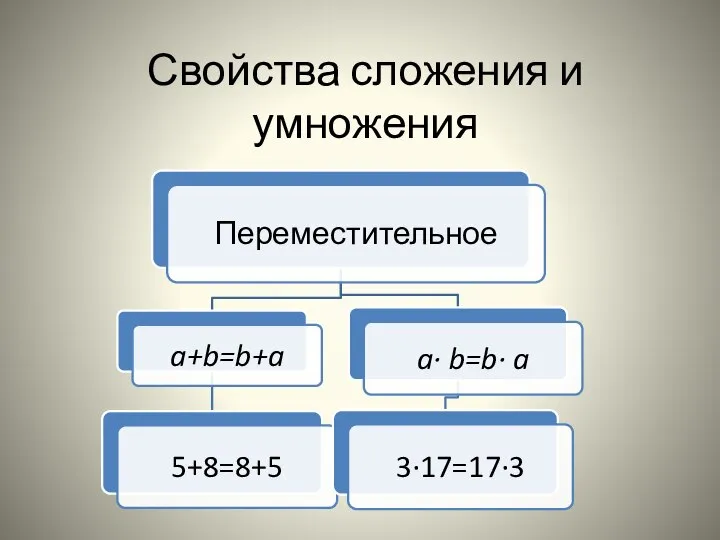 Свойства сложения и умножения. 5 класс
Свойства сложения и умножения. 5 класс ГИА 2014. Модуль Геометрия №10
ГИА 2014. Модуль Геометрия №10 Муниципальное бюджетное общеобразовательное учреждение «Дрезненская гимназия» ШУТКА ГЕНИЕВ: ФЛЕКСАГОН Выполнила: Маркина Диа
Муниципальное бюджетное общеобразовательное учреждение «Дрезненская гимназия» ШУТКА ГЕНИЕВ: ФЛЕКСАГОН Выполнила: Маркина Диа Decision trees. Деревья решений
Decision trees. Деревья решений Формула Ньютона-Лейбница
Формула Ньютона-Лейбница 7 класста алгебра курсы буенча кабатлау дәресе
7 класста алгебра курсы буенча кабатлау дәресе Подготовка к ЕГЭ (профильный уровень). Задания 5
Подготовка к ЕГЭ (профильный уровень). Задания 5 Четырехугольники
Четырехугольники Планиметрия. Задачи на доказательство
Планиметрия. Задачи на доказательство Показательная и логарифмическая функции
Показательная и логарифмическая функции Смешанные числа 5. класс
Смешанные числа 5. класс Векторы и координаты. Решение задач. Основные понятия комбинаторики
Векторы и координаты. Решение задач. Основные понятия комбинаторики Призма
Призма Дискретная математика. Основные понятия теории множеств. (Лекция 1.1)
Дискретная математика. Основные понятия теории множеств. (Лекция 1.1) Математикалық ұғымдарды
Математикалық ұғымдарды Числовые и буквенные выражения. Математика 5 класс
Числовые и буквенные выражения. Математика 5 класс Возведение степени в степень
Возведение степени в степень Задания по математике (5 класс, часть 1)
Задания по математике (5 класс, часть 1) Задачи на проценты. ЕГЭ
Задачи на проценты. ЕГЭ Обработка данных. Задачи локального и глобального интерполирования
Обработка данных. Задачи локального и глобального интерполирования Физические величины
Физические величины