Возрастание и убывание функции. Рано или поздно всякая правильная математическая идея находит применение в том или ином деле. А.Н.

Числовые промежутки

[α;b] – отрезок
(α;b) – интервал
(α;b] – полуинтервал
[α;b) - полуинтервал

Функция f(x) называется возрастающей на некотором промежутке, если большему значению аргумента

Функция f(x) называется убывающей на некотором промежутке, если большему значению аргумента

Теорема Лагранжа

Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема

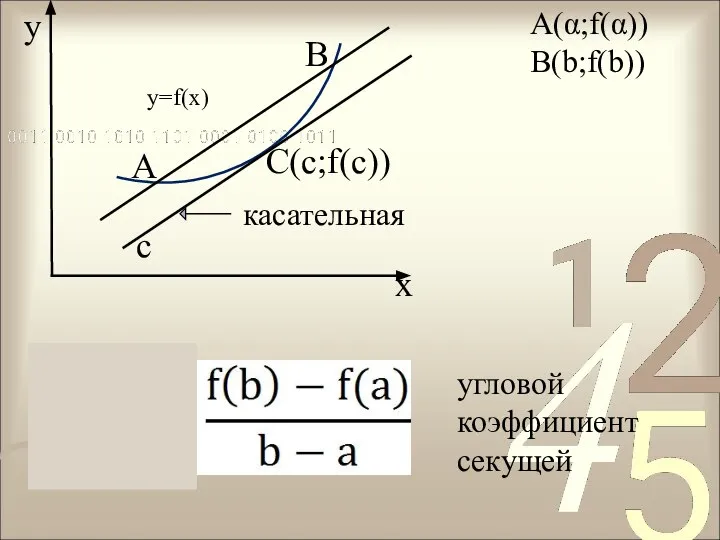
y

x

A

B

касательная

с

A(α;f(α))
B(b;f(b))

y=f(x)

угловой коэффициент секущей

C(c;f(с))

Достаточные условия возрастания и убывания функции

Пусть функция f(х) непрерывна на