Задача оптимизации. Проектные параметры

Сентябрь 13, 2022

Главная
Математика
Задача оптимизации. Проектные параметры

Содержание

2. Задача оптимизации. Проектные параметры Оптимизация – это процесс выбора наилучшего варианта из всех возможных. В инженерных
3. Задача оптимизации. Целевая функция Выбор оптимального решения или сравнение альтернатив производится с помощью целевой функции f(x1,
4. Безусловная и условная оптимизация Существует два типа задач оптимизации: безусловные и условные. Безусловная оптимизация – это
5. Пример постановки задачи оптимизации
6. Пример постановки задачи оптимизации
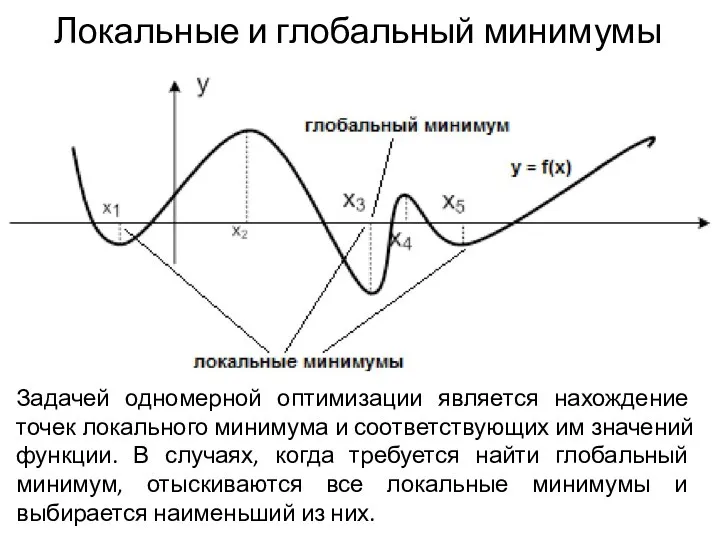
7. Локальные и глобальный минимумы Задачей одномерной оптимизации является нахождение точек локального минимума и соответствующих им значений
8. Унимодальные функции Отрезок, на котором локализован единственный минимум, называется отрезком неопределенности. Все численные методы одномерной оптимизации
9. Условия унимодальности функции Обычно при решении задачи одномерной оптимизации речь идет о поиске единственного экстремума функции.
10. График функции f(x) = x3 – x + e-x
11. Пример проверки условий унимодальности
12. Аналитический метод отыскания локального минимума
13. Методы поиска Для численного решения задачи безусловной одномерной оптимизации используются различные методы поиска. Их сущность состоит
14. Методы поиска
15. Методы сканирования (прямого перебора)
16. Схема алгоритма метода прямого перебора с переменным шагом
17. Методы последовательного поиска
18. Метод деления отрезка пополам
19. Сущность метода деления отрезка пополам
20. Свойства метода деления отрезка пополам
22. Скачать презентацию

Слайд 2

Задача оптимизации. Проектные параметры
Оптимизация – это процесс выбора наилучшего варианта из

всех возможных. В инженерных расчетах методы оптимизации позволяют выбрать наилучший вариант конструкции, распределения ресурсов и т.п. В экономических расчетах – получить максимальную прибыль, добиться минимальных затрат и т.п.
В процессе решения задачи оптимизации необходимо найти оптимальные значения проектных параметров (параметров плана), определяющих данную задачу: x1, x2, … xn. Содержательный смысл этих параметров зависит от конкретной задачи. Это могут быть линейные размеры, масса, температура и тому подобные параметры оптимизируемого объекта. Число n характеризует размерность задачи оптимизации.

Слайд 3

Задача оптимизации. Целевая функция
Выбор оптимального решения или сравнение альтернатив производится с

помощью целевой функции f(x1, x2, … xn), зависящей от проектных параметров. Решение задачи оптимизации заключается в отыскании таких значений проектных параметров, при которых достигается минимум или максимум целевой функции. Примерами целевых функций могут служить мощность установки, прочность конструкции, объем выпуска продукции, стоимость перевозки грузов, прибыль и т.п.
Геометрически целевая функция представляет собой поверхность в (n+1)–мерном пространстве. В частности, при n=1 это кривая на плоскости y=f(x); при n=2 – поверхность в 3–мерном пространстве y = f(x1, x2).

Слайд 4

Безусловная и условная оптимизация
Существует два типа задач оптимизации: безусловные и условные.
Безусловная

оптимизация – это отыскание минимума (максимума) функции и определение соответствующих значений аргументов в n–мерном пространстве без каких–либо ограничений на значения аргументов. Обычно рассматриваются задачи минимизации, так как задача отыскания максимума легко сводится к задаче минимизации путем замены знака целевой функции на противоположный.
При условной оптимизации задача имеет ограничения, определяющие множество S в n–мерном пространстве, в пределах которого ищется оптимальное решение. Эти ограничения задаются совокупностью некоторых функций gi(x1, x2, … xn); i=1, 2, …m, удовлетворяющих уравнениям или неравенствам:
gi(x1, x2, … xn) >= 0; i=1, 2, …m
Теория и методы решения задач условной оптимизации – предмет исследования важного раздела прикладной математики – математического программирования.

Слайд 5

Пример постановки задачи оптимизации

Слайд 6

Пример постановки задачи оптимизации

Слайд 7

Локальные и глобальный минимумы
Задачей одномерной оптимизации является нахождение точек локального минимума

и соответствующих им значений функции. В случаях, когда требуется найти глобальный минимум, отыскиваются все локальные минимумы и выбирается наименьший из них.

Слайд 8

Унимодальные функции
Отрезок, на котором локализован единственный минимум, называется отрезком неопределенности. Все

численные методы одномерной оптимизации применяются только для функций, унимодальных на отрезке неопределенности. Функция f(x) называется унимодальной на отрезке [a;b], если она имеет на этом отрезке единственный минимум в точке x*, и f(x) строго возрастает при x< x* и x> x*. При этом возможны три случая.

Слайд 9

Условия унимодальности функции
Обычно при решении задачи одномерной оптимизации речь идет о

поиске единственного экстремума функции. В этом случае необходимым условием унимодальности функции и существования экстремума является неубывание первой производной f'(x) на отрезке неопределенности [a;b]. Достаточным условием является положительный знак второй производной f''(x)>0 на отрезке неопределенности [a;b].

Слайд 10

График функции f(x) = x3 – x + e-x

Слайд 11

Пример проверки условий унимодальности

Слайд 12

Аналитический метод отыскания локального минимума

Слайд 13

Методы поиска
Для численного решения задачи безусловной одномерной оптимизации используются различные методы

поиска. Их сущность состоит в последовательном сужении отрезка неопределенности. Вначале длина отрезка равна b0–a0, а в итоге она должна стать меньше заданной допустимой погрешности решения ε, так что х*ϵ[an;bn], причем bn - an < ε.
За приближенное значение точки минимума ẍ может быть принята любая точка отрезка [an;bn], при этом |ẍ - х*| <= bn - an < ε. Обычно принимают ẍ = (an+bn)/2, то есть середину отрезка.

Слайд 14

Методы поиска

Слайд 15

Методы сканирования (прямого перебора)

Слайд 16

Схема алгоритма метода прямого перебора с переменным шагом

Слайд 17

Методы последовательного поиска

Слайд 18

Метод деления отрезка пополам

Слайд 19

Сущность метода деления отрезка пополам

Слайд 20

Задача оптимизации. Проектные параметры

Содержание

Задача оптимизации. Проектные параметрыОптимизация – это процесс выбора наилучшего варианта из

Задача оптимизации. Целевая функцияВыбор оптимального решения или сравнение альтернатив производится с

Безусловная и условная оптимизацияСуществует два типа задач оптимизации: безусловные и условные.Безусловная

Пример постановки задачи оптимизации

Пример постановки задачи оптимизации

Локальные и глобальный минимумыЗадачей одномерной оптимизации является нахождение точек локального минимума

Унимодальные функцииОтрезок, на котором локализован единственный минимум, называется отрезком неопределенности. Все

Условия унимодальности функцииОбычно при решении задачи одномерной оптимизации речь идет о

График функции f(x) = x3 – x + e-x

Пример проверки условий унимодальности

Аналитический метод отыскания локального минимума

Методы поискаДля численного решения задачи безусловной одномерной оптимизации используются различные методы

Методы поиска

Методы сканирования (прямого перебора)

Схема алгоритма метода прямого перебора с переменным шагом

Методы последовательного поиска

Метод деления отрезка пополам

Сущность метода деления отрезка пополам

Свойства метода деления отрезка пополам

Похожие презентации

Задача оптимизации. Проектные параметры
Оптимизация – это процесс выбора наилучшего варианта из

Задача оптимизации. Целевая функция
Выбор оптимального решения или сравнение альтернатив производится с

Безусловная и условная оптимизация
Существует два типа задач оптимизации: безусловные и условные.
Безусловная

Локальные и глобальный минимумы
Задачей одномерной оптимизации является нахождение точек локального минимума

Унимодальные функции
Отрезок, на котором локализован единственный минимум, называется отрезком неопределенности. Все

Условия унимодальности функции
Обычно при решении задачи одномерной оптимизации речь идет о

Методы поиска
Для численного решения задачи безусловной одномерной оптимизации используются различные методы