Содержание
- 2. Золотое сечение – гармоническая пропорция В математике пропорцией (лат. proportio) называют равенство двух отношений: a :
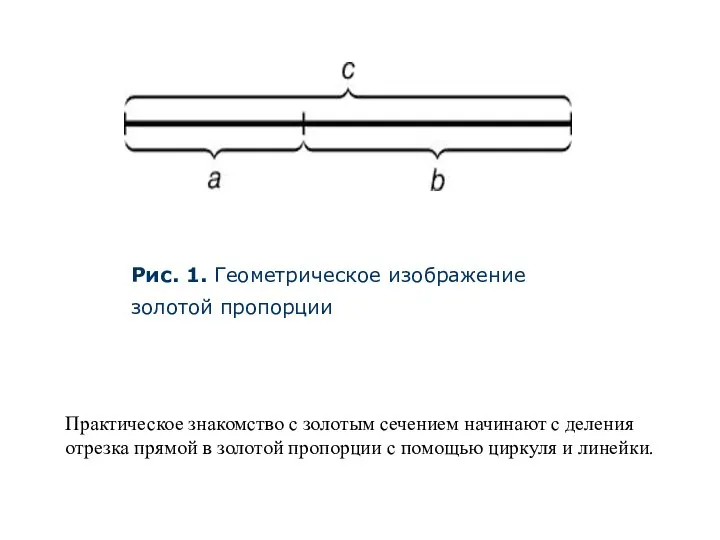
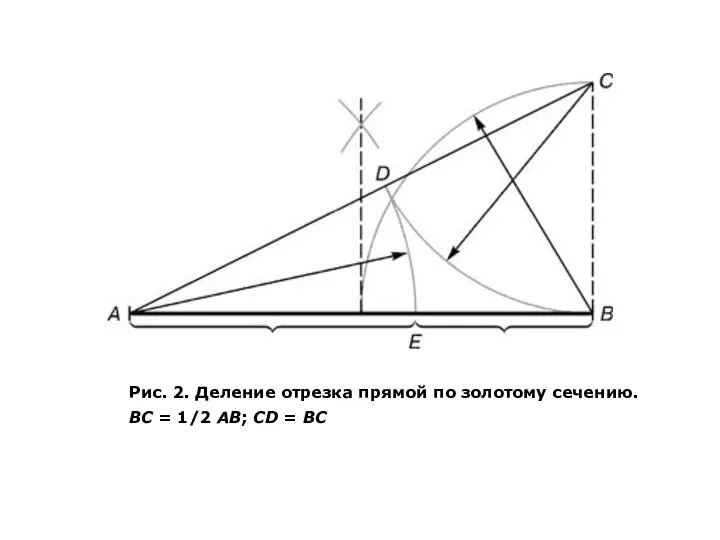
- 3. Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении. Золотое сечение –
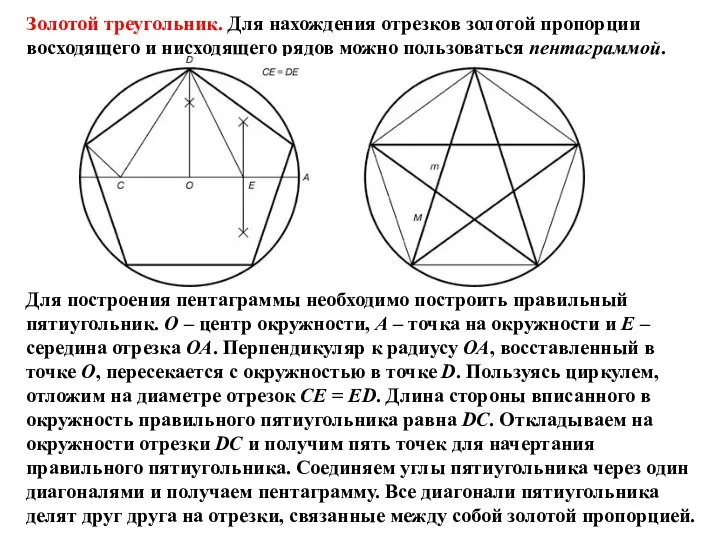
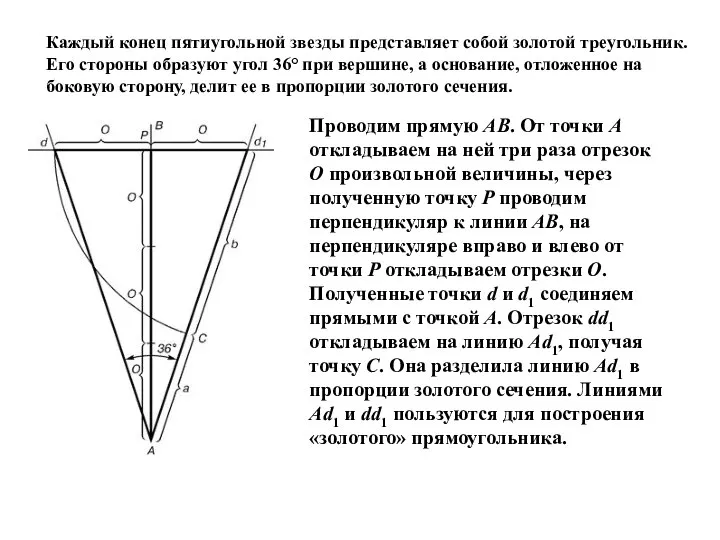
- 10. Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а
- 11. Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик
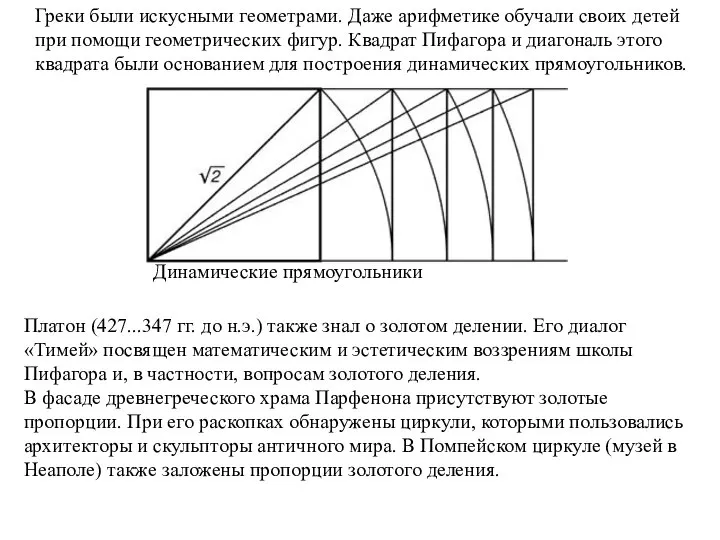
- 12. Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и
- 13. Примеры золотого сечения в древнегреческом искусстве
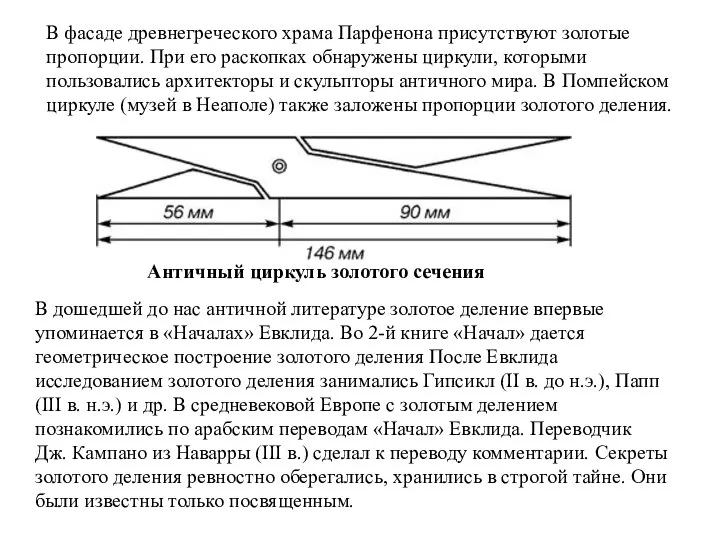
- 14. В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы
- 15. В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников. Особенно это проявилось в
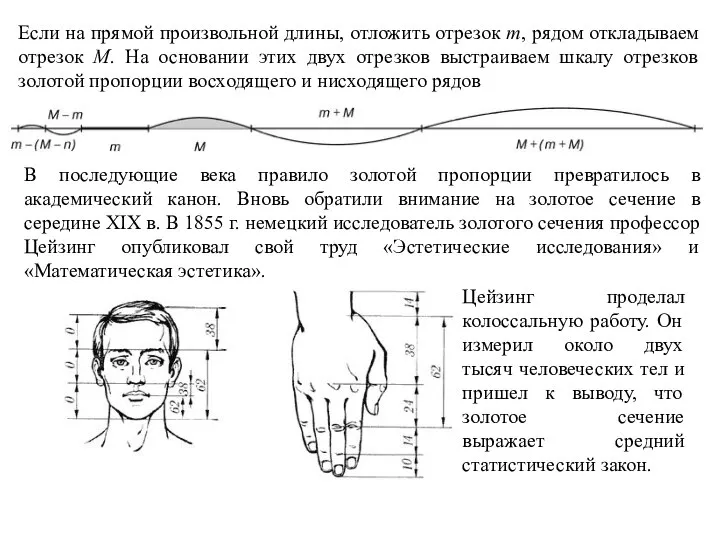
- 16. Если на прямой произвольной длины, отложить отрезок m, рядом откладываем отрезок M. На основании этих двух
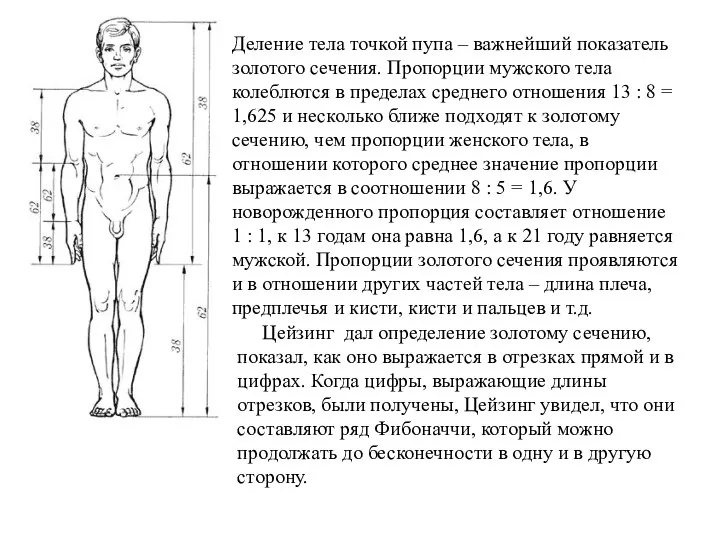
- 17. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего
- 18. Ряд Фибоначчи С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо, более известного
- 19. Обобщенное золотое сечение Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство,
- 20. Раковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая
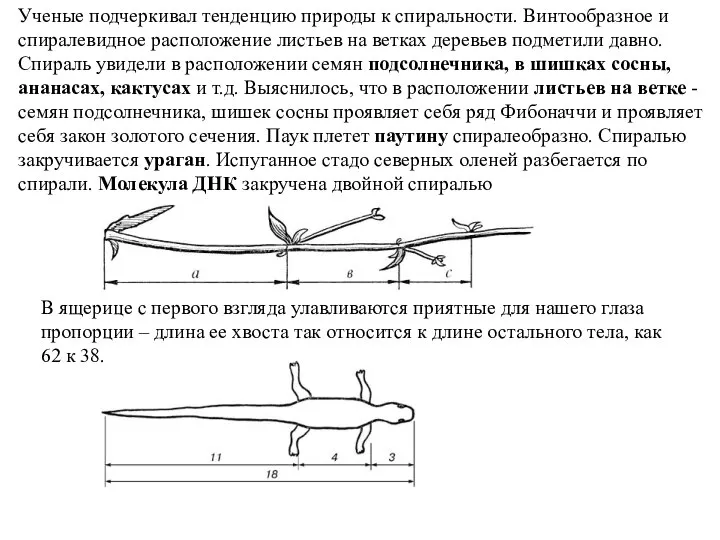
- 21. Ученые подчеркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно.
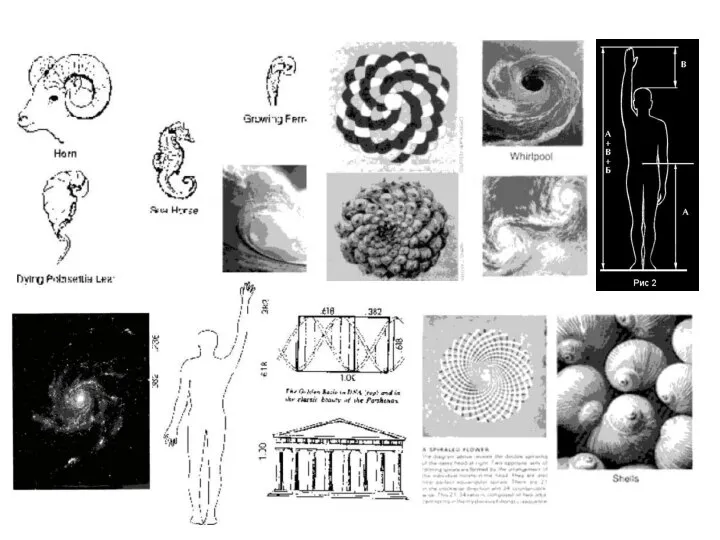
- 22. И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы – симметрия относительно направления
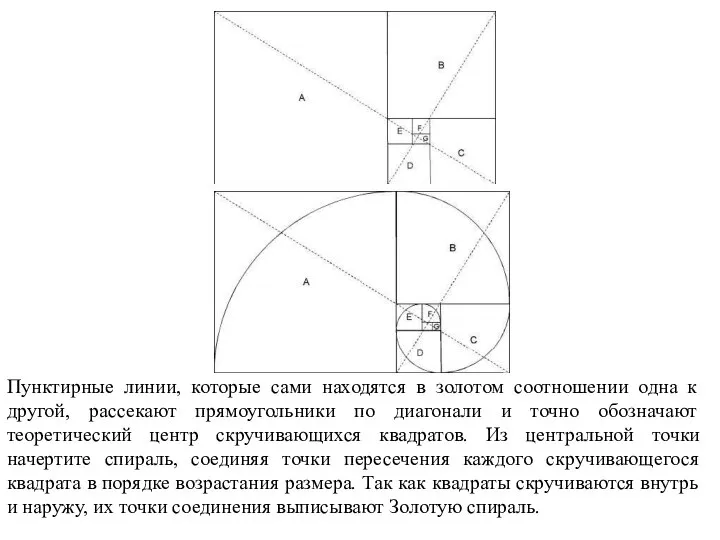
- 23. Золотой прямоугольник Стороны Золотого прямоугольника находятся в пропорции 1.618 к 1. Чтобы построить Золотой прямоугольник, начните
- 24. Пунктирные линии, которые сами находятся в золотом соотношении одна к другой, рассекают прямоугольники по диагонали и
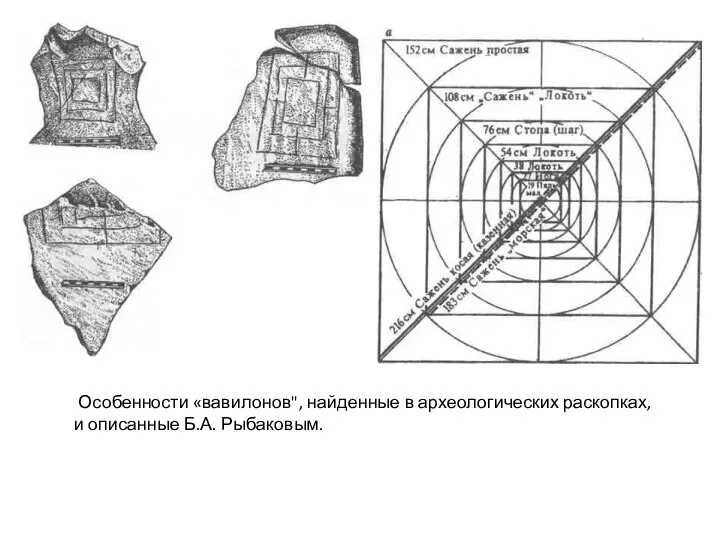
- 26. Особенности «вавилонов", найденные в археологических раскопках, и описанные Б.А. Рыбаковым.
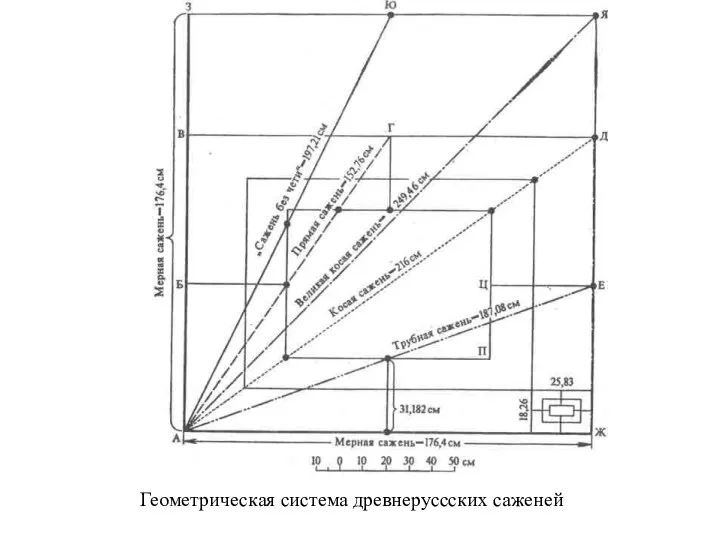
- 27. Геометрическая система древнеруссских саженей
- 28. План церкви Успения в Старой Ладоге. Мерный ангел живого квадрата на плане церкви Успения [18]предлагаемого плана.
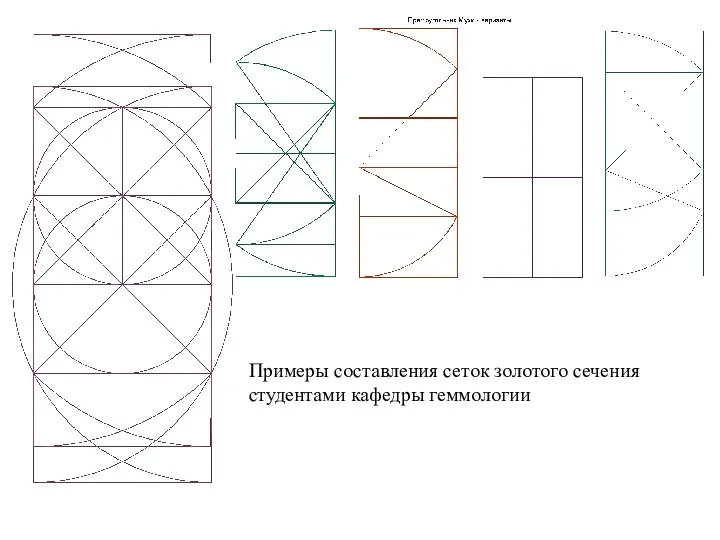
- 29. Примеры составления сеток золотого сечения студентами кафедры геммологии
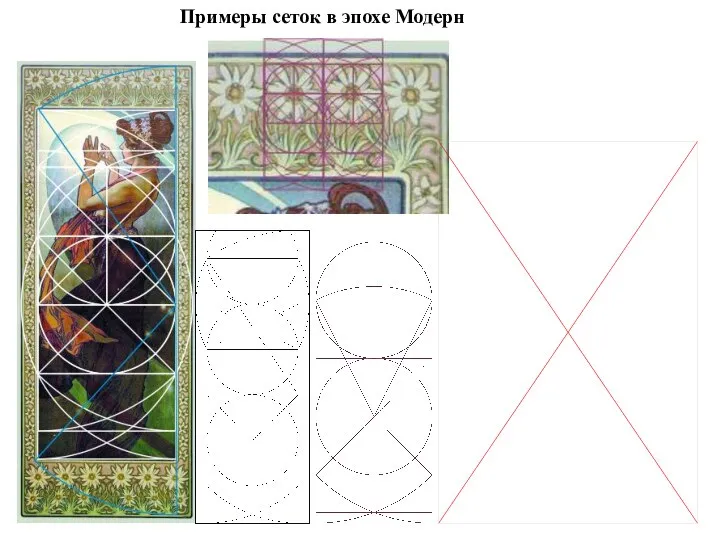
- 30. Примеры сеток в эпохе Модерн
- 32. Скачать презентацию












![План церкви Успения в Старой Ладоге. Мерный ангел живого квадрата на плане церкви Успения [18]предлагаемого плана.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1464031/slide-27.jpg)
 Разложение вектора по двум неколлинеарным векторам
Разложение вектора по двум неколлинеарным векторам Аксонометрические проекции
Аксонометрические проекции Потоки событий. Марковские случайные процессы
Потоки событий. Марковские случайные процессы Элементы комбинаторики (обобщающий урок). 9 класс
Элементы комбинаторики (обобщающий урок). 9 класс Приведите примеры применения линейной функции в смежных предметах
Приведите примеры применения линейной функции в смежных предметах Бенефис линейной функции
Бенефис линейной функции Функции многих переменных
Функции многих переменных «СПОСОБЫ СОСТАВЛЕНИЯ И МЕТОДЫ РЕШЕНИЯ ЛОГИЧЕСКИХ ЗАДАЧ» Работу выполнила Ученица 8 класса МБОУ «Гим
«СПОСОБЫ СОСТАВЛЕНИЯ И МЕТОДЫ РЕШЕНИЯ ЛОГИЧЕСКИХ ЗАДАЧ» Работу выполнила Ученица 8 класса МБОУ «Гим Лекция 7. Корреляционный анализ
Лекция 7. Корреляционный анализ Прогрессия. Задача
Прогрессия. Задача Умножение и деление на 8
Умножение и деление на 8 Сложение и вычитание десятичных дробей. Аль-Каши Джемшид Ибн Масуд
Сложение и вычитание десятичных дробей. Аль-Каши Джемшид Ибн Масуд Тренировочные задания В2 (графическое представление данных)
Тренировочные задания В2 (графическое представление данных) Математика и космос. Над проектом работали учащиеся 7 класса Лесхозовской ООШ под руководством Джамалдиновой З.Ш
Математика и космос. Над проектом работали учащиеся 7 класса Лесхозовской ООШ под руководством Джамалдиновой З.Ш  Презентация на тему Средняя линия трапеции
Презентация на тему Средняя линия трапеции Сравнение чисел
Сравнение чисел Отрезок. Измерение отрезков
Отрезок. Измерение отрезков Сопряжение. Центр сопряжения. Точки сопряжения
Сопряжение. Центр сопряжения. Точки сопряжения Тела вращения
Тела вращения Сложение, вычитание многочленов и умножение на одночлен
Сложение, вычитание многочленов и умножение на одночлен Свойства квадратного корня
Свойства квадратного корня Прямая и плоскость в пространстве
Прямая и плоскость в пространстве Основы логики. Импликация
Основы логики. Импликация Проект по математике. Число и цифра 7
Проект по математике. Число и цифра 7 Длины оснований трапеций. Создание программы
Длины оснований трапеций. Создание программы Уравнения высших степеней (корни многочлена от одной переменной)
Уравнения высших степеней (корни многочлена от одной переменной) ЭГЕ по математике. Прототип 18. Задачи с параметром. Применение свойств функции
ЭГЕ по математике. Прототип 18. Задачи с параметром. Применение свойств функции Свойства числовых неравенств. (8 класс)
Свойства числовых неравенств. (8 класс)