Содержание
- 2. Потоки событий Это последовательность событий происходящих одно за другим в определенные интервалы времени. T - средняя
- 3. Потоки событий Стационарный Количество событий, попадающих на любой произвольный интервал времени τ не зависит от положения
- 4. Потоки событий Ординарный В любой момент времени происходит одно и только одно событие, т. е. вероятность
- 5. Экономическое применение Современные финансово – банковские операции предполагают погашение задолженности в рассрочку, периодическое поступление доходов от
- 6. Задача Для анализа изменения с течением времени размера текущего фонда банка, занимающегося выдачей долгосрочных ссуд, важно
- 7. Решение По условию задачи поток выплат можно считать простейшим с интенсивностью λ=2 (за неделю). Следовательно, число
- 8. Решение Пусть X(τ) - дискретная случайная величина , представляющая собой число выплат, поступивших за промежуток времени
- 9. Решение Пусть непрерывная случайная величина T - промежуток времени между двумя любыми соседними выплатами (событиями простейшего
- 10. Задачи для самостоятельного решения 1. Обычно студент приходит на остановку ровно в 8 часов утра и,
- 11. Задачи для самостоятельного решения 2. Поток заявок, поступающих в некоторую систему массового обслуживания, достаточно точно моделируется
- 12. Марковские случайные процессы
- 13. Основные понятия Под системой S будем понимать всякое целостное множество взаимосвязанных элементов, которое нельзя расчленить на
- 14. Основные понятия В случае дискретного множества состояний система меняет свои состояния скачком (мгновенно). В случае же
- 15. А. А. Марков (1856 - 1922) Андрей Андреевич Марков - старший - выдающийся русский математик, разработавший
- 16. Виды Марковских процессов Дискретные состояния и дискретное время (цепь Маркова) Непрерывные состояния и дискретное время (Марковские
- 17. Марковские цепи Цепью Маркова называют такую последовательность случайных событий, в которой вероятность каждого события зависит только
- 18. Задание Марковской цепи множеством состояний S = {s1, …, sn}, событием является переход из одного состояния
- 19. Пример S = {S1, …, S5} p(0) = {1, 0, 0, 0, 0}
- 20. Пример
- 21. Виды Марковских цепей Марковская цепь называется однородной, если переходные вероятности от времени не зависят, то есть
- 22. Цель моделирования определить вероятность системы находится в j-ом состоянии после k-го шага. Обозначим эту вероятность однородная
- 23. Задача №1 Некоторая совокупность рабочих семей поделена на три группы: ε1 – семьи, не имеющие автомашины
- 24. Задача №1 Найти: а)вероятность того, что семья, не имевшая машины и не собиравшаяся ее приобрести, будет
- 25. Решение задачи №1 а) Дано: т.е. вектор начальных вероятностей p(0)=(1,0,0) (сейчас система в состоянии 1) Найти:
- 26. Решение задачи №1 Получим вектор вероятностей через 1 год В нашем случае это 1-ая строка матрицы
- 27. Решение задачи №1 Вычисления: Ответ: вероятность того, что семья, не имевшая машины и не собиравшаяся ее
- 28. Задача №2 Предположим, что некая фирма осуществляет доставку оборудования по Москве: в северный округ (обозначим А),
- 29. Задача №2 Если курьер стартует из центрального округа, какова вероятность того, что осуществив две доставки, он
- 30. Предельные вероятности Для эргодических цепей при достаточно большом времени функционирования (t стремится к бесконечности) наступает стационарный
- 31. Предельные вероятности Пусть xi – предельные вероятности (i=1..n), где n – число состояний. Тогда xi являются
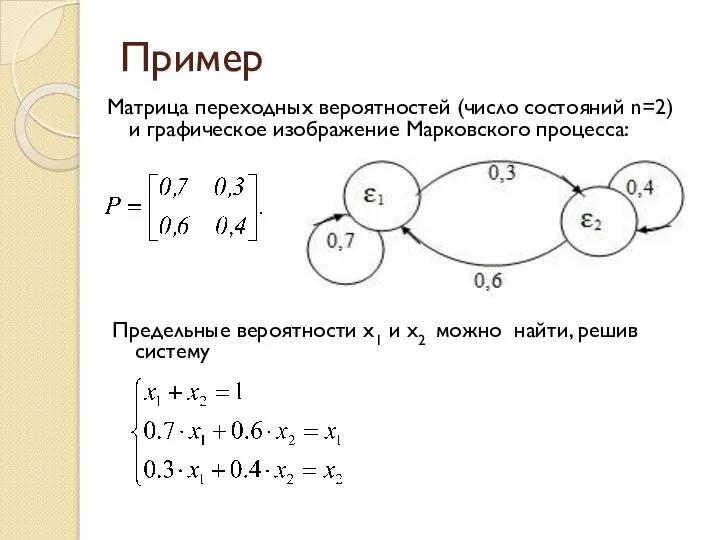
- 32. Пример Матрица переходных вероятностей (число состояний n=2) и графическое изображение Марковского процесса: Предельные вероятности x1 и
- 33. Задача №3 Две машины А и В сдаются в аренду по одной и той же цене.
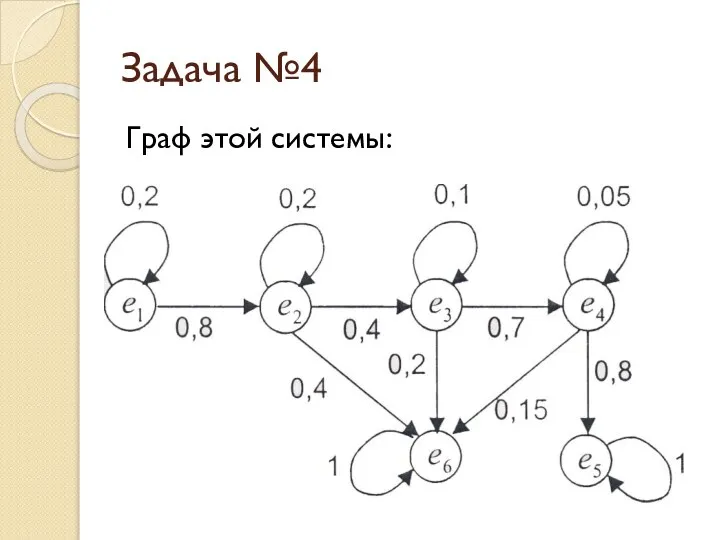
- 34. Задача №4 Посетитель банка с намерением получить кредит проходит ряд проверок (состояний): е1 – оформление документов;
- 35. Задача №4 Граф этой системы:
- 37. Скачать презентацию
































 Площадь треугольника и подобие
Площадь треугольника и подобие Осевая и центральная симметрии
Осевая и центральная симметрии Введение в математическую логику и теорию алгоритмов
Введение в математическую логику и теорию алгоритмов Параллелепипед и тетраэдр
Параллелепипед и тетраэдр Равнобедренный треугольник
Равнобедренный треугольник Презентация по математике "Повторение курса математики." - скачать бесплатно
Презентация по математике "Повторение курса математики." - скачать бесплатно Алгебра і початки аналізу
Алгебра і початки аналізу Применение интегралов
Применение интегралов Логическая закономерность, лежащая в основе подбора алгебраических дробей
Логическая закономерность, лежащая в основе подбора алгебраических дробей Дәрәҗәнең үзлекләре
Дәрәҗәнең үзлекләре Решение задач на нахождение площади МОУ ООШ с.Ст.Турдаки Демидова Людмила Анатольевна
Решение задач на нахождение площади МОУ ООШ с.Ст.Турдаки Демидова Людмила Анатольевна Симметрия в жизни
Симметрия в жизни Презентация по математике "Дистанционное обучение. За и против." - скачать бесплатно
Презентация по математике "Дистанционное обучение. За и против." - скачать бесплатно Вариационный ряд, таблицы сопряженности признаков и проверка гипотез
Вариационный ряд, таблицы сопряженности признаков и проверка гипотез Уравнения, 5 класс.
Уравнения, 5 класс.  Тетраэдр и его сечение
Тетраэдр и его сечение У бабусі. Математичний диктант-казка
У бабусі. Математичний диктант-казка Көбейту және бөлуді пысықтау
Көбейту және бөлуді пысықтау Арифметическая прогрессия
Арифметическая прогрессия Золотое сечение в искусстве
Золотое сечение в искусстве Синус, косинус и тангенс (решение задач)
Синус, косинус и тангенс (решение задач) Кореляционный анализ
Кореляционный анализ Первый признак подобия треугольников. Решение задач
Первый признак подобия треугольников. Решение задач Геометрический смысл производной. Задачи типа В8 в ЕГЭ
Геометрический смысл производной. Задачи типа В8 в ЕГЭ Формулы. Урок изучения нового материала
Формулы. Урок изучения нового материала Таблица умножения и деления с числом
Таблица умножения и деления с числом Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся
Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся Сложение и вычитание 1 класс
Сложение и вычитание 1 класс