Содержание
- 2. Рассмотрим случай, когда одно и то же испытание повторяется несколько раз - проводится серия испытаний в
- 3. Примеры независимых испытаний 1. Несколько последовательных бросаний монеты. 2. Несколько последовательных выниманий карты из колоды, при
- 4. Пусть в результате случайного испытания может произойти или не произойти событие А. Если событие наступило, назовём
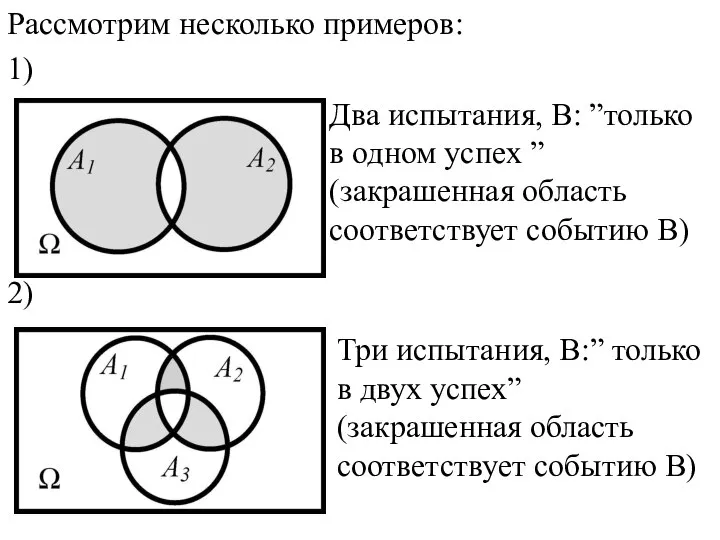
- 5. Рассмотрим несколько примеров: 1) 2)
- 11. По классическому определению вероятности: Таких испытаний по условию производится 4. Тогда вероятность, что в 4-х независимых
- 12. Используя т. сложения несовместных событий: Рассмотрим следующий пример, когда из двух очень похожих вопросов на один
- 13. Пример. Система радиолокационных станций ведет наблюдение за группой объектов, состоящей из 8 единиц. Каждый объект может
- 15. Наивероятнейшее число появлений события в независимых испытаниях Число k0 (наступление события в независимых испытаниях, в каждом
- 16. а) если число (np – q) – дробное, то существует одно наивероятнейшее число k0; б) если
- 17. Пример. В урне 10 белых и 40 чёрных шаров. Вынимают подряд 14 шаров, причём цвет вынутого
- 18. Пример. Вероятность попадания стрелком в цель равна 0,7. Сделано 25 выстрелов. Определить наивероятнейшее число попаданий в
- 19. Пример. Два равносильных шахматиста играют в шахматы. Что вероятнее – выиграть две партии из 4-х или
- 22. б) каждое испытание имеет три, а не два исхода: выпадение тройки, выпадение единицы, выпадение остальных граней.
- 24. Формула Пуассона В том случае, когда вероятность появления события p мала ( p Значения при фиксированных
- 26. Пример. Вероятность искажения одного символа при передаче сообщения по линии связи равна 0,001. Сообщение считают принятым,
- 27. успех: символ не искажается, р = 0,001 -вероятность успеха; m = 0 Вычислим λ = np
- 28. Пример. Известно, что процент брака для некоторой детали равен 0,5%. Контролер проверяет 1000 деталей. Какова вероятность
- 29. Ответ: вероятность обнаружить ровно 3 бракованные детали равна 0,14; обнаружить не менее 3-х бракованных деталей 0,875.
- 30. Пример (задача С. Пепайса). Пепайс предложил Ньютону следующую задачу. Какое из событий более вероятно: A =
- 34. Скачать презентацию





























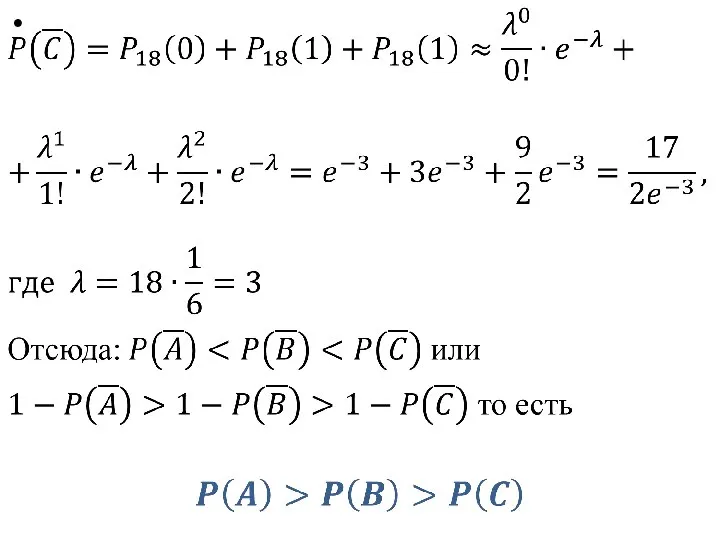
 20171101_prezentatsiya_01
20171101_prezentatsiya_01 20160828_izuchenie_ustnyy_schet_tema_sravnenie_drobey_5_kl_nikolskiy
20160828_izuchenie_ustnyy_schet_tema_sravnenie_drobey_5_kl_nikolskiy Специальные виды тяжелого бетона
Специальные виды тяжелого бетона Сбалансированное питание
Сбалансированное питание Оболочки отрицательной гауссовой кривизны
Оболочки отрицательной гауссовой кривизны The history of the mustang
The history of the mustang Католичество. Иерархическая структура
Католичество. Иерархическая структура Здравствуй Новый Год!
Здравствуй Новый Год! Слово и слог. Закрепление
Слово и слог. Закрепление Сварочное производство
Сварочное производство Лекция 13. Пластмассы, как материал для строительных конструкций. Основные виды конструкционных пластмасс и области их применения
Лекция 13. Пластмассы, как материал для строительных конструкций. Основные виды конструкционных пластмасс и области их применения Работа с презентациями
Работа с презентациями Обработка поясных изделий
Обработка поясных изделий По технологии программирования
По технологии программирования Энергетические ресурсы в контексте технологического прогресса и геополитики
Энергетические ресурсы в контексте технологического прогресса и геополитики Способы прокладки кабелей в подземных горных выработках
Способы прокладки кабелей в подземных горных выработках С чего начинается доброта?
С чего начинается доброта? Создание буклета
Создание буклета 20120612_pesnya_dusha_naroda
20120612_pesnya_dusha_naroda Робот – помощник
Робот – помощник Поздравление с днём рождения
Поздравление с днём рождения Rekreasyon. Ders notlari
Rekreasyon. Ders notlari Сланцевая революция и ее международно-политические последствия
Сланцевая революция и ее международно-политические последствия 20131222_russkaya_ikona
20131222_russkaya_ikona Легкие стальные тонкостенные конструкции
Легкие стальные тонкостенные конструкции 20170618_sobor_vasiliya_blazhennogo
20170618_sobor_vasiliya_blazhennogo Своя Игра
Своя Игра Чистая планета — премиальная бытовая химия в розлив
Чистая планета — премиальная бытовая химия в розлив