Содержание
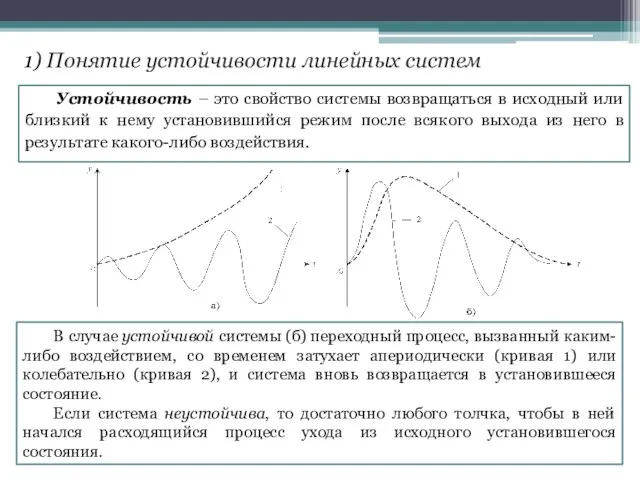
- 2. . 1) Понятие устойчивости линейных систем Устойчивость – это свойство системы возвращаться в исходный или близкий
- 3. . Устойчивую систему можно определить также как систему, переходные процессы в которой являются затухающими. Приведенное понятие
- 4. - общее решение уравнения (1) без правой части, т. е. с правой частью, равной нулю (свободная
- 5. . Общее решение однородного уравнения в случае простых (различных) корней характеристического уравнения можно записать 1) Понятие
- 6. . Необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части. Условием устойчивости системы
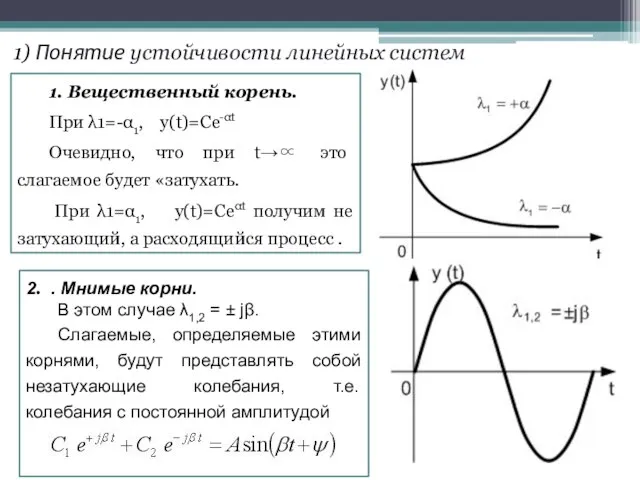
- 7. . 1. Вещественный корень. При λ1=-α1, y(t)=Ce-αt Очевидно, что при t→∝ это слагаемое будет «затухать. При
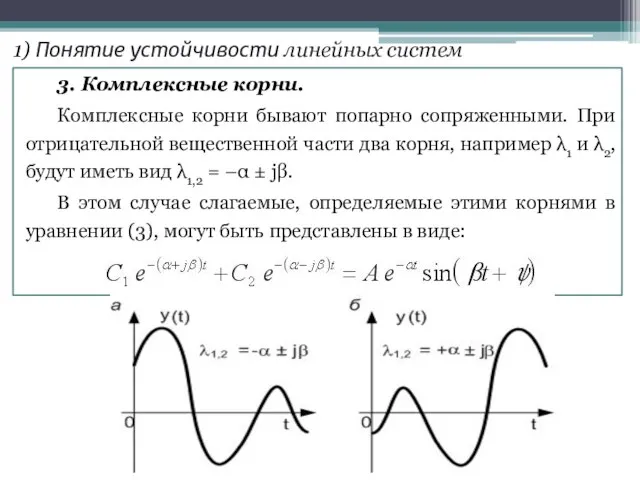
- 8. . 3. Комплексные корни. Комплексные корни бывают попарно сопряженными. При отрицательной вещественной части два корня, например
- 9. . 1) Понятие устойчивости линейных систем
- 10. Различают два основных типа границы устойчивости: 1) наличие нулевого корня; 2) наличие пары чисто мнимых корней.
- 11. Для суждения об устойчивости системы практически не требуется находить корней ее характеристического уравнения в связи с
- 12. – Критерий устойчивости Гурвица 2) Алгебраические критерии устойчивости Пусть имеем характеристический полином вида Полагаем, что Составим
- 13. Правила построения матрицы Гурвица: Первая строка содержит все нечетные коэффициенты до последнего, после чего строка заполняется
- 14. Условие устойчивости заключается в требовании положительности определителя Гурвица и всех его диагональных миноров. 2) Алгебраические критерии
- 15. 2) Алгебраические критерии устойчивости Для n = 3 Условия устойчивости сводятся к неравенствам: (10) (11) Для
- 16. Критерий устойчивости Гурвица в общем виде сводится к тому, что при положительности коэффициента при старшей степени
- 17. 2) Алгебраические критерии устойчивости Рассмотрим замкнутую систему Характеристический полином замкнутой системы имеет вид Матрица Гурвица
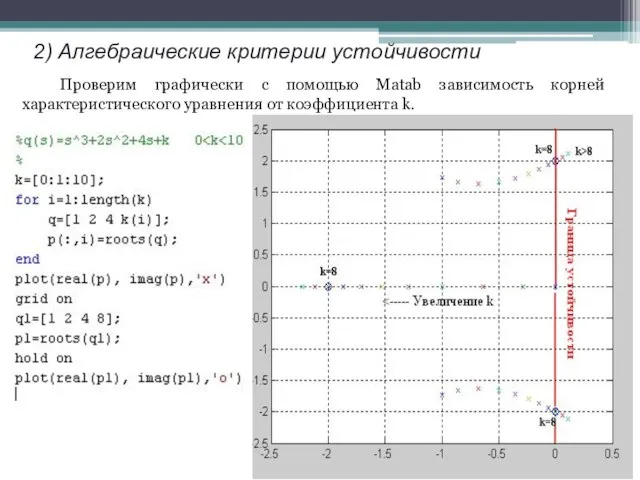
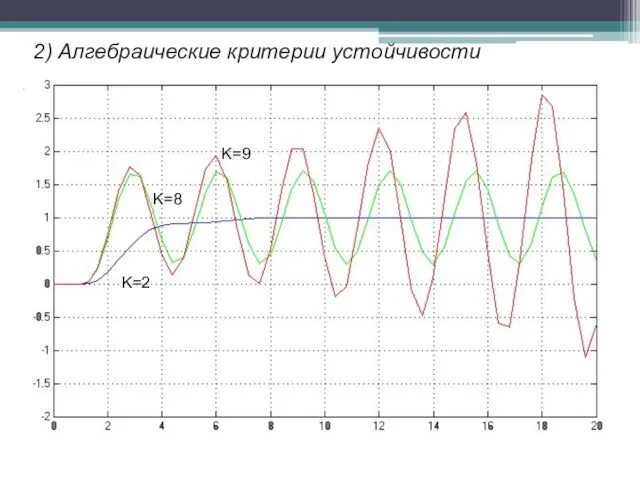
- 18. 2) Алгебраические критерии устойчивости Проверим графически с помощью Matab зависимость корней характеристического уравнения от коэффициента k.
- 19. 2) Алгебраические критерии устойчивости K=2 K=8 K=9
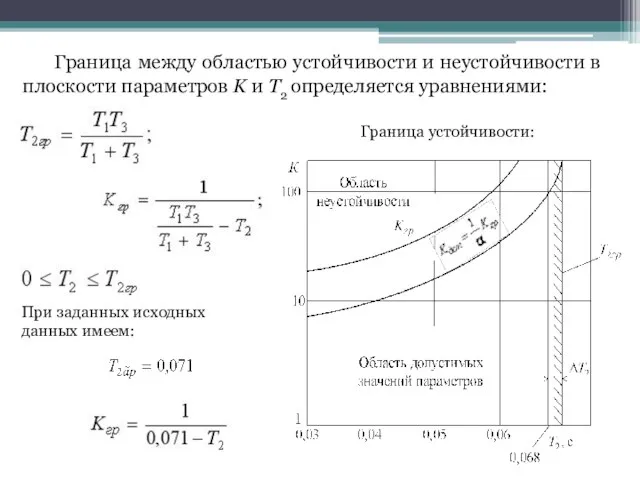
- 20. 2) Алгебраические критерии устойчивости Пример 2. Используя критерий Гурвица построить область устойчивости в плоскости параметров (K,
- 21. Граница между областью устойчивости и неустойчивости в плоскости параметров K и T2 определяется уравнениями: При заданных
- 22. 2) Алгебраические критерии устойчивости Система будет устойчивой при любых настройках и любых значениях K, лежащих ниже
- 23. Пример 3. Используя критерий Гурвица построить область устойчивости в плоскости параметров (K2, T2) при следующих данных:
- 24. Главная передаточная функция замкнутой системы Характеристическое уравнение функции имеет вид
- 25. Определитель Гурвица для системы 3– го порядка имеет вид Условия устойчивости замкнутой системы запишем следующим образом:
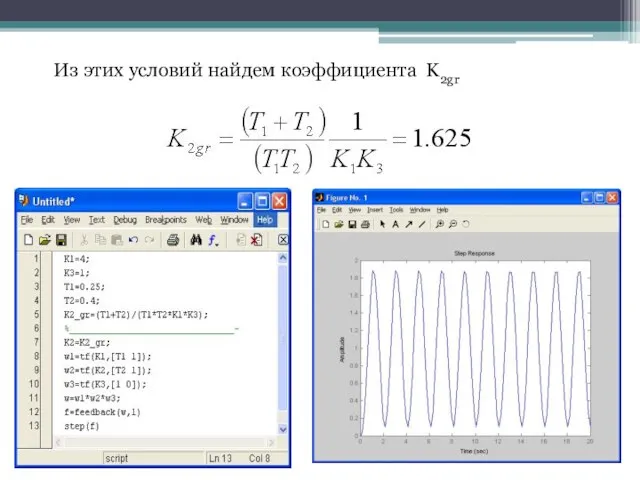
- 26. Из этих условий найдем коэффициента K2gr
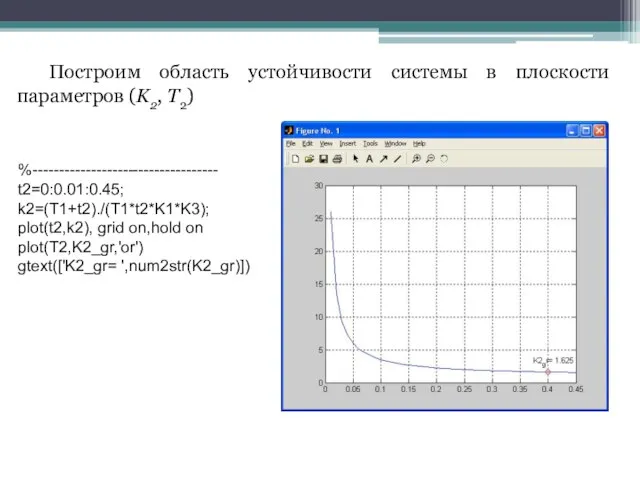
- 27. Построим область устойчивости системы в плоскости параметров (K2, T2) %----------------------------------- t2=0:0.01:0.45; k2=(T1+t2)./(T1*t2*K1*K3); plot(t2,k2), grid on,hold on
- 29. 3) Критерий устойчивости Михайлова Рассмотрим характеристическое уравнение : (13) (14) а мнимая – нечетные степени частоты
- 30. 3) Критерий устойчивости Михайлова Если заданы все коэффициенты и определенное значение частоты ω, то величина D(jω)
- 31. 3) Критерий устойчивости Михайлова Формулировка критерия Михайлова. Автоматическая система управления, описываемая уравнениями п-го порядка будет устойчивой,
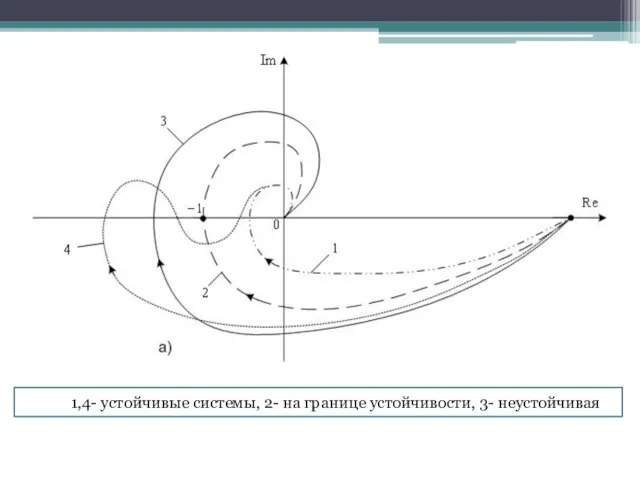
- 32. 3) Критерий устойчивости Михайлова Характеристические кривые, соответствующие устойчивым системам (рисунок б), имеют плавную спиралеобразную форму и
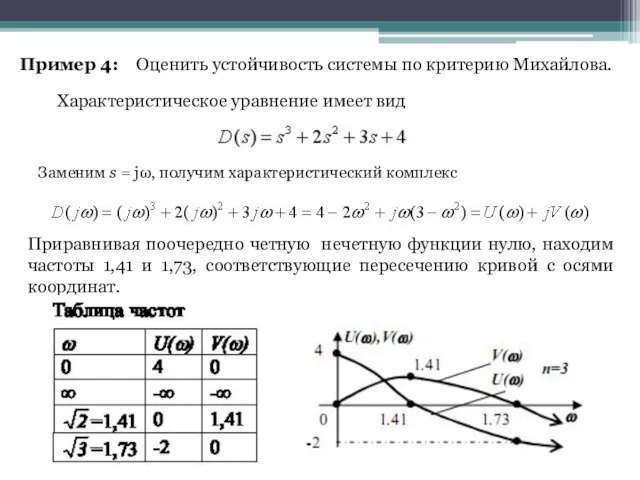
- 33. Пример 4: Оценить устойчивость системы по критерию Михайлова. Заменим s = jω, получим характеристический комплекс Приравнивая
- 34. 3) Критерий устойчивости Михайлова Пример 5: Найти критическое значение коэффициента усиления системы по критерию Михайлова. Характеристическое
- 35. Определяем частоту Частота, соответствующая колебательной границе устойчивости Подставляем в первое уравнение
- 36. 4) Критерий устойчивости Найквиста Критерий устойчивости Найквиста — это также частотный критерий, предложенный в 1932 г.
- 37. 1,4- устойчивые системы, 2- на границе устойчивости, 3- неустойчивая
- 38. 4) Критерий устойчивости Найквиста В случае астатической системы формулировка критерия Найквиста сохраняется, однако при этом возникает
- 40. 5) Определение устойчивости по логарифмическим характеристикам Для нормального функционирования система управления должна обладать и некоторыми запасами
- 41. 5) Определение устойчивости по логарифмическим характеристикам Запас устойчивости по фазe -значение фазы при -частота среза Запас
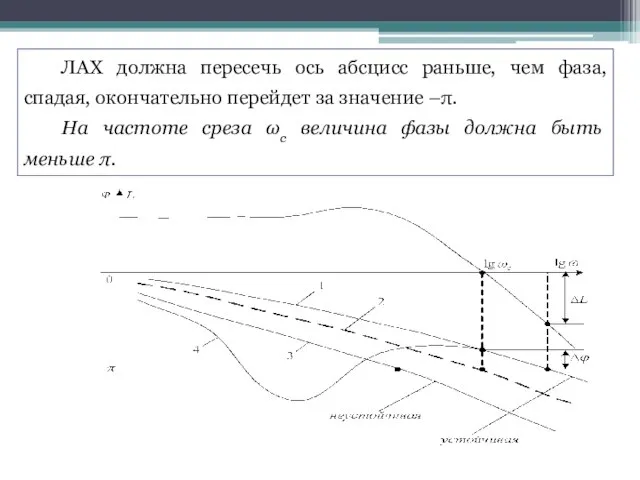
- 42. ЛАХ должна пересечь ось абсцисс раньше, чем фаза, спадая, окончательно перейдет за значение –π. На частоте
- 43. 5) Определение устойчивости по логарифмическим характеристикам Для систем, неустойчивых в разомкнутом состоянии, требования к ЛАХ и
- 44. Запас устойчивости по фазе определяется величиной Δφ, на которую должно возрасти запаздывание по фазе в системе
- 45. Приведем формулы, с помощью которых можно по известным исходным данным рассчитать запасы устойчивости, оценить влияние параметров
- 46. 5) Определение устойчивости по логарифмическим характеристикам Расчетные формулы для системы с астатизмом второго порядка и передаточной
- 47. 5) Определение устойчивости по логарифмическим характеристикам Расчетные формулы для системы с астатизмом второго порядка и передаточной
- 48. 5) Определение устойчивости по логарифмическим характеристикам Расчетные формулы для системы с астатизмом первого порядка и передаточной
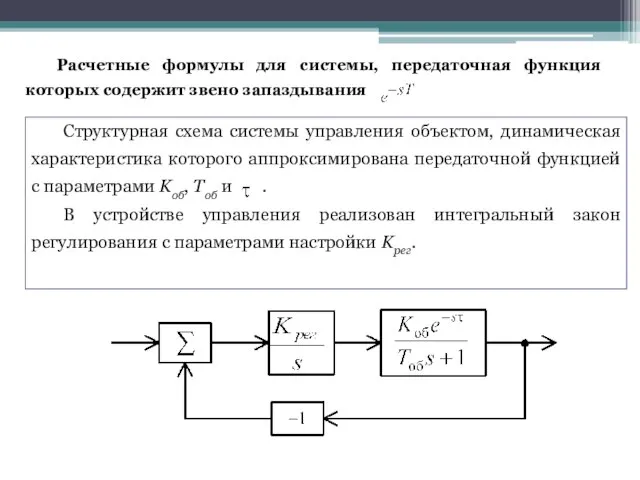
- 49. Расчетные формулы для системы, передаточная функция которых содержит звено запаздывания Структурная схема системы управления объектом, динамическая
- 50. 5) Определение устойчивости по логарифмическим характеристикам Передаточная функция разомкнутой системы: частотная амплитудная характеристика: частотная фазовая характеристика:
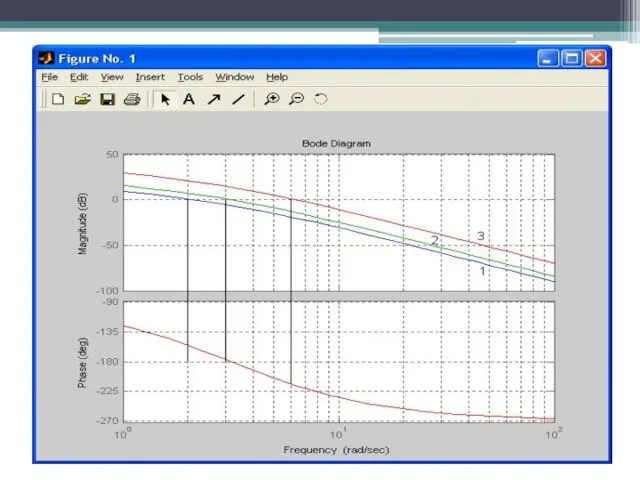
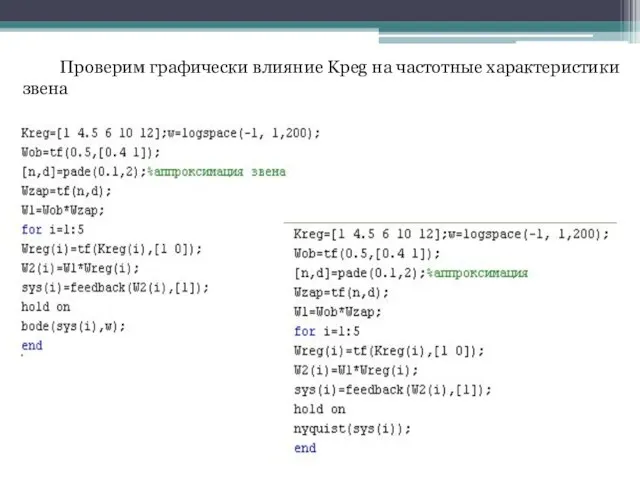
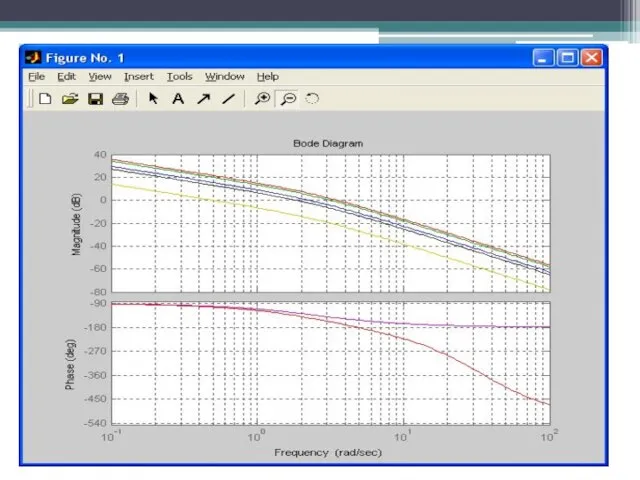
- 51. Проверим графически влияние Kpeg на частотные характеристики звена
- 54. Скачать презентацию




































 День Российского флага
День Российского флага Основы проектирования робототехнических систем. Механизмы управления АПИ. Структура механизмов перевода УБВ в боевое положение
Основы проектирования робототехнических систем. Механизмы управления АПИ. Структура механизмов перевода УБВ в боевое положение сайт Атанель
сайт Атанель Проектирование электроснабжения химического комбината
Проектирование электроснабжения химического комбината (3)
(3) 20170826_za_7_pechatyami._bunin
20170826_za_7_pechatyami._bunin Трудовые ресурсы РФ
Трудовые ресурсы РФ Проект по благоустройству участка детского сада
Проект по благоустройству участка детского сада Клип группы Звёздочки (детский сад)
Клип группы Звёздочки (детский сад) Сертификат PowerPointBase.com
Сертификат PowerPointBase.com Ясака дзиндзя. Синтоизм
Ясака дзиндзя. Синтоизм К стартовому совещанию по договору №473–ЮР/2019 от 16.08.2019 г. на выполнение сейсморазведочных работ
К стартовому совещанию по договору №473–ЮР/2019 от 16.08.2019 г. на выполнение сейсморазведочных работ Государственный социально-гуманитарный университет
Государственный социально-гуманитарный университет
 Герметизация ввода кабеля в устройства СЦБ
Герметизация ввода кабеля в устройства СЦБ 20160412_otkrytyy_urok
20160412_otkrytyy_urok Отчет по программе Воспитания Группа Колокольчик
Отчет по программе Воспитания Группа Колокольчик Конкурс наставничества Сидорова
Конкурс наставничества Сидорова Презентация педагога дополнительного образования Ерохина А.С
Презентация педагога дополнительного образования Ерохина А.С Обереги и талисманы, виды оберегов. Изготовление оберега-лопатки Всех Благ
Обереги и талисманы, виды оберегов. Изготовление оберега-лопатки Всех Благ Памятки в помощь лицам прибывающим из Украины
Памятки в помощь лицам прибывающим из Украины имай насыри - наш земляк
имай насыри - наш земляк Разработка электронной системы управления электрооборудованием трактора беларусь 35 23
Разработка электронной системы управления электрооборудованием трактора беларусь 35 23 Система авто-полива сада
Система авто-полива сада Природные режимы залежей нефти
Природные режимы залежей нефти Чем заняться дома с дошкольником
Чем заняться дома с дошкольником Теория информационного общества
Теория информационного общества Тест про Evoland 1,2
Тест про Evoland 1,2