Содержание
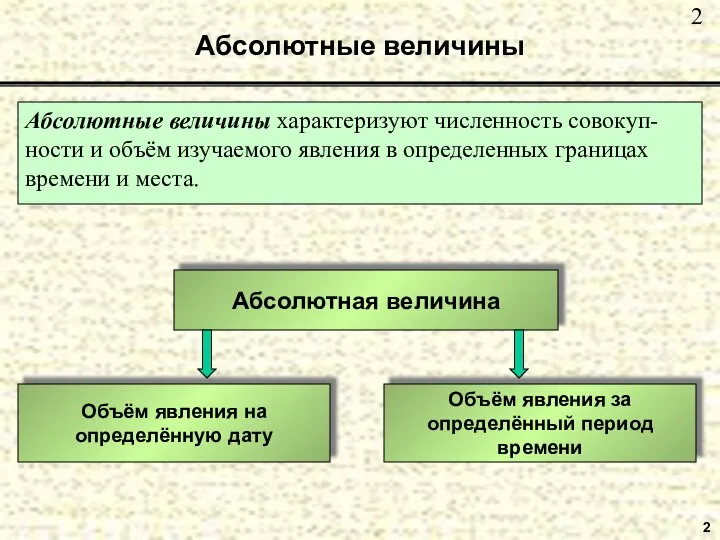
- 2. Абсолютные величины Абсолютные величины характеризуют численность совокуп- ности и объём изучаемого явления в определенных границах времени
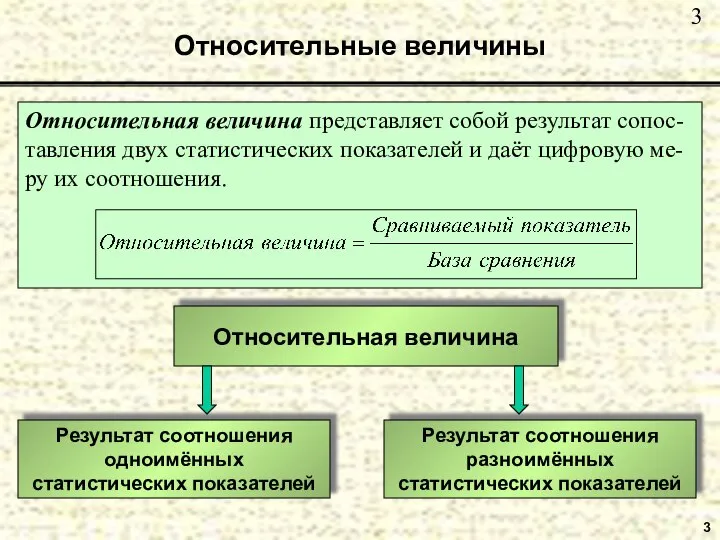
- 3. Относительные величины Относительная величина представляет собой результат сопос-тавления двух статистических показателей и даёт цифровую ме-ру их
- 4. Относительные величины одноимённых статистических показателей в экономике 4 1. Относительные величины динамики характеризует измене-ние явления во
- 5. Относительные величины одноимённых статистических показателей в экономике 5 Пример. Имеются следующие данные о стоимости основного капитала
- 6. Относительные величины одноимённых статистических показателей в экономике 6
- 7. Относительные величины одноимённых статистических показателей в экономике 7
- 8. Относительные величины разноимённых статистических показателей в экономике 8 Эта группа статистических показателей носит название отно-сительных величин
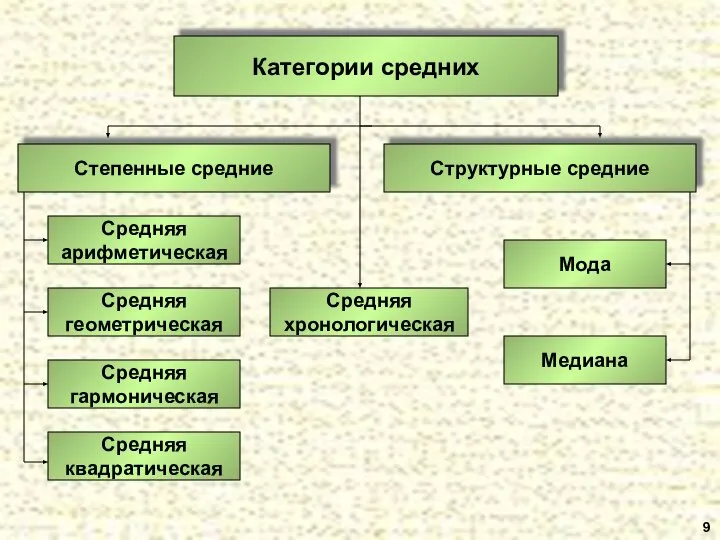
- 9. 9
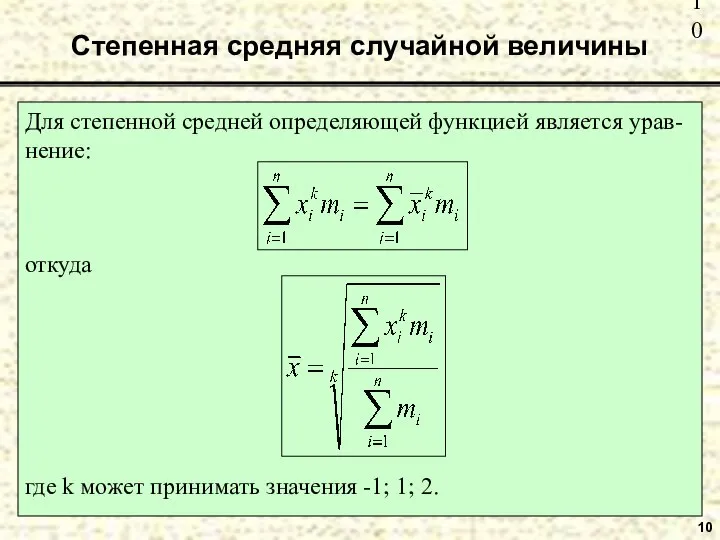
- 10. Степенная средняя случайной величины 10
- 11. Среднее арифметическое значение случайной величины (k=1) Средним арифметичским значением дискретной случайной ве- личины называют сумму произведений
- 12. Среднее арифметическое значение случайной величины (k=1) 12
- 13. Среднее значение суммы случайных величин Среднее значение суммы случайных величин равно сумме средних значений случайных величин.
- 14. Среднее значение произведения случайных величин Среднее значение произведения взаимно независимых случай- ных величин равно произведению средних
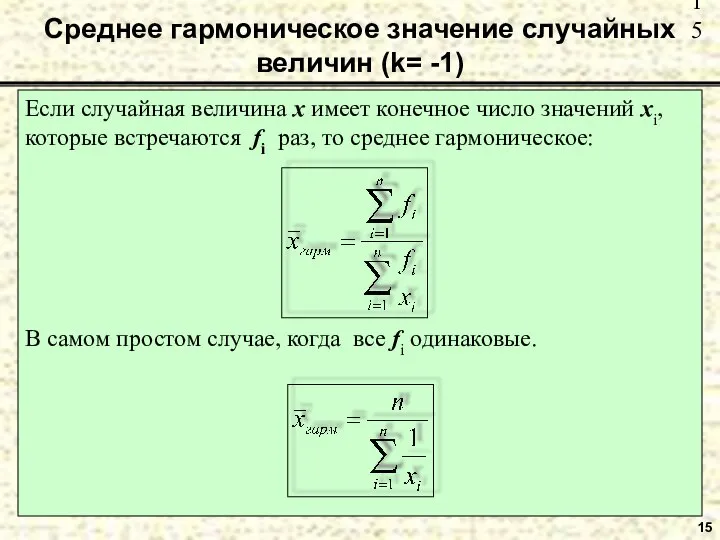
- 15. Среднее гармоническое значение случайных величин (k= -1) Если случайная величина x имеет конечное число значений xi,
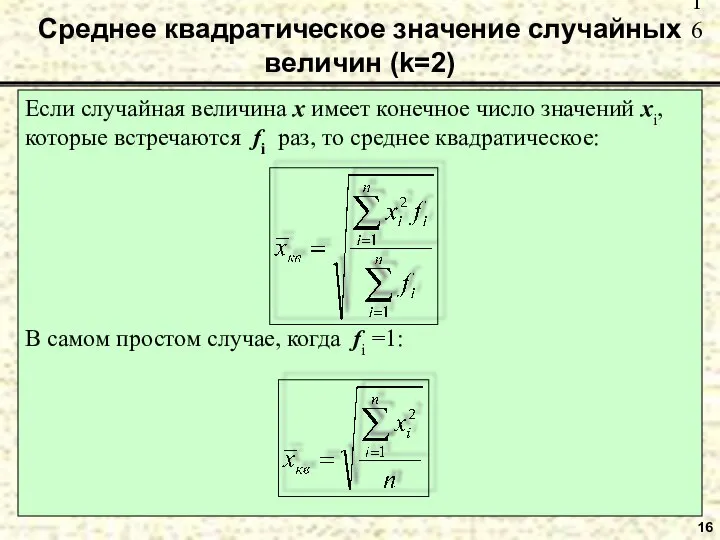
- 16. Среднее квадратическое значение случайных величин (k=2) Если случайная величина x имеет конечное число значений xi, которые
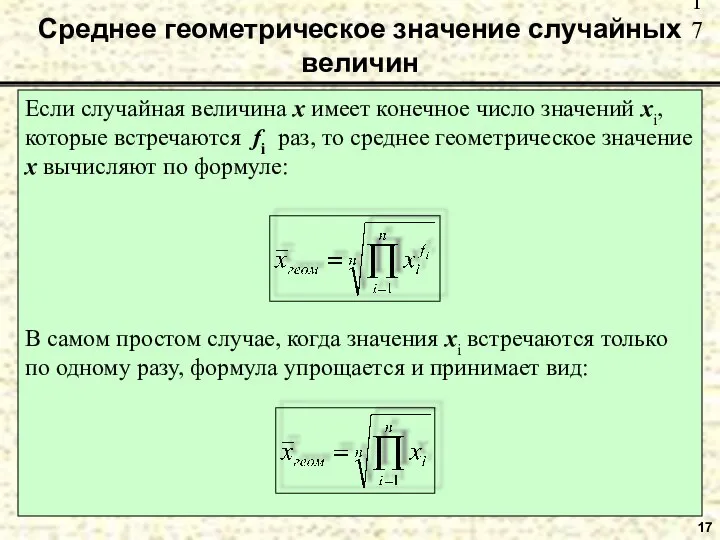
- 17. Среднее геометрическое значение случайных величин Если случайная величина x имеет конечное число значений xi, которые встречаются
- 18. Среднее геометрическое значение случайных величин Пример. Перевозка грузов по автотранспортному предприятию такова: Определить среднемесячный темп роста
- 19. Если случайные величины y1, y2,…, yn представляют собой мо- ментальный динамический ряд, то средний уровень такого
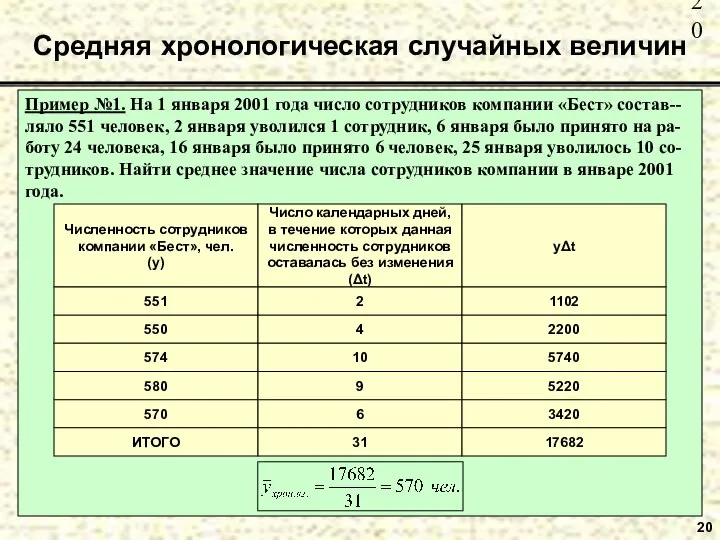
- 20. Пример №1. На 1 января 2001 года число сотрудников компании «Бест» состав--ляло 551 человек, 2 января
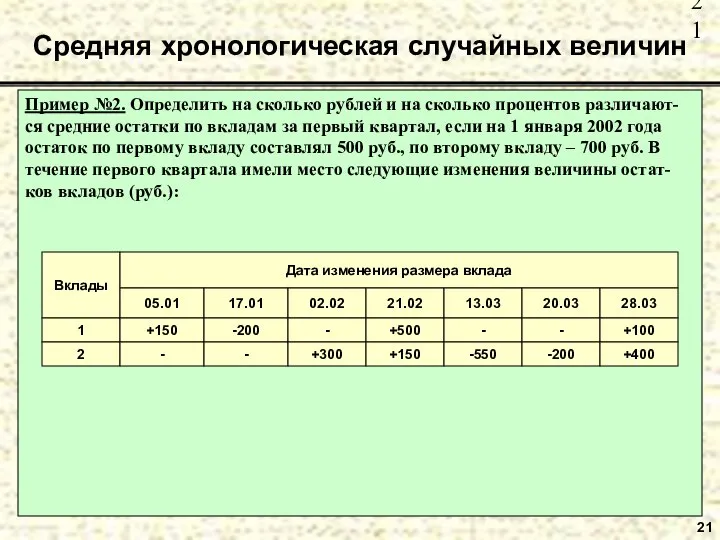
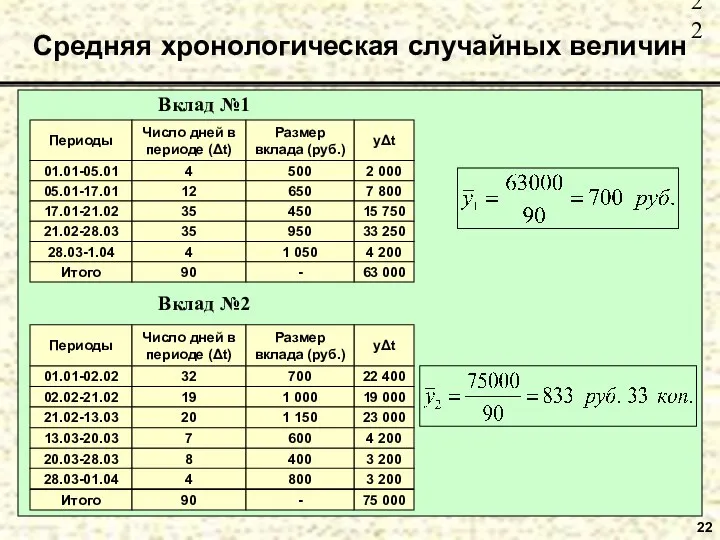
- 21. Пример №2. Определить на сколько рублей и на сколько процентов различают-ся средние остатки по вкладам за
- 22. Средняя хронологическая случайных величин 22
- 23. В случае, если характер изменения уровней ряда в рассматрива-емые периоды неизвестен, и уровни ряда отстоят друг
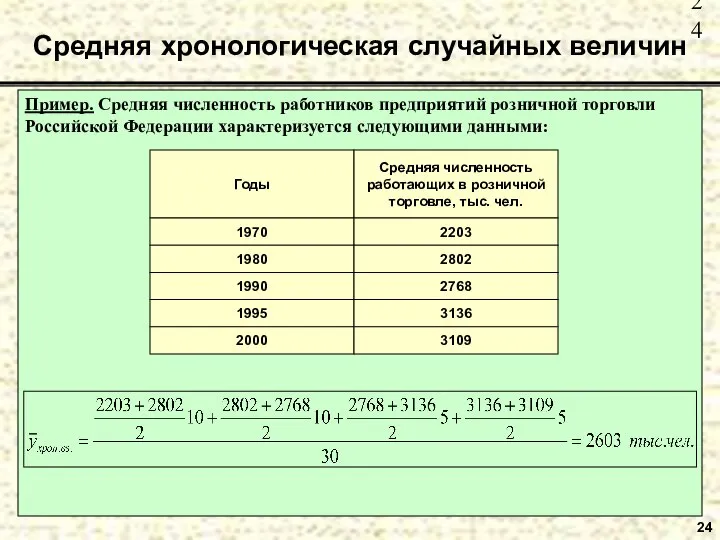
- 24. Пример. Средняя численность работников предприятий розничной торговли Российской Федерации характеризуется следующими данными: Средняя хронологическая случайных величин
- 25. В случае, если промежутки времени между датами, на которые имеются данные одинаковы, и при равномерном изменении
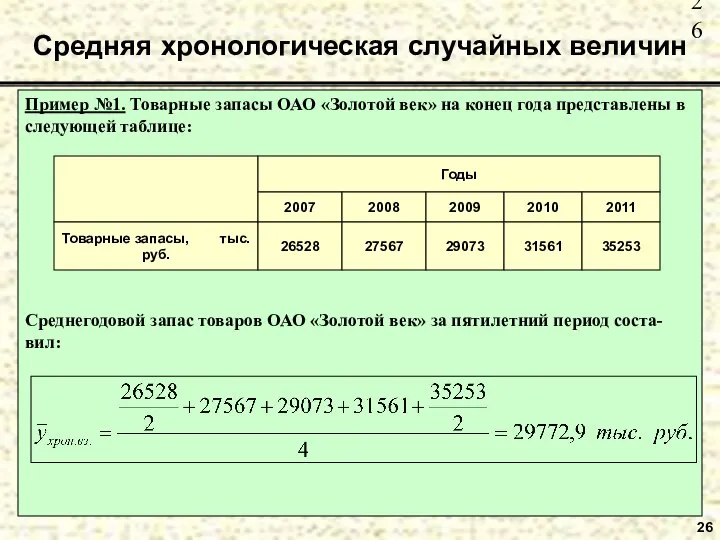
- 26. Пример №1. Товарные запасы ОАО «Золотой век» на конец года представлены в следующей таблице: Среднегодовой запас
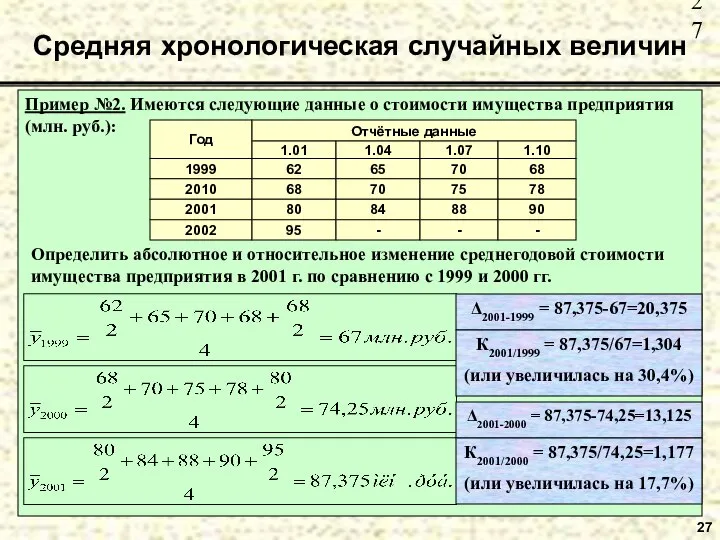
- 27. Пример №2. Имеются следующие данные о стоимости имущества предприятия (млн. руб.): Средняя хронологическая случайных величин 27
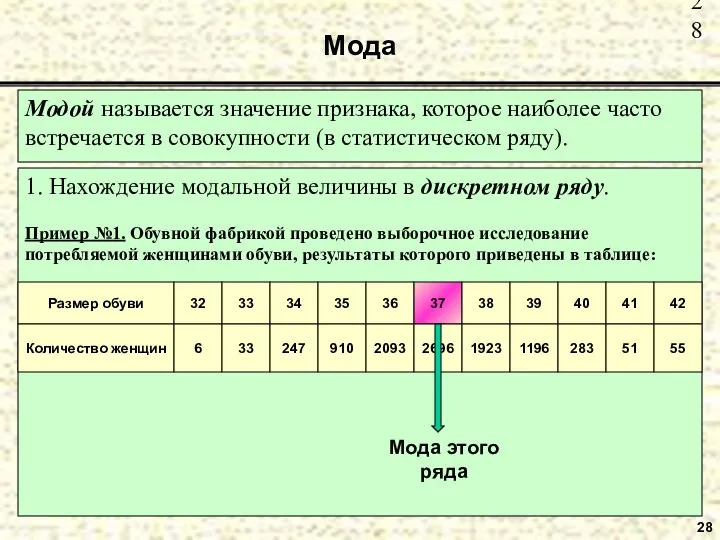
- 28. Модой называется значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду). Мода 28 1.
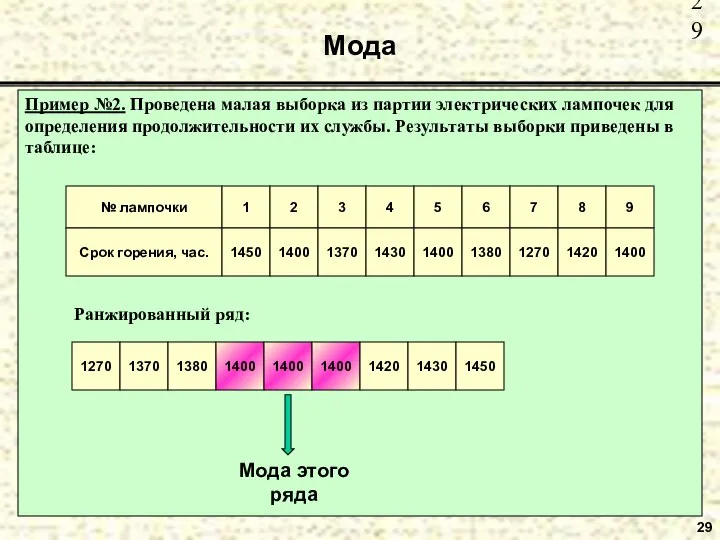
- 29. Мода 29 Пример №2. Проведена малая выборка из партии электрических лампочек для определения продолжительности их службы.
- 30. Мода 30 2. Нахождение модальной величины в интервальном вариаци-онном ряду. где: хmo- нижняя граница модального интервала;
- 31. Мода 31 Пример. В таблице приведены данные о торговой площади магазинов: Необходимо рассчитать моду из интервального
- 32. Медиана 32 Медианой называется серединная варианта упорядоченного вариационного ряда, расположенного в возрастающем или убывающем порядке (ранжированный
- 33. Медиана 33 2. Нахождение медианы интервального ряда. где: xo – нижняя граница медианного интервала; i –
- 34. Медиана 34 Пример. В таблице даны группы семей по среднемесячному доходу на 1 чело-века. Требуется для
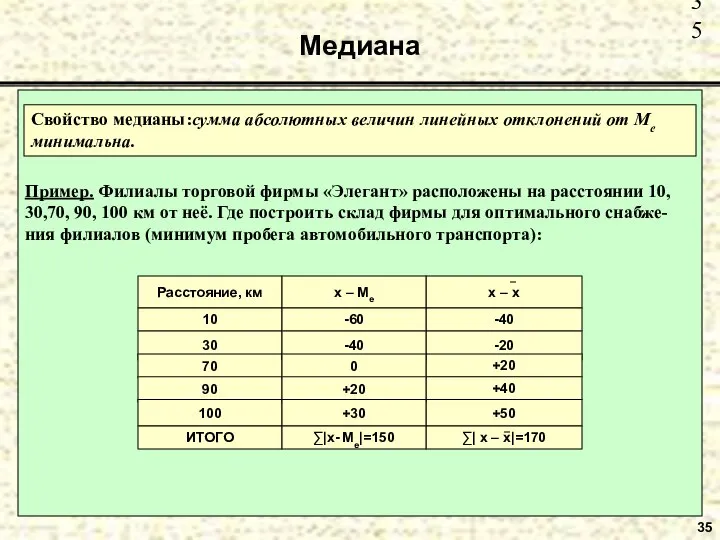
- 35. Медиана 35 Пример. Филиалы торговой фирмы «Элегант» расположены на расстоянии 10, 30,70, 90, 100 км от
- 36. Квартили 36 Более общая постановка вариант, занимающих определённое место в ранжированном ряду, называется порядковой статис-тикой. Квартиль
- 37. Квартили 37 Нижний квартиль: Верхний квартиль: где: xo – нижняя граница квартильных интервалов; i – величи-на
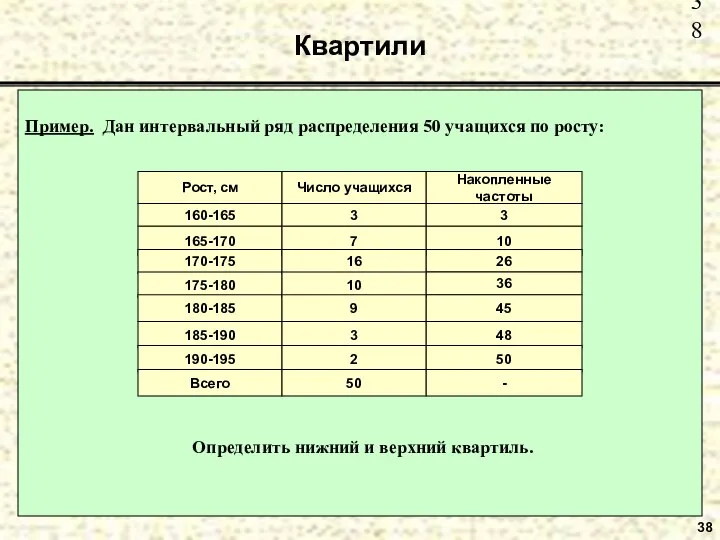
- 38. Квартили 38 Пример. Дан интервальный ряд распределения 50 учащихся по росту: Определить нижний и верхний квартиль.
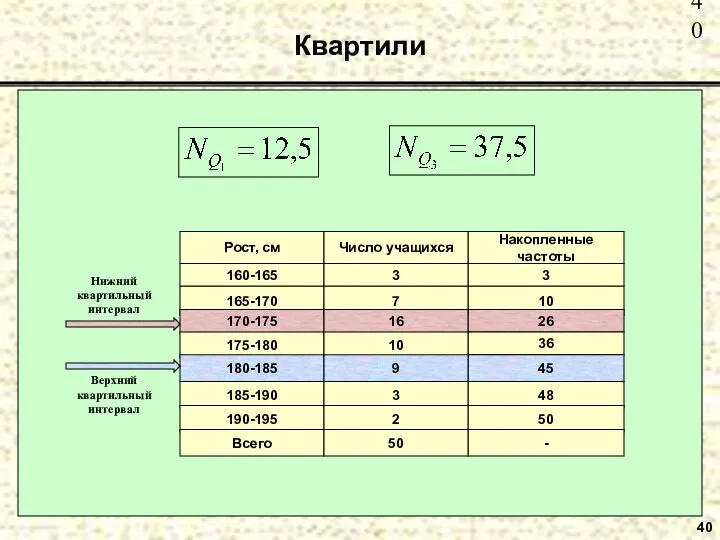
- 39. Квартили 39 Место нижнего квартиля: Место медианы ранжированного интервального ряда: Место верхнего квартиля:
- 40. Квартили 40
- 42. Скачать презентацию





















 Инфекционный мононуклеоз Выполнила: Черепанова Полина студентка 381 «м»
Инфекционный мононуклеоз Выполнила: Черепанова Полина студентка 381 «м» Абстракционизм как особый способ видения мира. Сюрреализм.
Абстракционизм как особый способ видения мира. Сюрреализм. Прокатное производство
Прокатное производство Система Cravath – основа крупного американского юридического бизнеса. Возникновение и развитие
Система Cravath – основа крупного американского юридического бизнеса. Возникновение и развитие Топ 10 ең биік ғимараттар
Топ 10 ең биік ғимараттар Отношение к сметной казни и легализации эвтаназии в РФ
Отношение к сметной казни и легализации эвтаназии в РФ Залог имущества, как способ обеспечения исполнения гражданско-правовых обязательств юридических лиц
Залог имущества, как способ обеспечения исполнения гражданско-правовых обязательств юридических лиц По страницам православной литературы
По страницам православной литературы Презентация История развития федерализма в России
Презентация История развития федерализма в России  Типы данных
Типы данных Красочные аппараты
Красочные аппараты Аттестационная работа. Педагогический колледж – территория здоровья (спортивно-оздоровительный проект)
Аттестационная работа. Педагогический колледж – территория здоровья (спортивно-оздоровительный проект) Презентация Совокупное предложение
Презентация Совокупное предложение Преимущества ручного режима в фотоаппарате
Преимущества ручного режима в фотоаппарате Модульное тестирование на Java
Модульное тестирование на Java Политическая власть
Политическая власть Овощеводство и плодоводство
Овощеводство и плодоводство Кафедра управления и экономики фармации Лекция 1 ВВЕДЕНИЕ В МЕДИЦИНСКУЮ И ФАРМАЦЕВТИЧЕСКУЮ БИОЭТИКУ Доктор фармацевтич
Кафедра управления и экономики фармации Лекция 1 ВВЕДЕНИЕ В МЕДИЦИНСКУЮ И ФАРМАЦЕВТИЧЕСКУЮ БИОЭТИКУ Доктор фармацевтич Конкурентные стратегии компании
Конкурентные стратегии компании  МЕЖДУНАРОДНЫЕ АВИАЦИОННЫЕ ПЕРЕВОЗКИ В УСЛОВИЯХ ГЛОБАЛИЗАЦИИ НА РЫНКЕ ЕС И ВОСТОЧНОЙ ЕВРОПЫ Final thesis
МЕЖДУНАРОДНЫЕ АВИАЦИОННЫЕ ПЕРЕВОЗКИ В УСЛОВИЯХ ГЛОБАЛИЗАЦИИ НА РЫНКЕ ЕС И ВОСТОЧНОЙ ЕВРОПЫ Final thesis  Политические режимы. Недемократические и гибридные режимы. Демократия: проблема определения, современные механизмы
Политические режимы. Недемократические и гибридные режимы. Демократия: проблема определения, современные механизмы Реконструкция поликлиники ГБУЗ «ООКОД» (в динамике, «вид сверху»)
Реконструкция поликлиники ГБУЗ «ООКОД» (в динамике, «вид сверху») Операционная система
Операционная система ИШЕМИЧЕСКАЯ БОЛЕЗНЬ СЕРДЦА Амлаев К. Р. Главный врач МУЗ «Городской центр медицинской профилактики» города Ставрополя кандидат
ИШЕМИЧЕСКАЯ БОЛЕЗНЬ СЕРДЦА Амлаев К. Р. Главный врач МУЗ «Городской центр медицинской профилактики» города Ставрополя кандидат Вознесение. Святая Троица
Вознесение. Святая Троица Налоговая система РФ
Налоговая система РФ  Культура и духовная жизнь общества
Культура и духовная жизнь общества It школа Samsung. Что лучше знать из си новичкам в java
It школа Samsung. Что лучше знать из си новичкам в java