Содержание
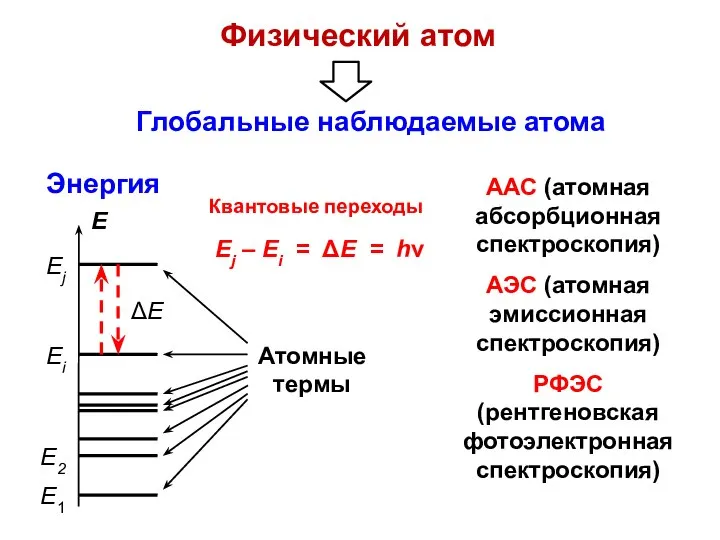
- 2. Физический атом Энергия ААС (атомная абсорбционная спектроскопия) АЭС (атомная эмиссионная спектроскопия) РФЭС (рентгеновская фотоэлектронная спектроскопия)
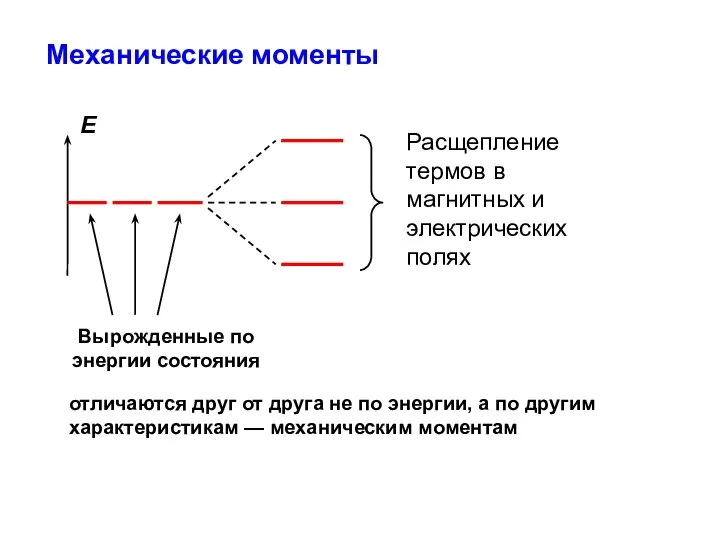
- 3. Механические моменты отличаются друг от друга не по энергии, а по другим характеристикам — механическим моментам
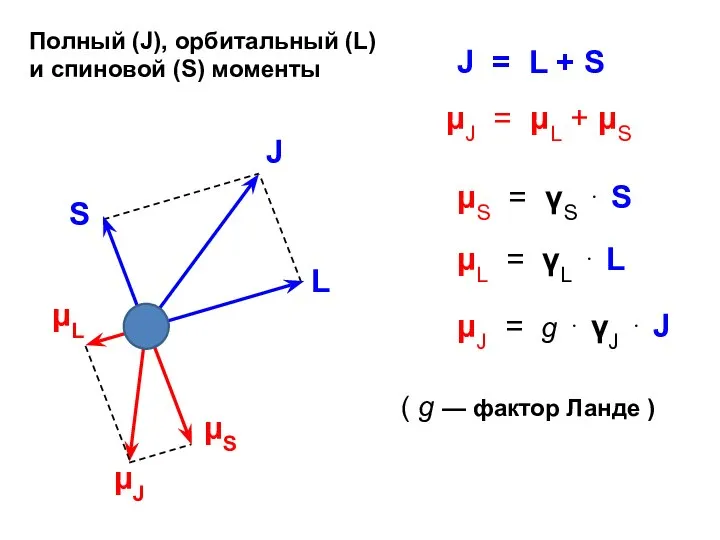
- 4. ( g — фактор Ланде ) Полный (J), орбитальный (L) и спиновой (S) моменты
- 5. Орбитальный механический момент Полный механический момент Спиновой механический момент J, L, S — квантовые числа моментов
- 6. Квантовые числа
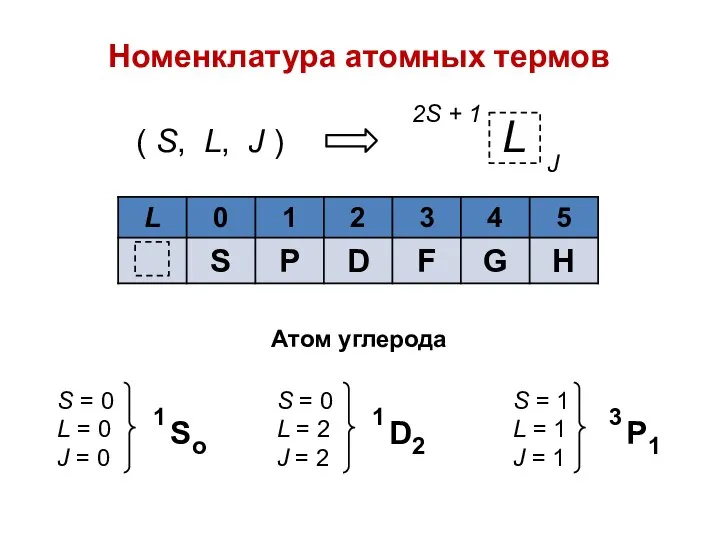
- 7. Номенклатура атомных термов ( S, L, J ) Атом углерода
- 8. Глобальная волновая функция H Φ = E ⋅ Φ Φ(x1, y1, z1, η1, x2, y2, z2,
- 9. Локальная модель атома С ГЛОБАЛЬНОЙ точки зрения любой атом может быть описан стандартным квантово-механическим способом —
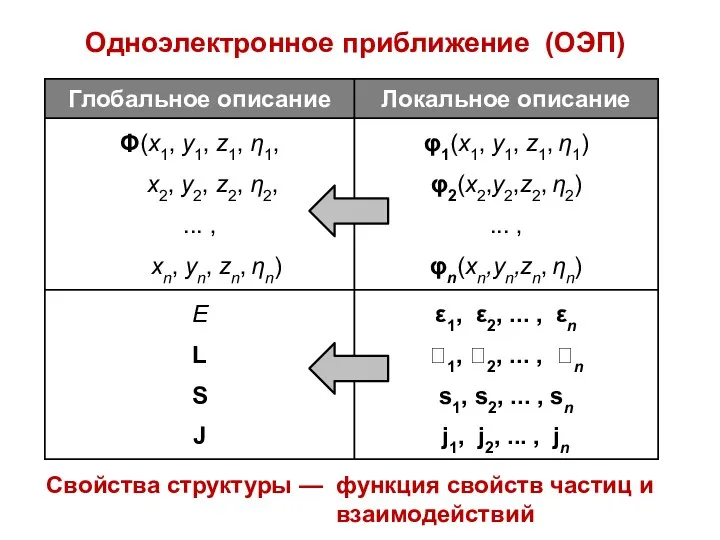
- 10. Одноэлектронное приближение (ОЭП) Свойства структуры — функция свойств частиц и взаимодействий
- 11. Одноэлектронное приближение Каждому электрону приписывается: индивидуальная функция — «атомная орбиталь» (АО) φi (xi, yi, zi, ηi)
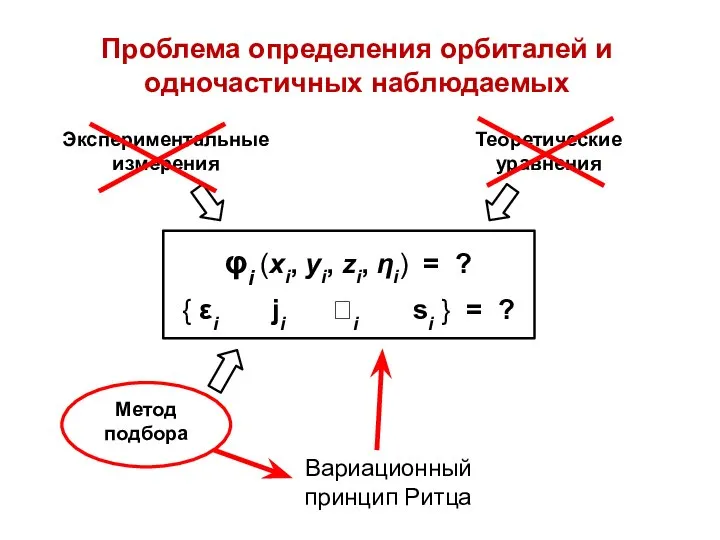
- 12. Проблема определения орбиталей и одночастичных наблюдаемых φi (xi, yi, zi, ηi) = ? { εi ji
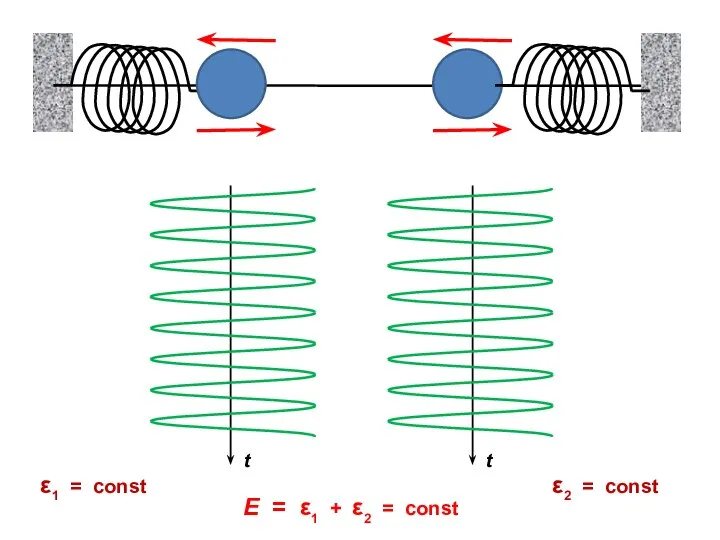
- 13. ε1 = const ε2 = const E = ε1 + ε2 = const
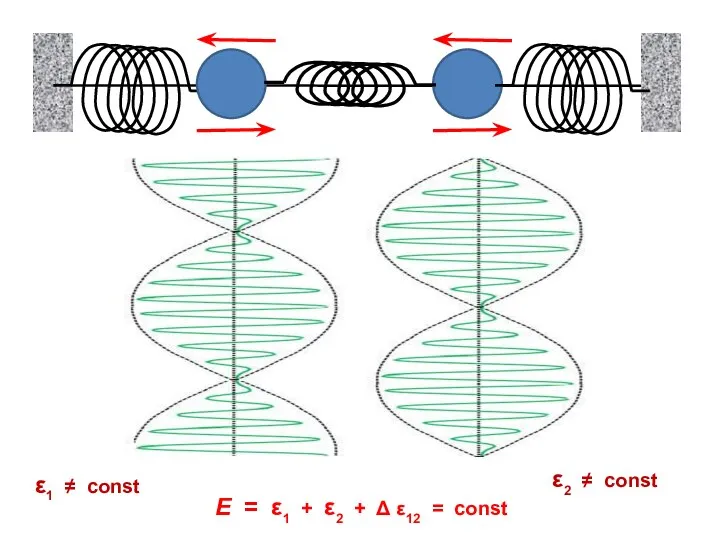
- 14. ε1 ≠ const ε2 ≠ const E = ε1 + ε2 + Δ ε12 = const
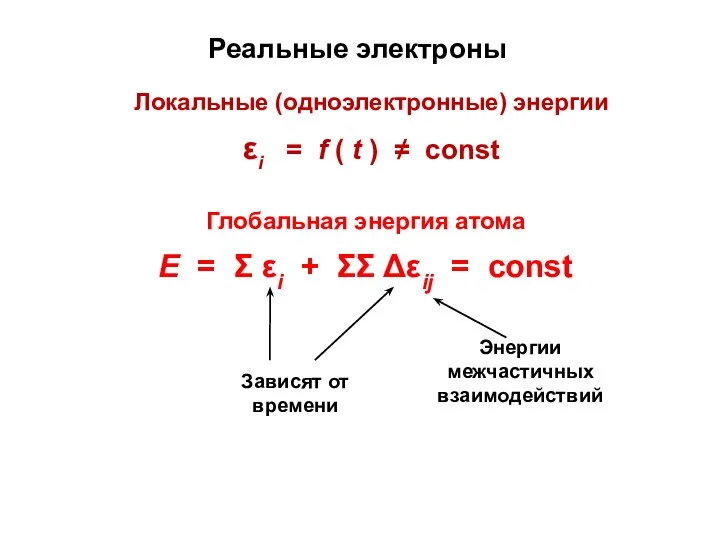
- 15. Реальные электроны Глобальная энергия атома Е = Σ εi + ΣΣ Δεij = const Локальные (одноэлектронные)
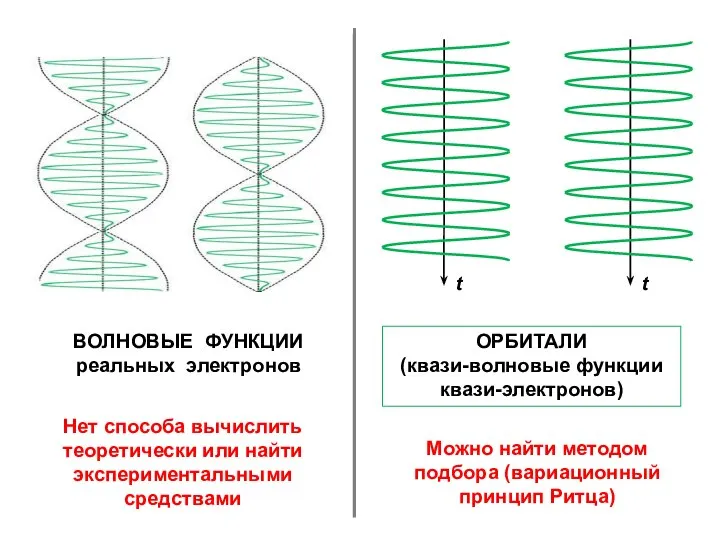
- 16. Квази-электроны (орбитальная модель) Е = Σ ( εi )* + ΔΕ = const ( εi )*
- 17. Нет способа вычислить теоретически или найти экспериментальными средствами Можно найти методом подбора (вариационный принцип Ритца)
- 18. Электроны сами выбирают наиболее простые и экономные способы движения, признаком которых является минимум полной энергии атома:
- 19. Решение первой задачи Н Ф = EФ = E Ф = ?
- 20. Оператор Гамильтона H = T + Uэя + Uээ T = t1 ⊕ t2 ⊕ …
- 21. Пример: атом С (6 электронов) H = t1 + t2 + t3 + t4 + t5
- 22. hi = [(–2/2m)∇2i – Ze2/RiN ] — одноэлектронный гамильтониан Uэфф — «эффективный потенциал», который зависит от
- 23. Уравнения Хартри-Фока (ХФ-уравнения) δЕ = 0 Fi = (hi + Uэфф) — т.н. «оператор Фока» АО
- 24. Система уравнений Хартри-Фока требует особого подхода. Ее можно решить, если известен вид операторов — { hi
- 25. (φ1, φ2, ... , φn)о → (Uэфф)о → уравнения ХФ → → (φ1, φ2, ... ,
- 26. АО являются собственными функциями оператора Фока
- 27. Принципиальное различие: оператор потенциальной энергии в уравнении для атома водорода обладает сферической симметрией, т.е определяется только
- 28. Зависимость Uэфф от углов θ и ϕ не позволяет разделить трехмерную задачу Фока на три одномерные
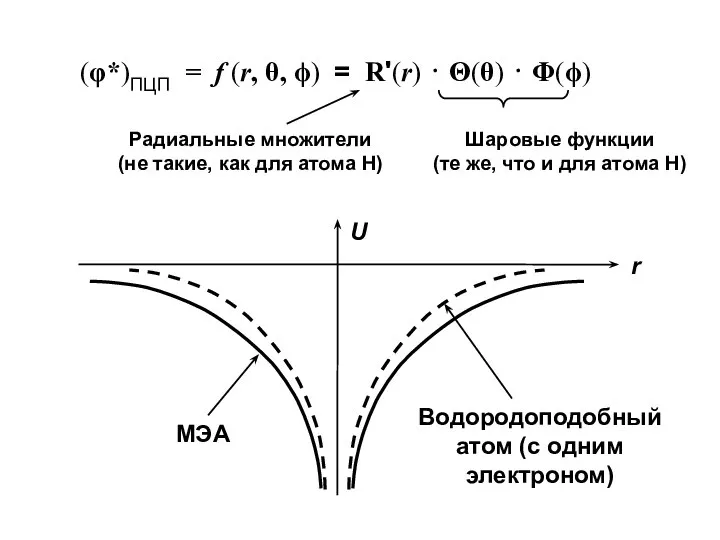
- 29. (φ*)ПЦП = f (r, θ, ϕ) = R'(r) ⋅ Θ(θ) ⋅ Φ(ϕ)
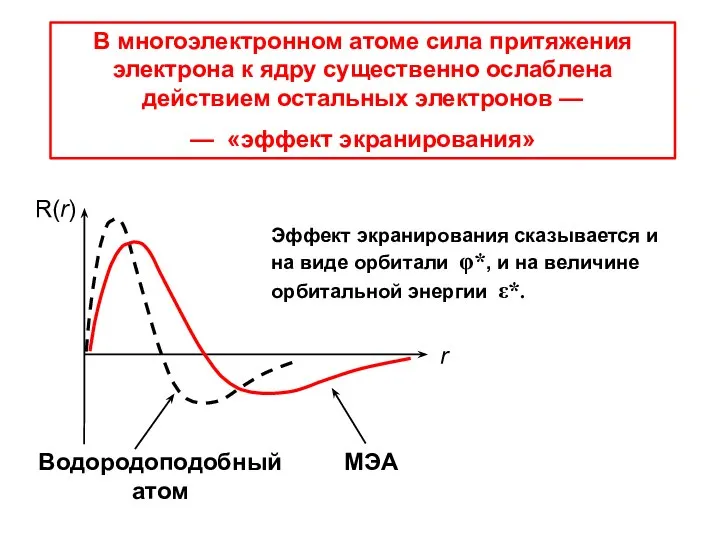
- 30. В многоэлектронном атоме сила притяжения электрона к ядру существенно ослаблена действием остальных электронов — — «эффект
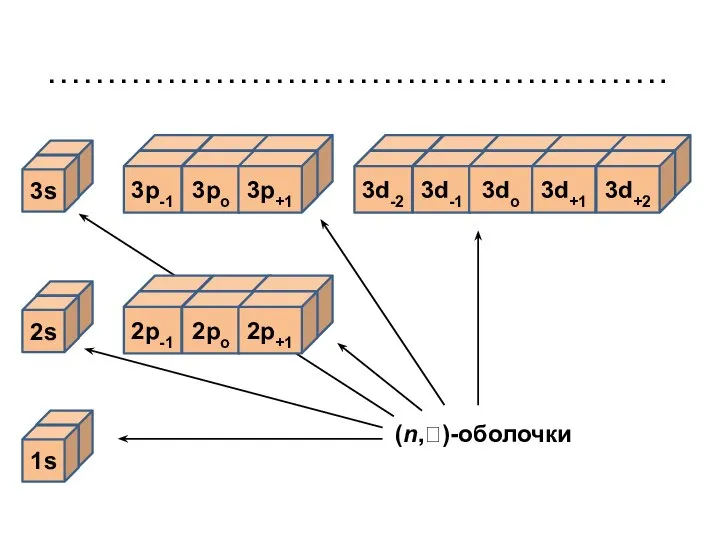
- 31. n — главное квантовое число, нумерующее радиальную функцию, (n – δ) = n* — т.н. «эффективное»
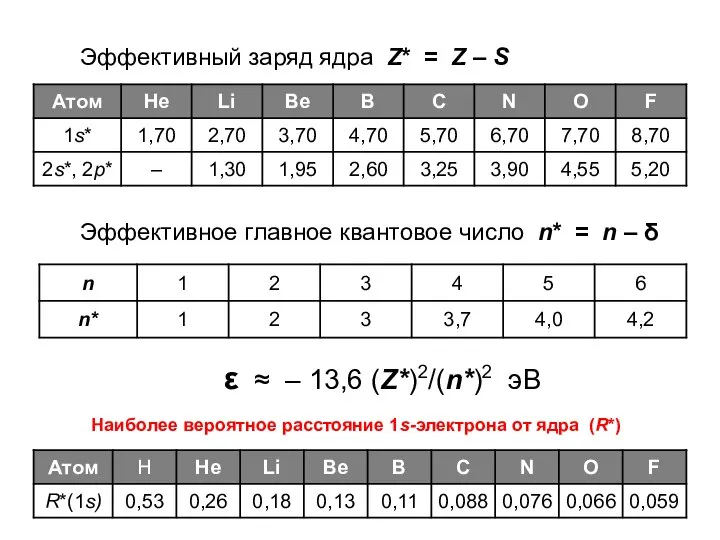
- 32. Эффективный заряд ядра Z* = Z – S Эффективное главное квантовое число n* = n –
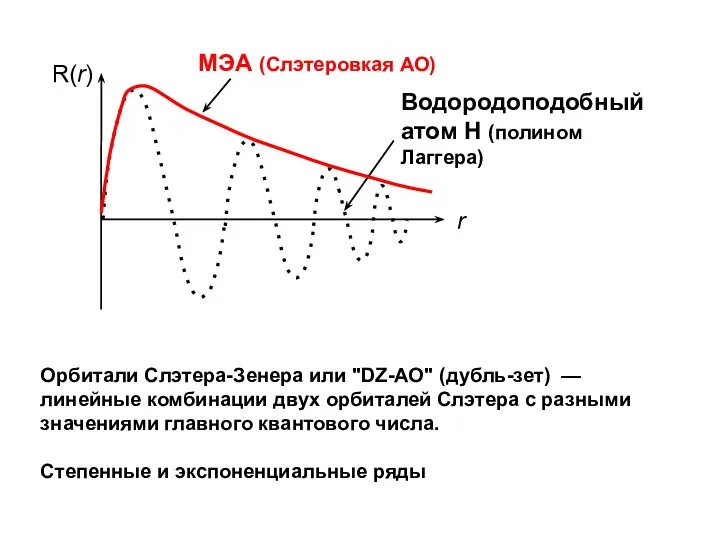
- 33. Орбитали Слэтера-Зенера или "DZ-АО" (дубль-зет) — линейные комбинации двух орбиталей Слэтера с разными значениями главного квантового
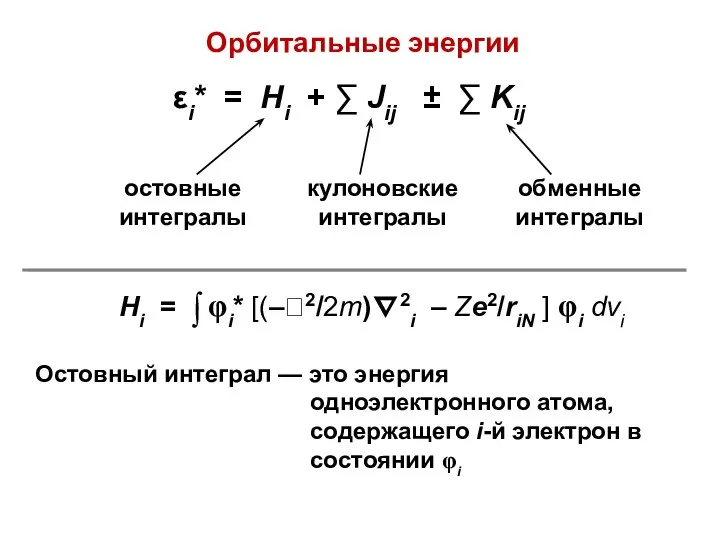
- 34. εi* = Hi + ∑ Jij ± ∑ Kij Орбитальные энергии Остовный интеграл — это энергия
- 36. Полная энергия МЭА
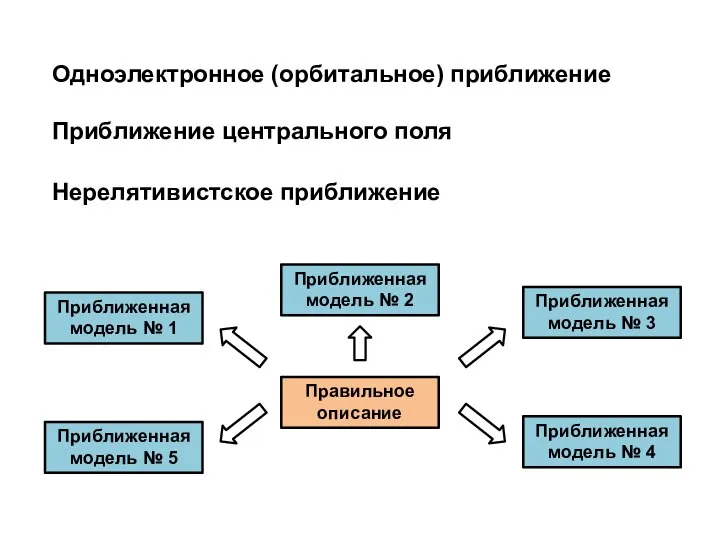
- 37. Оболочечная модель МЭА 1. Одноэлектронное приближение: каждому электрону соответствует индивидуальное состояние. 2. Приближение центрального поля: индивидуальные
- 38. Каждому электрону соответствует стандартный набор наблюдаемых, выражаемых через квантовые числа: Орбитальный механический момент Спиновой механический момент
- 40. Электронная конфигурация — способ распределения электронов по состояниям (1s)ν1 (2s)ν2 (2p)ν3 (3s)ν4 (3p)ν5 (3d)ν6 … Среди
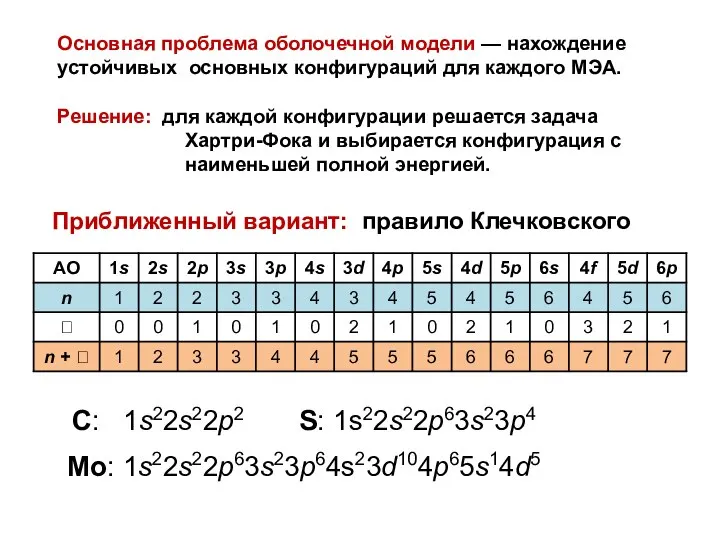
- 41. Основная проблема оболочечной модели — нахождение устойчивых основных конфигураций для каждого МЭА. Решение: для каждой конфигурации
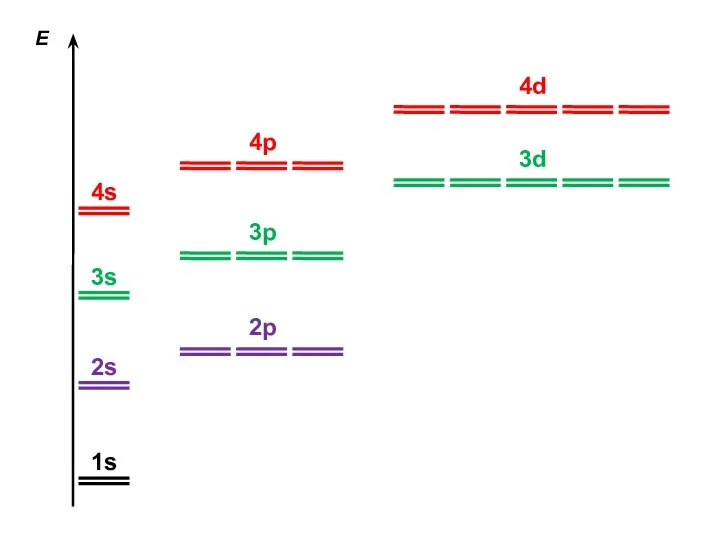
- 42. Е 1s 2s 3s 4s 2p 3p 4p 3d 4d
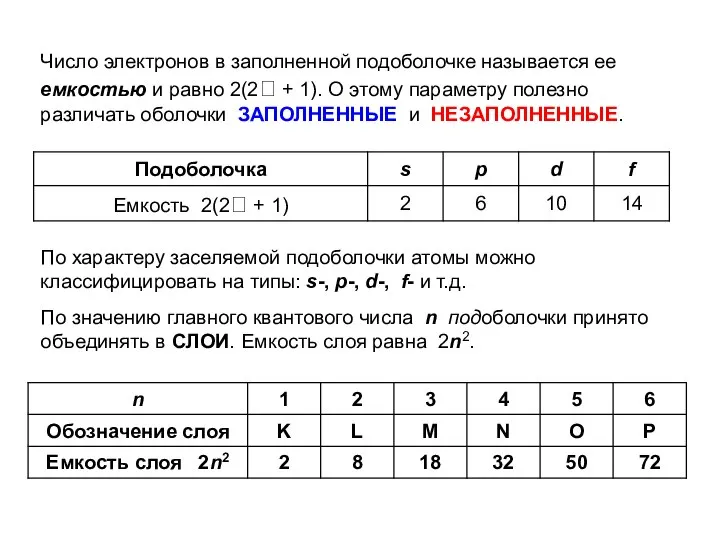
- 43. Число электронов в заполненной подоболочке называется ее емкостью и равно 2(2 + 1). О этому параметру
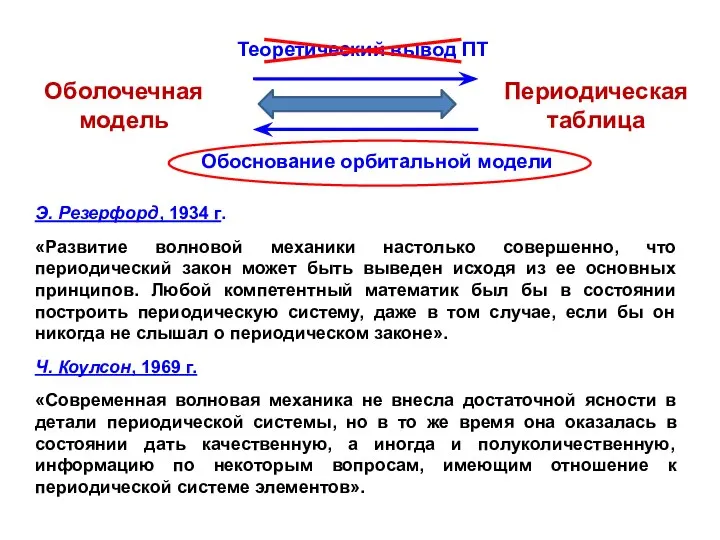
- 45. Э. Резерфорд, 1934 г. «Развитие волновой механики настолько совершенно, что периодический закон может быть выведен исходя
- 46. Одноэлектронное (орбитальное) приближение Нерелятивистское приближение Приближение центрального поля
- 47. Заселение незаполненных оболочек Внутри каждой (n, )-оболочки значения квантовых чисел n и постоянны, и правила
- 48. Поскольку орбитальные энергии всех 2р-АО одинаковы, на полную энергию атома оказывают влияние небольшие вклады, связанные с
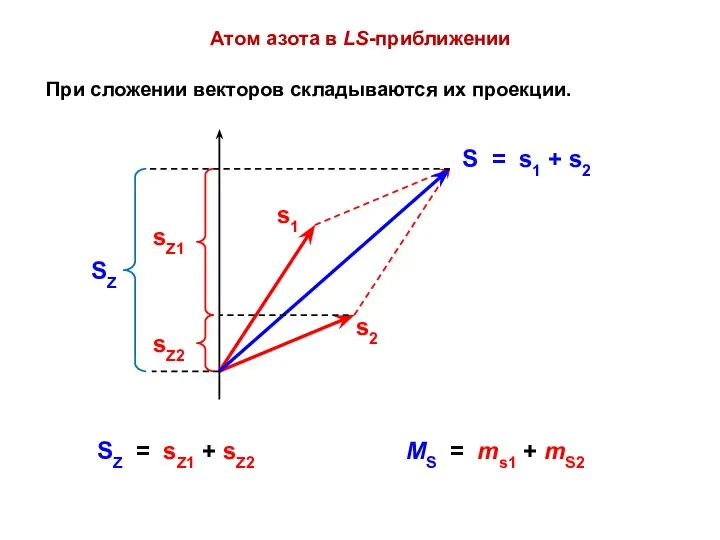
- 49. 1. LS-приближение, справедливое для легких атомов (Z Сложение производится отдельно для орбитальных и отдельно для спиновых
- 50. При сложении векторов складываются их проекции. Атом азота в LS-приближении SZ = sZ1 + sZ2 MS
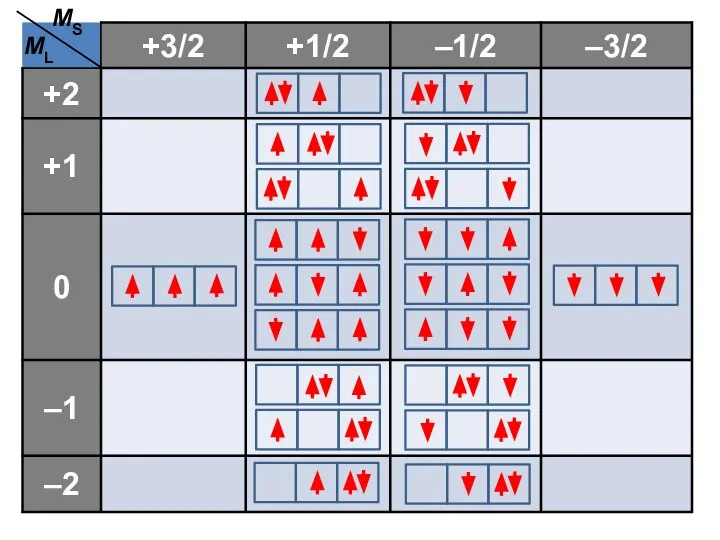
- 51. Длина проекции глобального вектора определяется суммой магнитных чисел локальных векторов: ML = m1 + m2 +
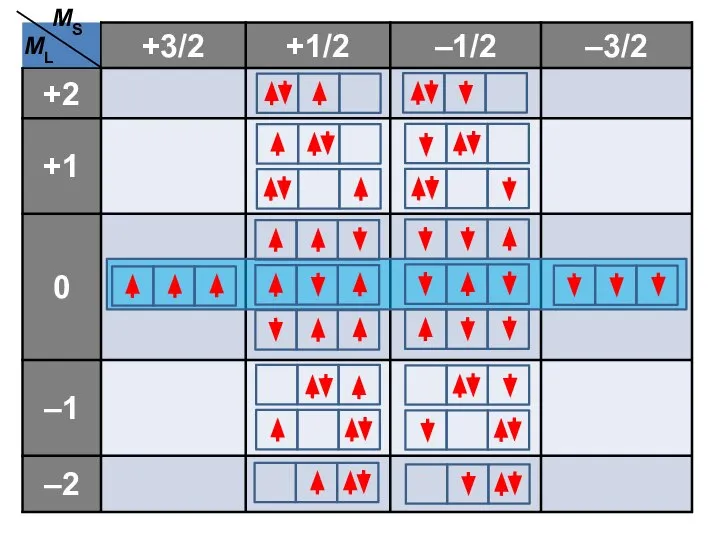
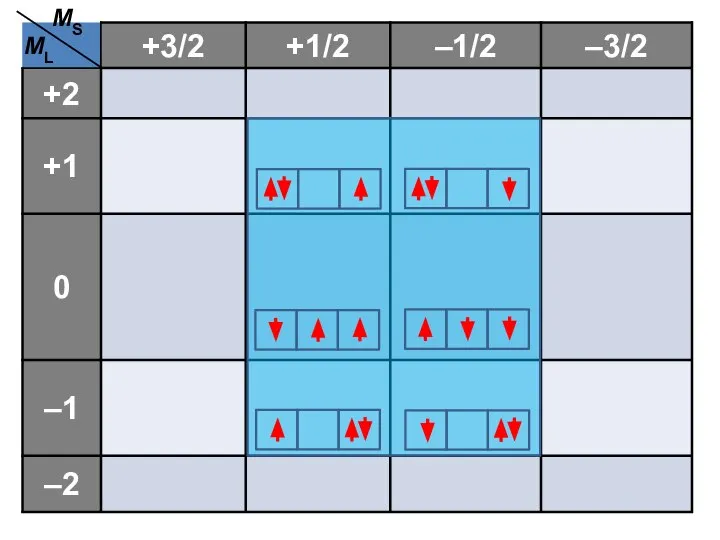
- 52. MS ML
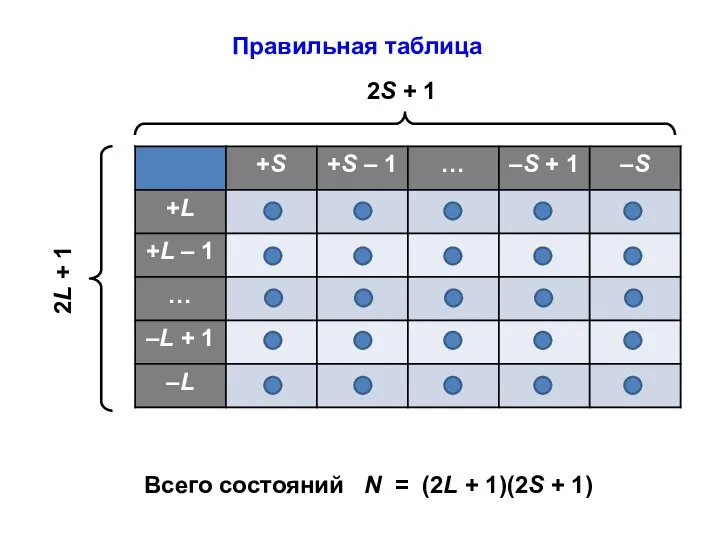
- 53. Правильная таблица Всего состояний N = (2L + 1)(2S + 1)
- 54. MS ML
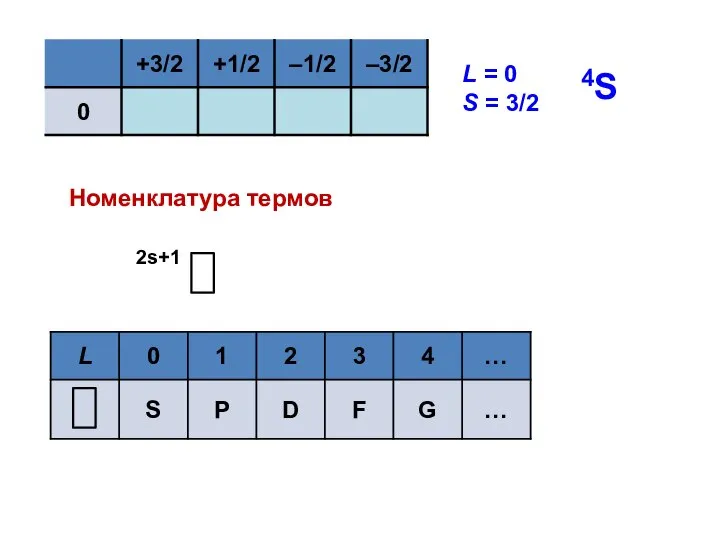
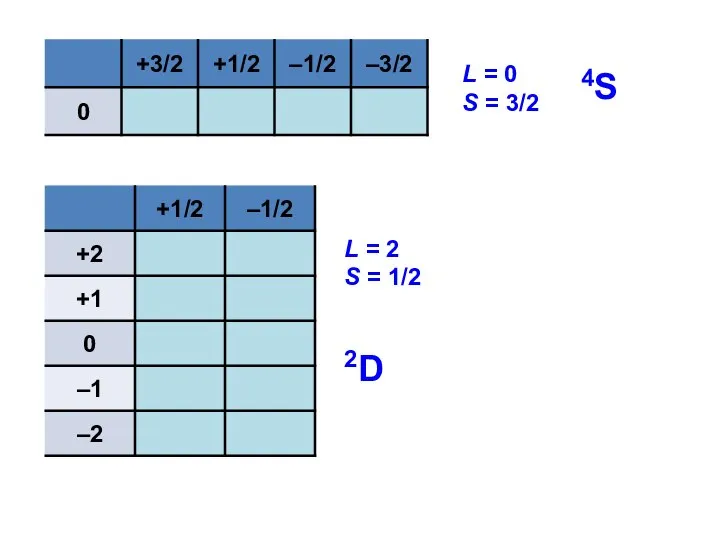
- 55. L = 0 S = 3/2 4S Номенклатура термов
- 56. MS ML
- 57. L = 0 S = 3/2 L = 2 S = 1/2 4S 2D
- 58. MS ML
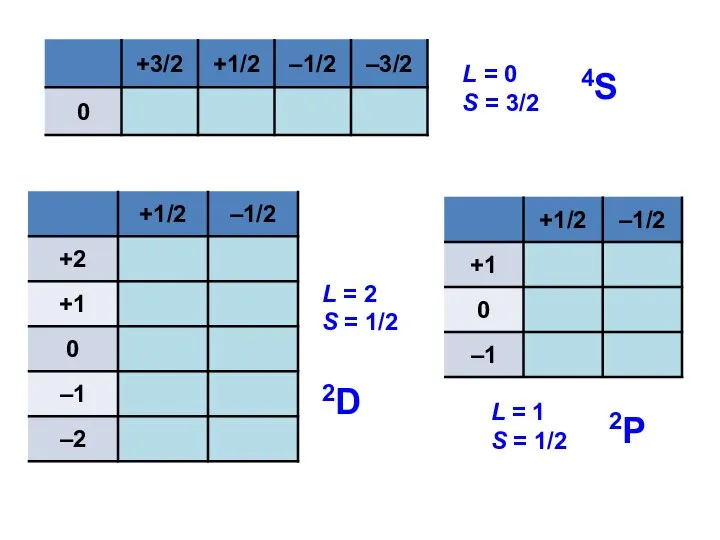
- 59. L = 0 S = 3/2 L = 1 S = 1/2 L = 2 S
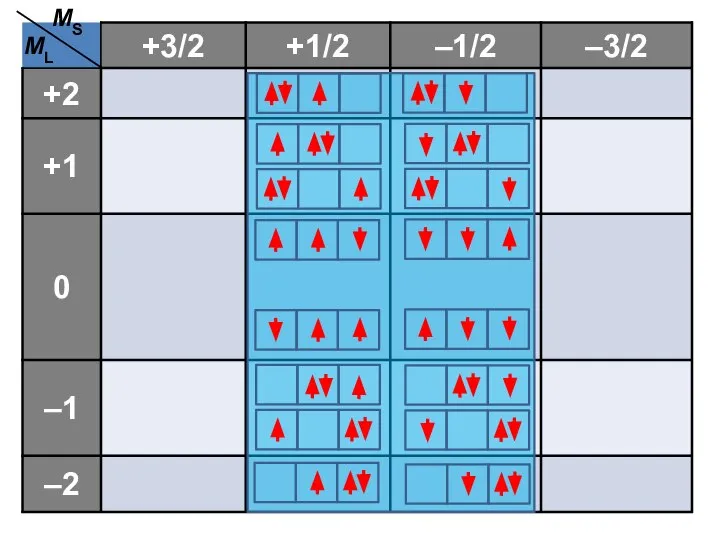
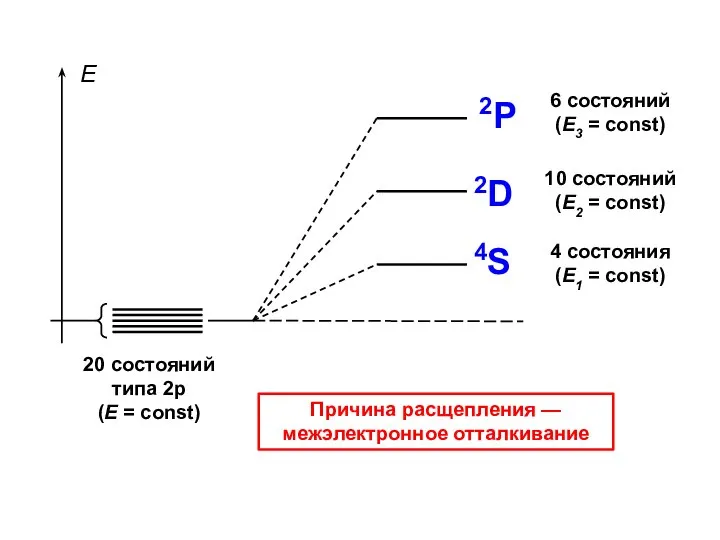
- 60. Зная принадлежность состояний к определенным термам, можно предсказать их распределение по энергетической шкале. Правила Хунда: 1
- 61. Причина расщепления — межэлектронное отталкивание
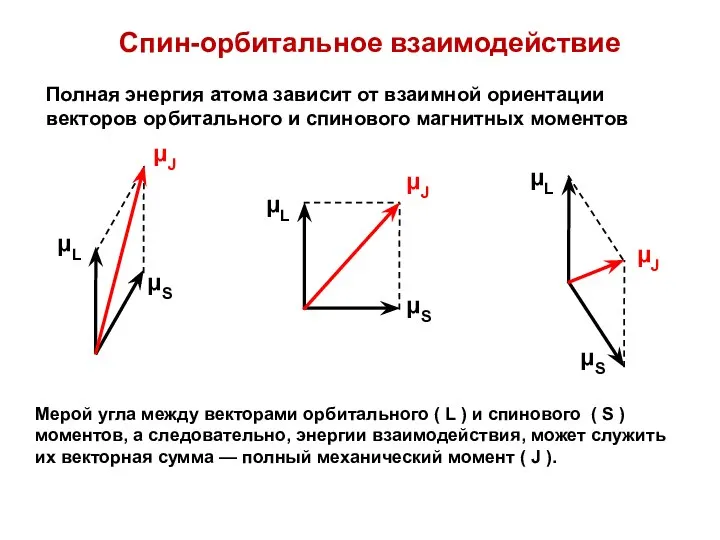
- 62. Спин-орбитальное взаимодействие Полная энергия атома зависит от взаимной ориентации векторов орбитального и спинового магнитных моментов Мерой
- 63. Вычисление величины полного момента | J |2 = 2 [J(J + 1)] J = (L +
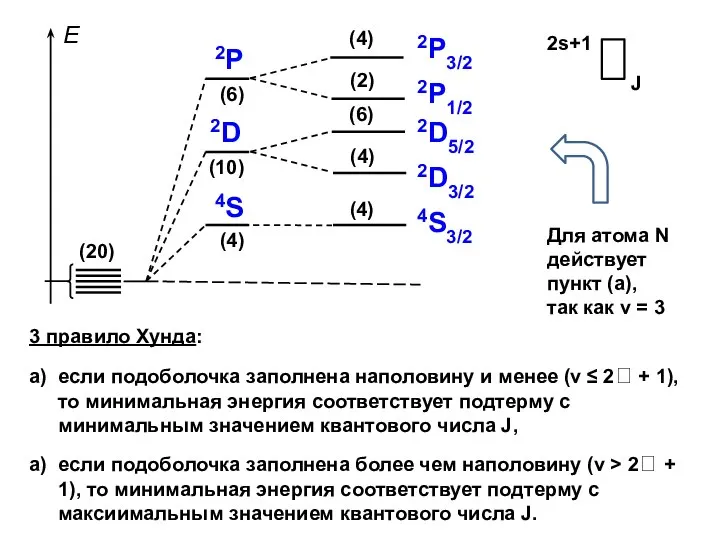
- 64. 3 правило Хунда: а) если подоболочка заполнена наполовину и менее (ν ≤ 2 + 1), то
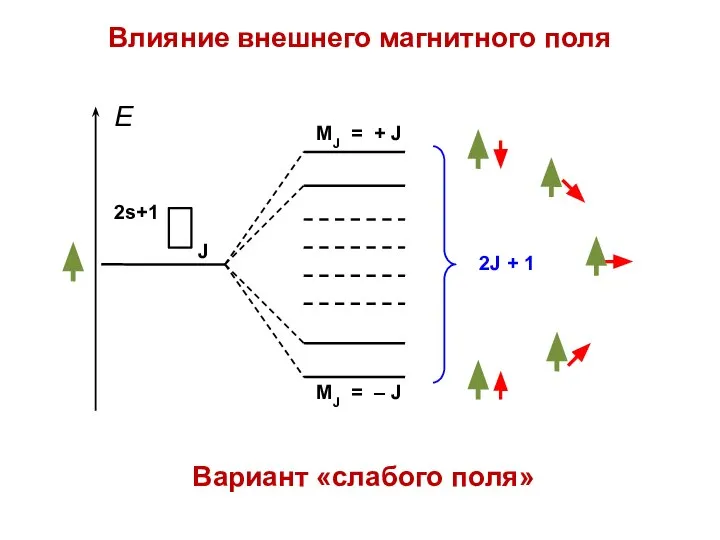
- 65. Влияние внешнего магнитного поля Вариант «слабого поля»
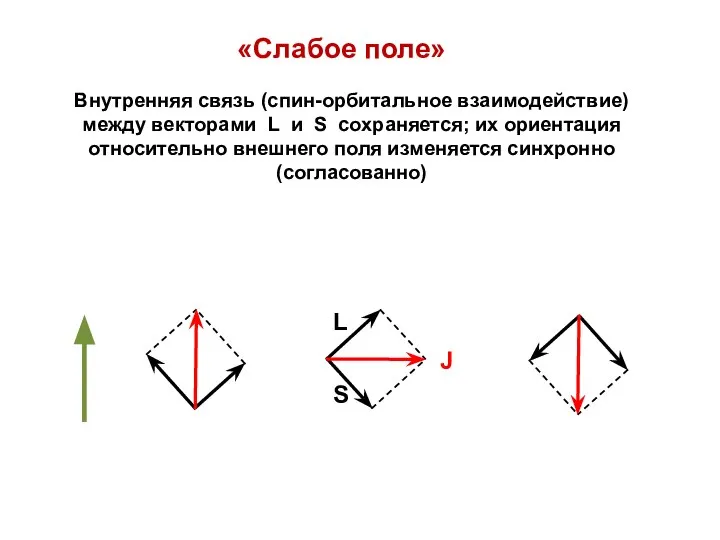
- 66. «Слабое поле» Внутренняя связь (спин-орбитальное взаимодействие) между векторами L и S сохраняется; их ориентация относительно внешнего
- 68. Скачать презентацию










![hi = [(–2/2m)∇2i – Ze2/RiN ] — одноэлектронный гамильтониан Uэфф —](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1308401/slide-21.jpg)


















 Holidey holi
Holidey holi СЕКРЕТЫ ОБЩЕНИЯ
СЕКРЕТЫ ОБЩЕНИЯ Политическая власть
Политическая власть Поступление в БПОУ ВО «Грязовецкий политехнический техникум»
Поступление в БПОУ ВО «Грязовецкий политехнический техникум» Сегментирование рынка М.Видео
Сегментирование рынка М.Видео Позиционирование, Декоративные элементы
Позиционирование, Декоративные элементы Проект организации работ по сооружению железнодорожного земляного полотна
Проект организации работ по сооружению железнодорожного земляного полотна Взаимодействие западноевропейских культур в первой половине XX века
Взаимодействие западноевропейских культур в первой половине XX века CoDeSys CNC functionality
CoDeSys CNC functionality Сервисный тренинг EXD06 Ассистент смены полосы движения (Side Scan Assist)
Сервисный тренинг EXD06 Ассистент смены полосы движения (Side Scan Assist) Как мотивировать и быть мотивированным.
Как мотивировать и быть мотивированным. 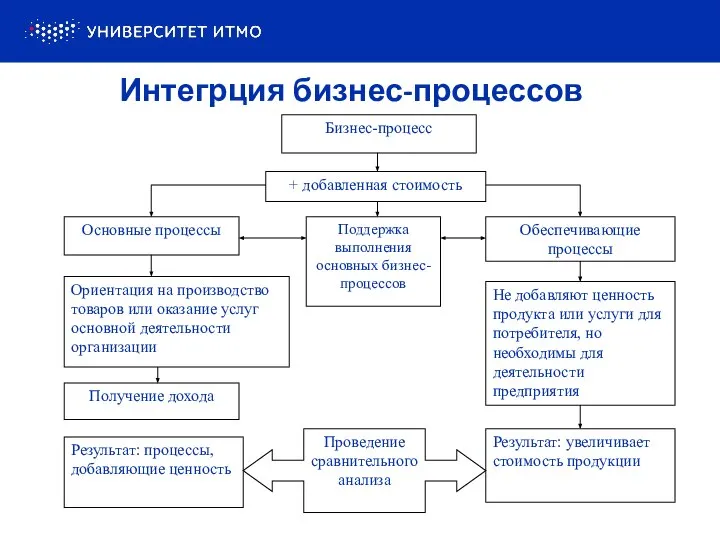 Интеграция бизнес-процессов
Интеграция бизнес-процессов Орта Азия мен Иранның мәдениеті
Орта Азия мен Иранның мәдениеті Билль о правах Презентацию подготовили Студенты группы Ю – 103 Казьмин
Билль о правах Презентацию подготовили Студенты группы Ю – 103 Казьмин  Презентация «ОБЯЗАТЕЛЬСТВА ВСЛЕДСТВИЕ НЕОСНОВАТЕЛЬНОГО ОБОГАЩЕНИЯ»
Презентация «ОБЯЗАТЕЛЬСТВА ВСЛЕДСТВИЕ НЕОСНОВАТЕЛЬНОГО ОБОГАЩЕНИЯ» Ватикан
Ватикан Виды статистического наблюдения по фактору времени
Виды статистического наблюдения по фактору времени Этические принципы и юридическая ответственность психолога
Этические принципы и юридическая ответственность психолога Искусство Франции XVIII века. Живопись
Искусство Франции XVIII века. Живопись Работа гейм-дизайнера
Работа гейм-дизайнера Искусство и его виды. 6 класс
Искусство и его виды. 6 класс Презентация Краткий конспект лекций
Презентация Краткий конспект лекций  Вне церкви нет спасения
Вне церкви нет спасения Определение численности персонала предприятия
Определение численности персонала предприятия Каноническое право
Каноническое право Движение Твердого Тела СО дной Неподвижной Точкой
Движение Твердого Тела СО дной Неподвижной Точкой  Выполнение логических операций
Выполнение логических операций Обязательное социальное медицинское страхование
Обязательное социальное медицинское страхование