Содержание
- 2. Определение нелинейного уравнения В общем виде нелинейное уравнение с одним неизвестным можно записать в виде Y(x)
- 3. а) Алгебраическими называются уравнения Y(x)=0, которые могут быть представлены в форме канонического полинома: Типы нелинейных уравнений:
- 4. Примеры трансцендентных уравнений: Любимов Е.Б.
- 5. Решением или корнем уравнения Y(x)=0 (1) называется значения аргумента х, обращающее равенство (1) в тождество. Любимов
- 6. Методы решения нелинейных уравнений Аналитические (прямые, точные) методы решения: Методы, позволяющие записать решение уравнения в виде
- 7. Аналитические решения могут быть получены для алгебраических уравнений не выше четвертой степени и для некоторых видов
- 8. Алгебраические уравнения, имеющие аналитические решения: линейные уравнения: a*x+b=0 (или a0 + a1*x = 0); квадратные уравнения:
- 9. Итерационные методы – методы последовательных приближений, реализуют алгоритмы, обеспечивающие нахождение решения за несколько последовательно выполняемых шагов
- 10. Общий подход к решению нелинейных уравнений Решение нелинейных уравнений численными методами обычно осуществляется в два этапа:
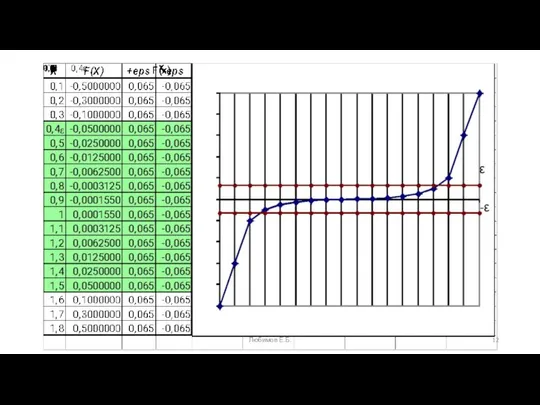
- 11. Признак нахождения корня в интервале [a; b] Y(a)*Y(b) Обычно решение считается найденным, если | Y(xi) |
- 12. ε -ε Любимов Е.Б.
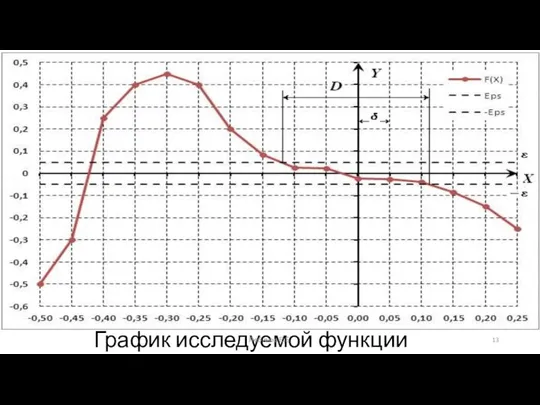
- 13. График исследуемой функции Любимов Е.Б.
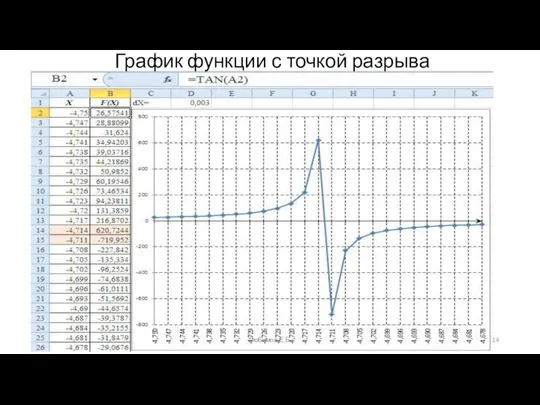
- 14. График функции с точкой разрыва Любимов Е.Б.
- 15. 1a) интервал допустимых изменений аргумента x Є [-∞; +∞]; 1б) В интервале изменения функции Y(x) могут
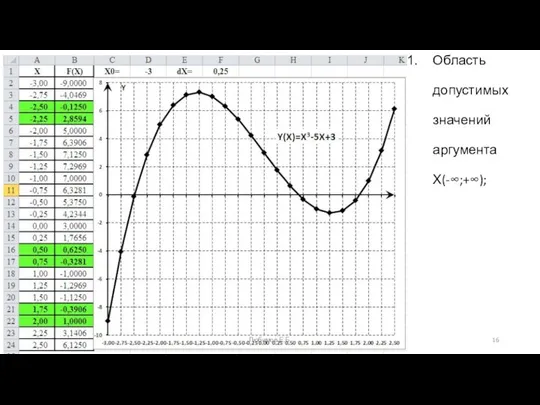
- 16. Область допустимых значений аргумента Х(-∞;+∞); Любимов Е.Б.
- 17. 1-й корень Є(-2,5; -2,25); Y(-2,5) = -0,1250; Y(-2,25) = 2,8594 2-й корень Є(0,5;0,75); Y(0,5) = 0,6250;
- 18. Начальный интервал нахождения корня [a0;b0]: Y(a0)*Y(b0) Алгоритм метода дихотомии (деление пополам) Любимов Е.Б.
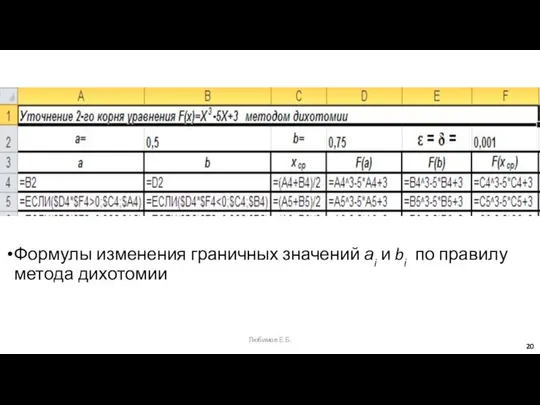
- 19. Реализация метода дихотомии в среде MS Excel Уточнение 2-го корня уравнения F(x)=X3-5X+3 методом дихотомии заголовок таблицы:
- 20. Формулы изменения граничных значений аi и bi по правилу метода дихотомии Заголовок, первая и вторая строки
- 21. Заголовок, первая и вторая строки таблицы (столбцы от F до J) d - длина интервала неопределённости
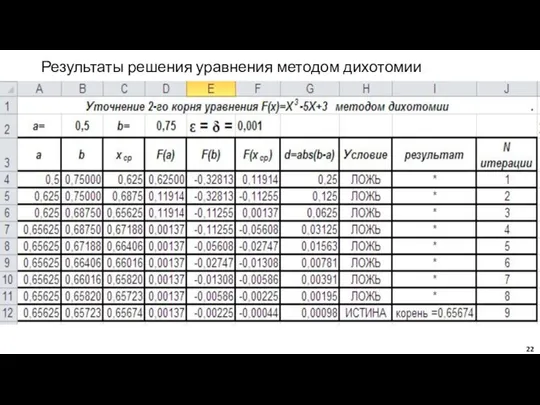
- 22. Результаты решения уравнения методом дихотомии Любимов Е.Б.
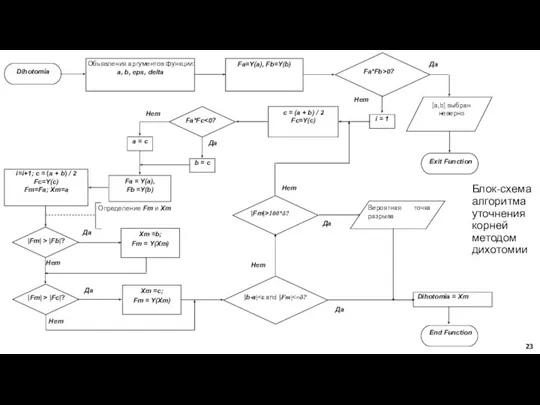
- 23. Блок-схема алгоритма уточнения корней методом дихотомии Любимов Е.Б.
- 24. ' Текст функции Dihotomia с отладочными выводами Public Function Dihotomia(a As Double, b As Double, _
- 25. i = 1 ' вход в цикл определения корня Do ' While ((Abs(b - a) >
- 26. Fm = Fa: Xm = a ' определение точки Xm с наименьшим Y(Xm) If (Abs(Fm) >
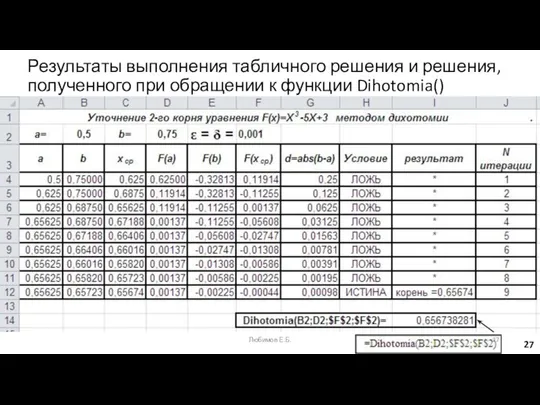
- 27. Результаты выполнения табличного решения и решения, полученного при обращении к функции Dihotomia() Любимов Е.Б.
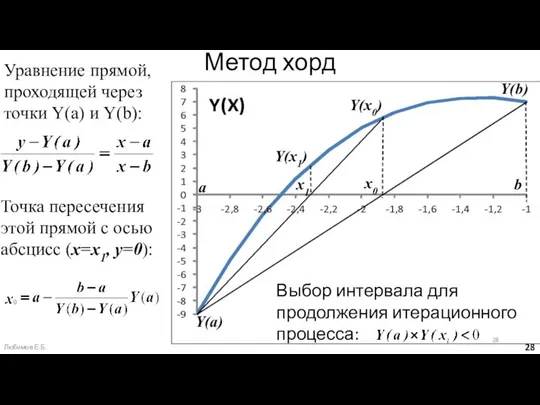
- 28. Метод хорд Уравнение прямой, проходящей через точки Y(a) и Y(b): Точка пересечения этой прямой с осью
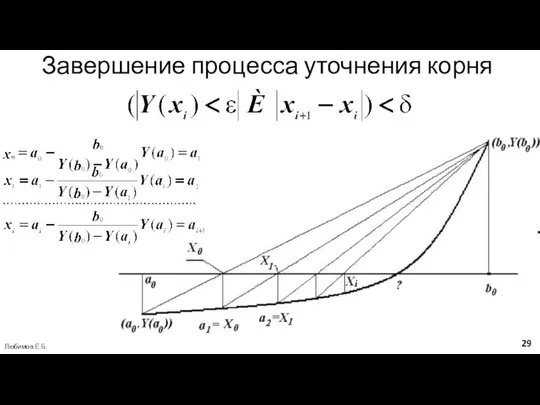
- 29. Завершение процесса уточнения корня Любимов Е.Б.
- 30. Любимов Е.Б.
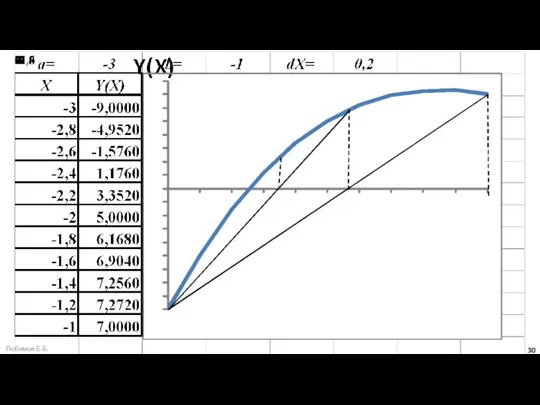
- 31. Реализация метода хорд в среде MS Excel Уточнение 2-го корня уравнения F(x)=X3-5X+3 методом дихотомии заголовок таблицы:
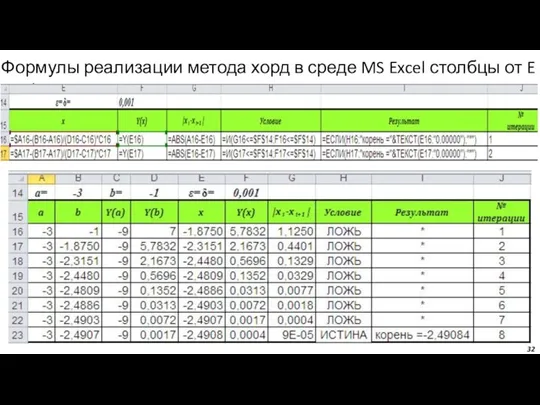
- 32. Любимов Е.Б. Формулы реализации метода хорд в среде MS Excel столбцы от E до J
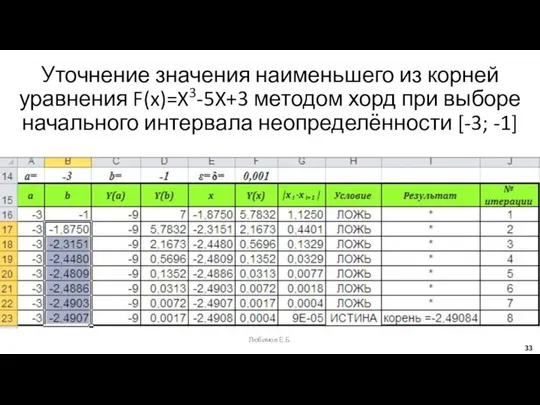
- 33. Уточнение значения наименьшего из корней уравнения F(x)=X3-5X+3 методом хорд при выборе начального интервала неопределённости [-3; -1]
- 35. Скачать презентацию









![Признак нахождения корня в интервале [a; b] Y(a)*Y(b) Обычно решение считается](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1304959/slide-10.jpg)
![1a) интервал допустимых изменений аргумента x Є [-∞; +∞]; 1б) В](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1304959/slide-14.jpg)

![Начальный интервал нахождения корня [a0;b0]: Y(a0)*Y(b0) Алгоритм метода дихотомии (деление пополам) Любимов Е.Б.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1304959/slide-17.jpg)






 Социальные общности, как политические акторы
Социальные общности, как политические акторы Выпуклый анализ. Выпуклое программирование. Лекция 26
Выпуклый анализ. Выпуклое программирование. Лекция 26 Русско-казахский словарь. Орысша-қазақша сөздік
Русско-казахский словарь. Орысша-қазақша сөздік Методика расследования краж
Методика расследования краж  Как собирать средства в ВКонтакте. Инструкция для мам
Как собирать средства в ВКонтакте. Инструкция для мам TOP 10 journalists hailing from Lviv
TOP 10 journalists hailing from Lviv Способы и особенности бетонирования
Способы и особенности бетонирования История возникновения аудита
История возникновения аудита  Стохастические игры
Стохастические игры  Правовий статус пацієнтів в Україні
Правовий статус пацієнтів в Україні Как совершается Таинство Крещения
Как совершается Таинство Крещения Сроки. Исковая давность
Сроки. Исковая давность  Кейнсианская теория Выполнила: Лазарюк А.С. Группа Т-104
Кейнсианская теория Выполнила: Лазарюк А.С. Группа Т-104 ROLLING STONES (Роллинг Стоунз)
ROLLING STONES (Роллинг Стоунз) Les provinces francaises
Les provinces francaises Презентация на тему "Безопасность детей на дороге" - скачать презентации по Педагогике
Презентация на тему "Безопасность детей на дороге" - скачать презентации по Педагогике Свойства функции У = sin x и ее график - презентация по Алгебре_
Свойства функции У = sin x и ее график - презентация по Алгебре_ Портрет в творчестве М.Г. Селищева
Портрет в творчестве М.Г. Селищева Строки
Строки Работа в среде Турбо Паскаль. Составление программ с использованием процедур.
Работа в среде Турбо Паскаль. Составление программ с использованием процедур. Презентация Теория игр
Презентация Теория игр АНКОР Аудит расчетов с персоналом
АНКОР Аудит расчетов с персоналом Хакеры. История появления
Хакеры. История появления Л2_Фотометрия_Бугера_Ламберта_Бера
Л2_Фотометрия_Бугера_Ламберта_Бера «ОРГАНИЗАЦИЯ ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИ В НАЧАЛЬНОЙ ШКОЛЕ»
«ОРГАНИЗАЦИЯ ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИ В НАЧАЛЬНОЙ ШКОЛЕ» Экономический анализ и его роль к управлении ком организациями
Экономический анализ и его роль к управлении ком организациями Служебная документация для внутреннего пользования
Служебная документация для внутреннего пользования Корпоративное бизнес обучение активным продажам на по методике бизнес тренера Иосифа Хусенского
Корпоративное бизнес обучение активным продажам на по методике бизнес тренера Иосифа Хусенского