Содержание
- 2. ВОПРОС 12: Дискретные случайные величины
- 3. Определение: ξ – дискретная случайная величина, если: R(ξ)= {x1, x2, ..., xn, ... } V {x1,
- 4. Пример 1: Свойство: x p(x) 1 6 2 3 4 5
- 5. Пример 2 случайная величина - число наступления события A при одном испытании, причем P(A)=p.
- 6. Биномиальное распределение
- 7. Распределение Пуассона
- 8. Распределение Лапласа
- 9. Пример. На завод прибыла партия деталей в количестве 1000 шт. Вероятность того, что деталь окажется бракованной,
- 10. Пример. Телефонистка в среднем за один час получает N вызовов. Какова вероятность Р(k) того, что в
- 11. РЯД РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
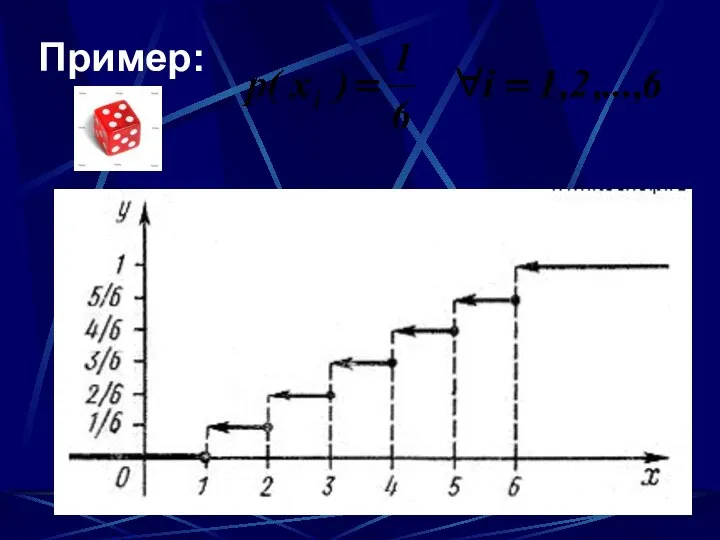
- 12. Пример. ] ξ — число наступлений события (А: s=1) при десяти бросаниях игральной кости. Ряд распределения
- 14. ВОПРОС 13: Функция распределения вероятностей случайной величины и ее свойства
- 15. Определение: называется функцией распределения вероятностей. Функция
- 16. Пример:
- 18. Пример:
- 21. Основные свойства функции распределения 1. 3. 2. =>
- 22. ВОПРОС 14: Непрерывные случайные величины
- 24. Определение: Случайная величина ξ называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция
- 25. СВОЙСТВА F(x) 1. 2. 3.
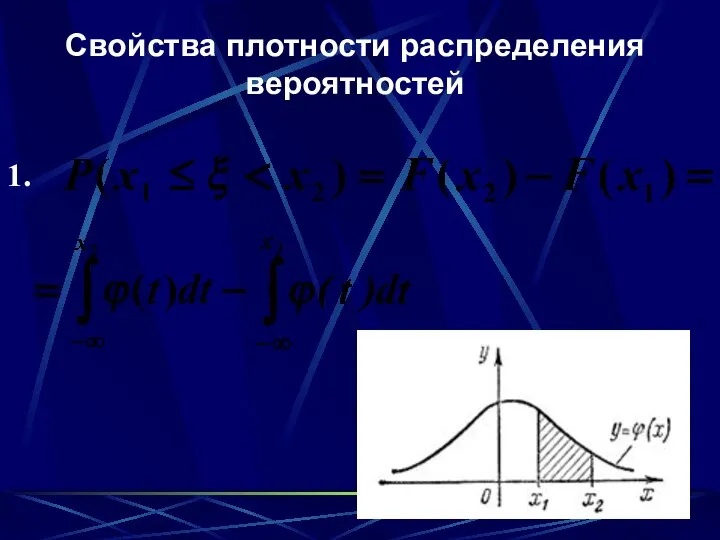
- 26. Свойства плотности распределения вероятностей 1.
- 27. 2. 3.
- 28. . Теорема. Вероятность того, что непрерывная случайная величина может принять любое отдельное значение х, равна нулю.
- 29. Следствие. События, заключающиеся в выполнении каждого из неравенств , , имеют одинаковую вероятность
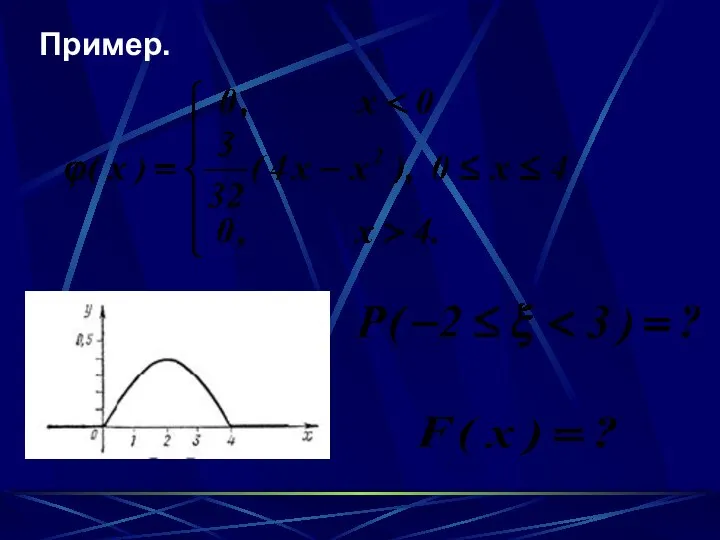
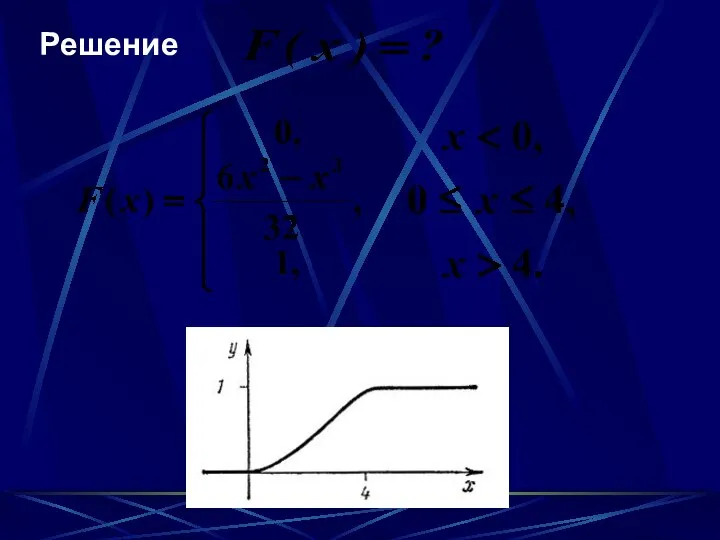
- 30. Пример.
- 31. Решение
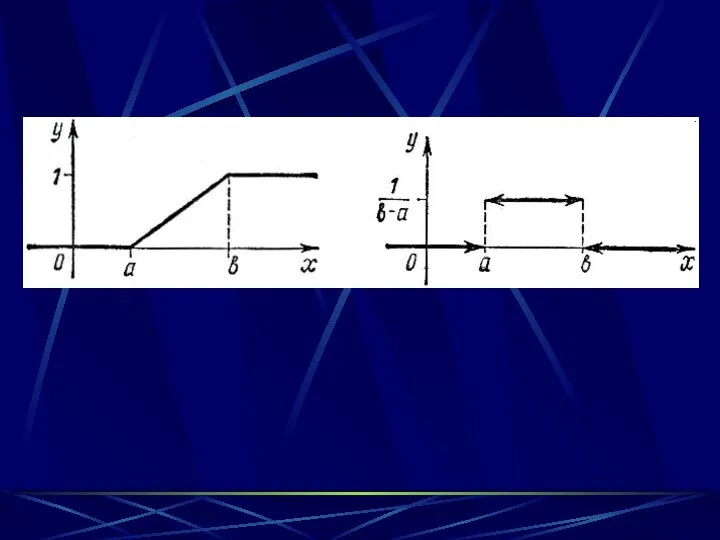
- 32. ВОПРОС 15: Равномерное распределение
- 34. Зоччиэдр Тетраэдр Октаэдр Додакаэдр ИГРАЛЬНЫЕ КОСТИ - АСТРАГАЛЫ Изобретение Паламеда Куб
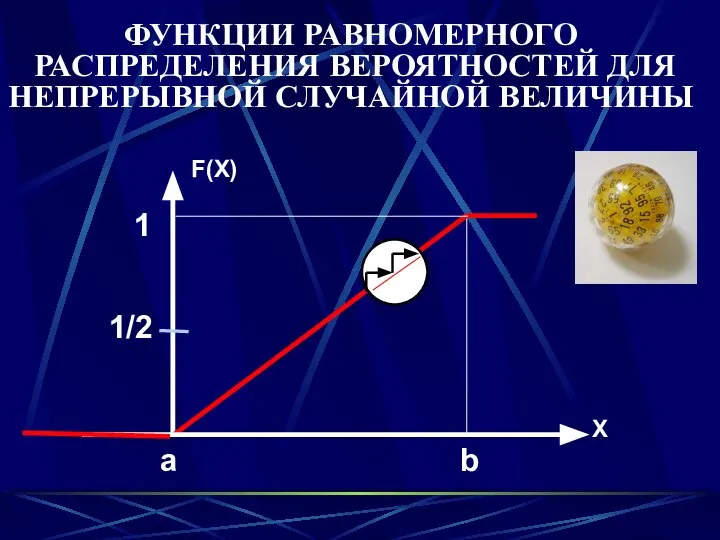
- 35. X F(X) a b ФУНКЦИИ РАВНОМЕРНОГО РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ ДЛЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
- 36. Случайная величина имеет равномерное распределение на отрезке [a, b], т.е. ξ∈U[a, b] («uniform»), если ξ —
- 38. ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
- 40. ВОПРОС 16: Нормальное распределение
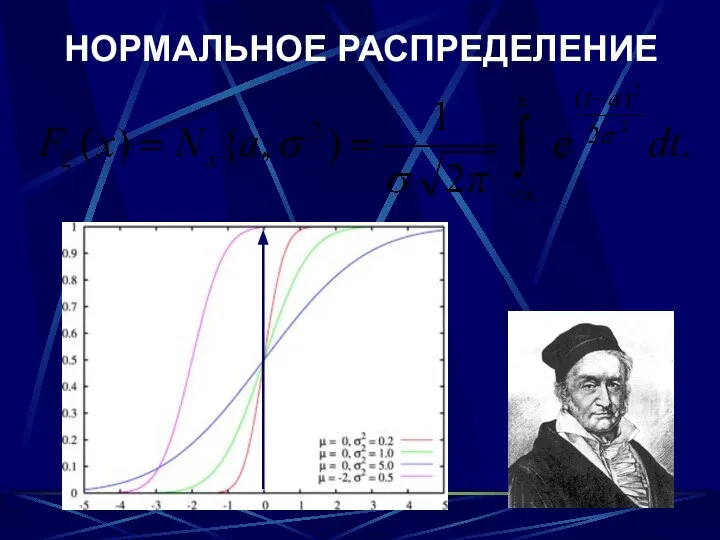
- 41. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- 42. Иоганн Карл Фридрих Гаусс (1777, Брауншвейг —1855, Гёттинген) — немецкий математик, астроном и физик , считается
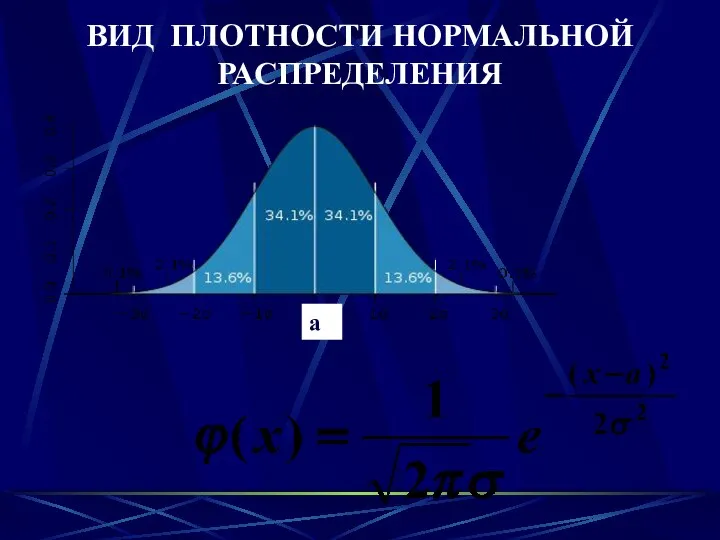
- 43. ВИД ПЛОТНОСТИ НОРМАЛЬНОЙ РАСПРЕДЕЛЕНИЯ
- 44. ВИД ПЛОТНОСТИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
- 45. Свойства при x=a График имеет точки перегиба при При график функции асимптотически приближается к оси Ox
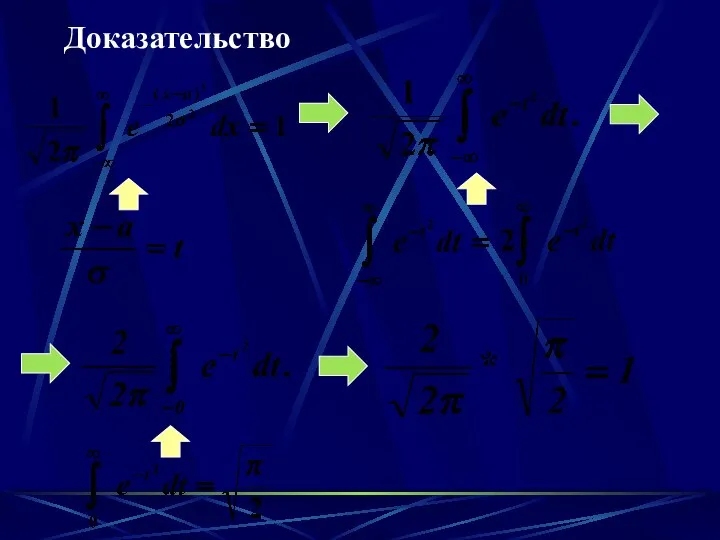
- 46. Теорема. Функция удовлетворяет условию нормировки для любых a и
- 47. Доказательство
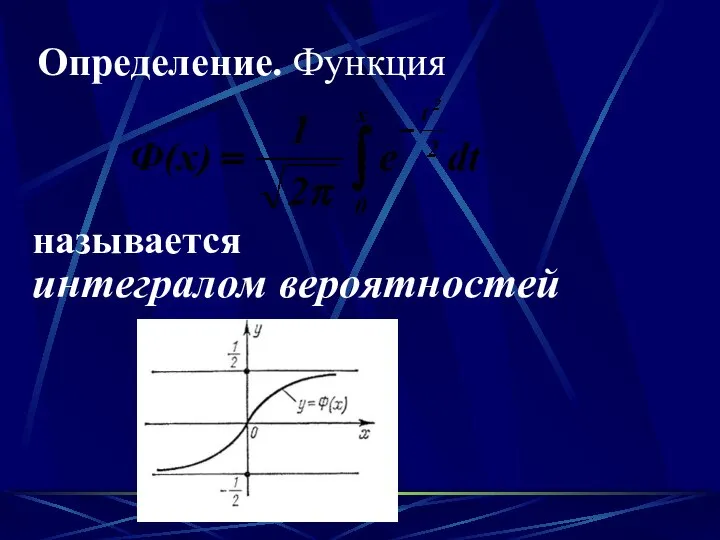
- 48. Определение. Функция называется интегралом вероятностей
- 49. Свойства интеграла вероятностей 1. 2. 4. Ф(0)=0 Ф(-x)=-Ф(х) 3.
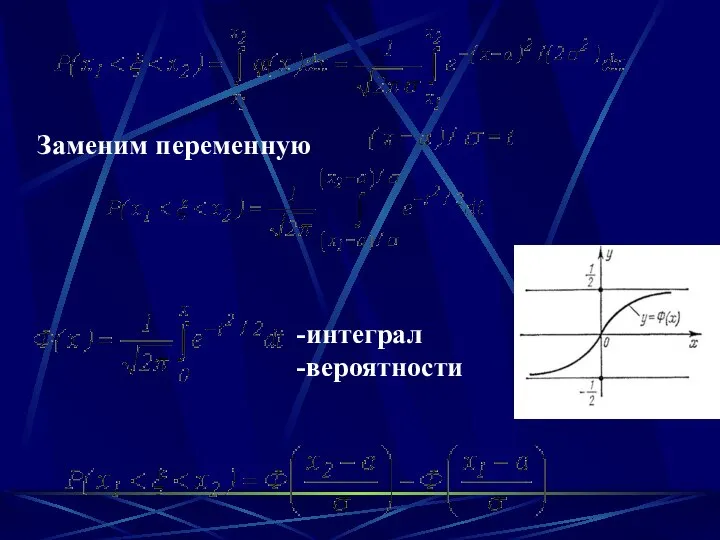
- 50. . Утверждение. Доказательство
- 51. Заменим переменную интеграл вероятности
- 53. =
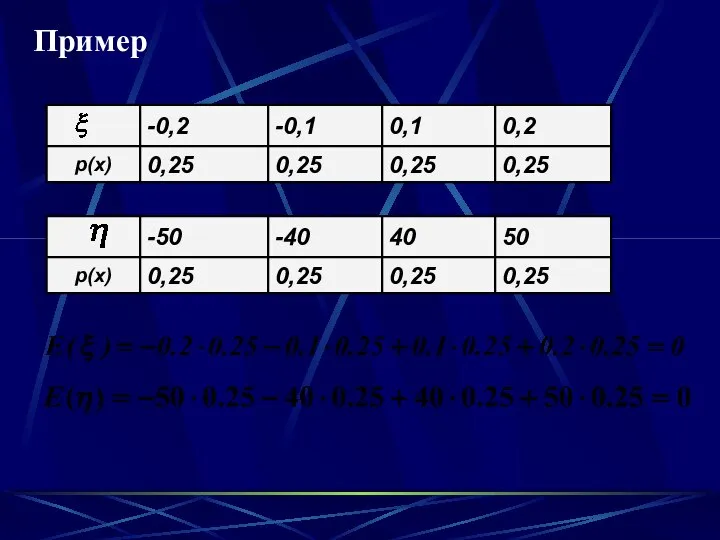
- 55. Пример
- 56. ВОПРОС 17: Математическое ожидание случайной величины и его свойства
- 57. ПРИМЕР. В БД хранится N файлов: m1 - число файлов объемом х1 кб, m2 - файлов
- 58. Определение: Для непрерывной случайной величины
- 59. СВОЙСТВА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
- 60. Пример доказательства
- 61. Замечание 1 ] x1, x2, ..., xn, ... – бесконечная последовательность Требуется, чтобы этот ряд абсолютно
- 62. ВОПРОС 18: Дисперсия и ее свойства. Среднее квадратическое отклонение
- 63. Пример
- 64. Определение:
- 65. Утверждение. Доказательство.
- 66. 1. 2. 3. СВОЙСТВА ДИСПЕРСИИ:
- 67. . Определение:
- 68. ВОПРОС 19: Моменты распределения случайных величин
- 69. Определение. Начальным моментом k-го порядка случайной величины X называется математическое ожидание k-й степени этой случайной величины:
- 71. Определение. Центральным моментом k-го порядка случайной величины X называется математическое ожидание k-й степени центрированной случайной величины
- 73. ВОПРОС 20: Примеры вычисления моментов
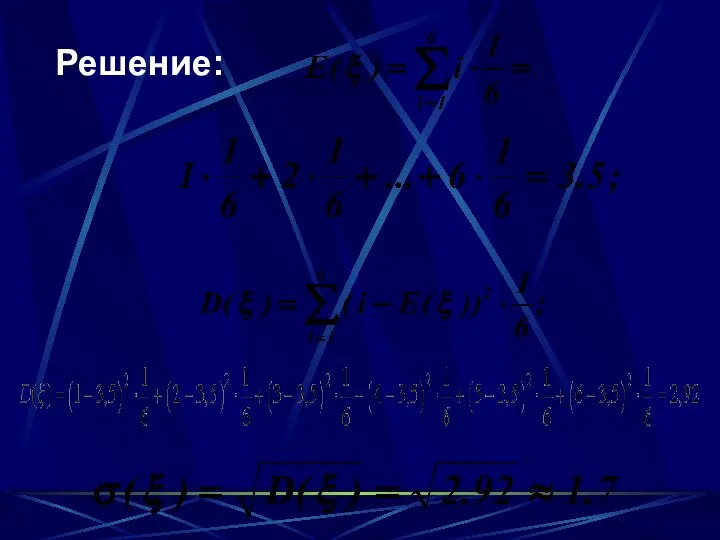
- 74. Пример 1: Случайная величина - число очков, выпадающих при однократном бросании игральной кости. Определить: математическое ожидание,
- 75. Решение:
- 76. Пример 2: Найти математическое ожидание и дисперсию.
- 77. Пример 3: . ,
- 79. Пример 4: Случайная величина распределенная подчинена закону Пуассона Найти:
- 80. Пример 5: Случайная величина распределенная подчинена равномерному закону Найти математическое ожидание, дисперсию и средне квадратическое отклонение
- 82. Пример 6: Случайная величина распределенная подчинена нормальному закону Найти математическое ожидание, дисперсию и средне квадратическое отклонение
- 83. Доказать самостоятельно!
- 84. ВОПРОС 21: Линейные функции случайных величин
- 85. Линейная функция гауссовской (нормально распределенной) случайной величины
- 86. Доказательство. Замена переменной
- 89. Скачать презентацию










![Пример. ] ξ — число наступлений события (А: s=1) при десяти](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301231/slide-11.jpg)






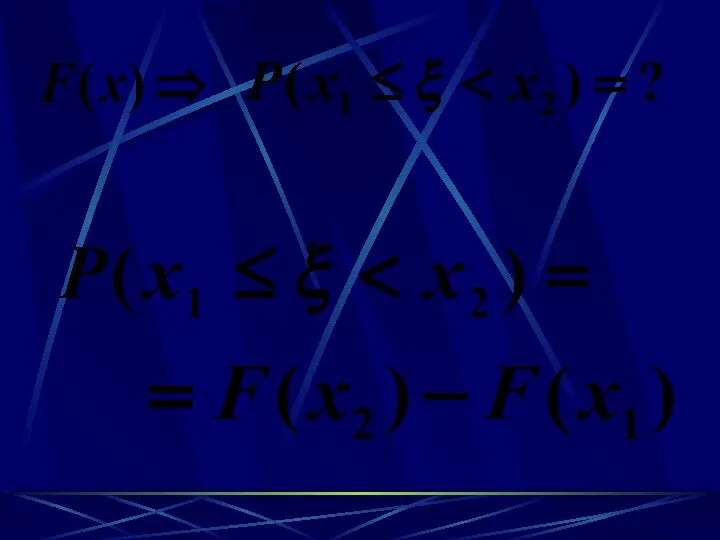










![Случайная величина имеет равномерное распределение на отрезке [a, b], т.е. ξ∈U[a,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301231/slide-35.jpg)










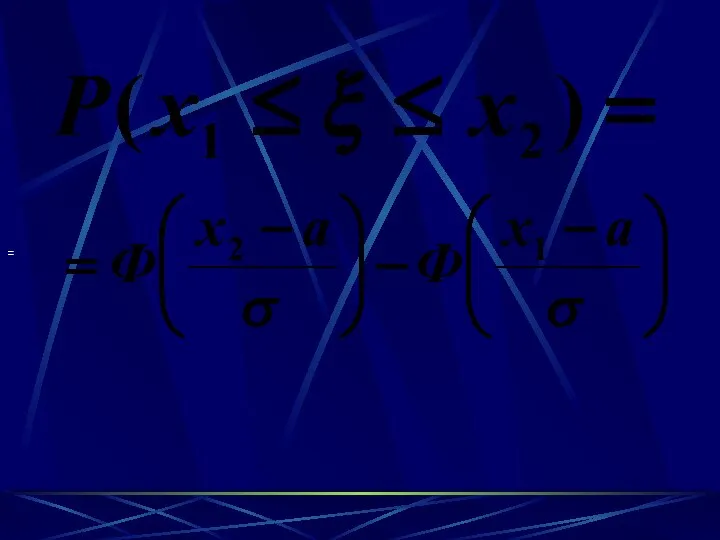







![Замечание 1 ] x1, x2, ..., xn, ... – бесконечная последовательность](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301231/slide-60.jpg)



















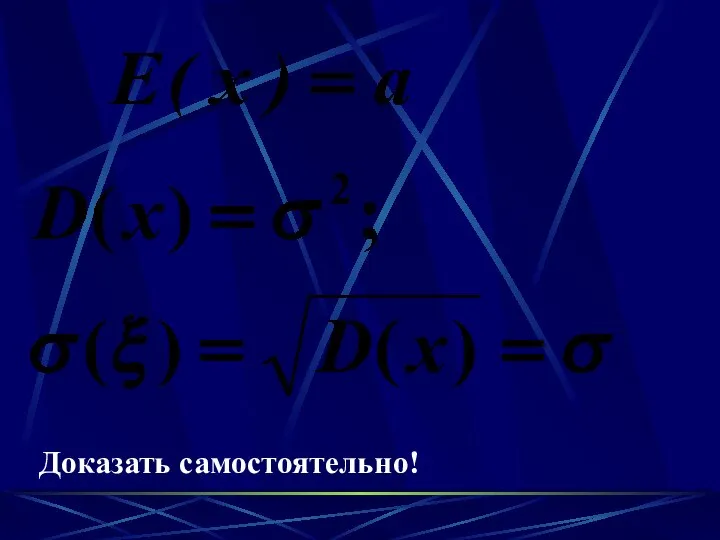




 4.2-Служба-трансфузиологии-многопрофильной-больницы
4.2-Служба-трансфузиологии-многопрофильной-больницы Pathways RTK and GPCR
Pathways RTK and GPCR Сайти інтернете
Сайти інтернете Отделочные работы
Отделочные работы Чемпионы мира по шахматам. Сильнейшие шахматисты от древности до наших дней
Чемпионы мира по шахматам. Сильнейшие шахматисты от древности до наших дней Строки Паскаль. Чем плох массив символов?
Строки Паскаль. Чем плох массив символов? ДЕРЖАВНІСТЬ ТА ДЕРЖАВНЕ УПРАВЛЯННЯ ЕКОНОМІКИ
ДЕРЖАВНІСТЬ ТА ДЕРЖАВНЕ УПРАВЛЯННЯ ЕКОНОМІКИ Внимательно слушайте – и всё услышите! Внимательно смотрите – и всё увидите! Думайте – и всё обязательно поймёте! Внимательно
Внимательно слушайте – и всё услышите! Внимательно смотрите – и всё увидите! Думайте – и всё обязательно поймёте! Внимательно  Мишель Фуко. Теория глагола
Мишель Фуко. Теория глагола Презентация по алгебре Алгебраические методы решения прикладных задач на экстремум
Презентация по алгебре Алгебраические методы решения прикладных задач на экстремум А ты знаешь как все начиналось? - презентация
А ты знаешь как все начиналось? - презентация Батик
Батик Орфограммы в суффиксах существительных
Орфограммы в суффиксах существительных  Формы самостоятельных занятий
Формы самостоятельных занятий АПИРОГ. ВОДА С КАРТИНКАМИ
АПИРОГ. ВОДА С КАРТИНКАМИ Интересные факты из жизни великих женщин-математиков
Интересные факты из жизни великих женщин-математиков Электроника NexGen
Электроника NexGen Медицина эпохи рабовладения
Медицина эпохи рабовладения Волшебный узелок
Волшебный узелок Поэтика Марины Цветаевой
Поэтика Марины Цветаевой Общественное служение христианина
Общественное служение христианина Звіт про роботу в конкурсах - презентация для начальной школы_
Звіт про роботу в конкурсах - презентация для начальной школы_ Эстетика Ренессанса
Эстетика Ренессанса Презентация по физкультуре Легкая атлетика организация соревнований
Презентация по физкультуре Легкая атлетика организация соревнований Ислам _
Ислам _ 2 класс 2 четверть Авторы: Хомутовская Л.Н., МОУ Саваслейская ср. шк. Каргина В.В., МОУ Новосельская ср. шк. 2005
2 класс 2 четверть Авторы: Хомутовская Л.Н., МОУ Саваслейская ср. шк. Каргина В.В., МОУ Новосельская ср. шк. 2005 Т р у х а н о в отдых & развлечения банкет-холл
Т р у х а н о в отдых & развлечения банкет-холл Особенности программирования на объектно-ориентированных языках
Особенности программирования на объектно-ориентированных языках