Содержание
- 2. Первая (основная) теорема двойственности Теорема: Если одна из сопряженных задач имеет оптимальное решение, то и вторая
- 3. Вторая теорема двойственности Теорема: Для того чтобы два допустимых решения и пары двойственных задач были их
- 4. Правила построения двойственных задач: 1. Если в исходной задаче целевая функция исследуется на min, то в
- 5. 4. Матрица ограничений двойственной задачи получается из матрицы ограничений исходной задачи транспонированием. 5. Если в исходной
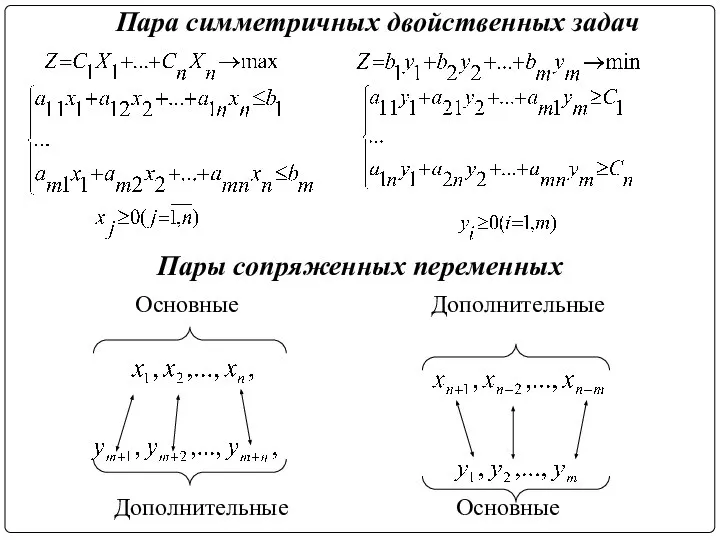
- 6. Пара симметричных двойственных задач Пары сопряженных переменных Основные Дополнительные Дополнительные Основные
- 7. Важно знать Объективно обусловленные оценки ресурсов определяют степень дефицитности ресурсов: по оптимальному плану производства дефицитные (т.е.
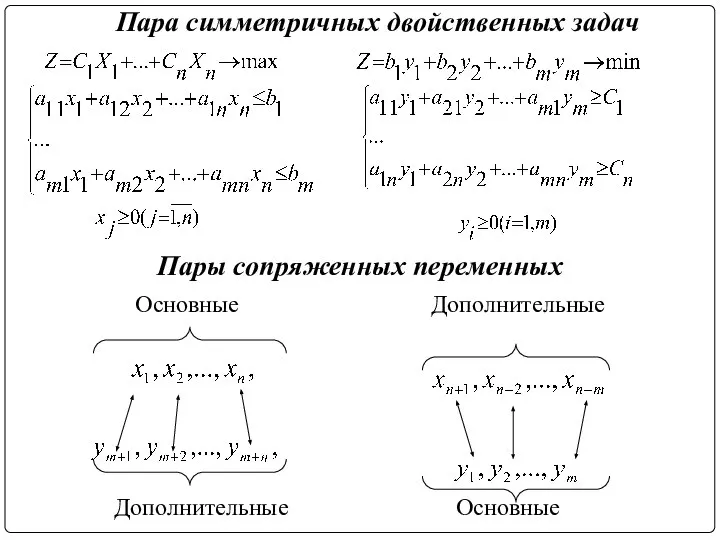
- 8. Пара симметричных двойственных задач Пары сопряженных переменных Основные Дополнительные Дополнительные Основные
- 9. Экономический смысл основной теоремы двойственности План производства и набор цен ресурсов оказываются оптимальными тогда и только
- 10. Исследование на устойчивость Исследование на устойчивость – исследование диапазона изменения правых частей системы ограничений, при котором
- 12. Скачать презентацию







 Особые точки ФКП
Особые точки ФКП Бизнес план. Дизайнерское агенство «ИнтерСтудия»
Бизнес план. Дизайнерское агенство «ИнтерСтудия» Радиационная безопасность
Радиационная безопасность  Леонардо да Винчи - анатом
Леонардо да Винчи - анатом Русский народный костюм
Русский народный костюм Презентация Нормативно-правовая база внебюджетных фондов РФ
Презентация Нормативно-правовая база внебюджетных фондов РФ Одежда программа «Планета Знаний» окружающий мир 1 класс
Одежда программа «Планета Знаний» окружающий мир 1 класс  Презентацию подготовила ученица 4 Б класса ГОУ СОШ № 2031 Домненко Екатерина
Презентацию подготовила ученица 4 Б класса ГОУ СОШ № 2031 Домненко Екатерина Загадки о спецмашинах. - презентация для начальной школы_
Загадки о спецмашинах. - презентация для начальной школы_ Уроки Вождения. Автоинструктор
Уроки Вождения. Автоинструктор Коровина Анастасия Осень. Осень. Не виден больше солнца луч, Не виден больше солнца луч, На небе только стая туч На небе только стая
Коровина Анастасия Осень. Осень. Не виден больше солнца луч, Не виден больше солнца луч, На небе только стая туч На небе только стая  Олимпийский чемпион. Нелёгкая победа Легкова
Олимпийский чемпион. Нелёгкая победа Легкова Презентация Социальная поддержка лиц находящихся в академическом отпуске по медицинским показаниям
Презентация Социальная поддержка лиц находящихся в академическом отпуске по медицинским показаниям  Перспективы развития Руси Матушки
Перспективы развития Руси Матушки ARKAN - Федеральный оператор безопасности
ARKAN - Федеральный оператор безопасности Орфограммы парных по глух-звон согласных
Орфограммы парных по глух-звон согласных Школьное питание в МБОУ «Вишневская НОШ» 2014-2015 учебный год Беловский район, с.Вишневка.
Школьное питание в МБОУ «Вишневская НОШ» 2014-2015 учебный год Беловский район, с.Вишневка. ИЗОБРАЗИТЕЛЬНОЕ ИСКУССТВО ЖАНРЫ ЖИВОПИСИ
ИЗОБРАЗИТЕЛЬНОЕ ИСКУССТВО ЖАНРЫ ЖИВОПИСИ Система органов государственной власти
Система органов государственной власти Доклад про монастырь "Оптина Пустынь"
Доклад про монастырь "Оптина Пустынь" Александр Александрович Дейнека
Александр Александрович Дейнека Система управления качеством
Система управления качеством Христианство
Христианство Система каротажа при бурении. Занятие 9
Система каротажа при бурении. Занятие 9 Исторический обзор развития плавания
Исторический обзор развития плавания Домашние животные - презентация для начальной школы
Домашние животные - презентация для начальной школы Элитарная литература Элитарная литература - это высокодуховные произведения, заставляющие переживать и думать. Каждое такое прои
Элитарная литература Элитарная литература - это высокодуховные произведения, заставляющие переживать и думать. Каждое такое прои Тема урока: Как ухаживать за кошкой
Тема урока: Как ухаживать за кошкой