Ферромагнетизм

(21.1.1)

(21.1.2)

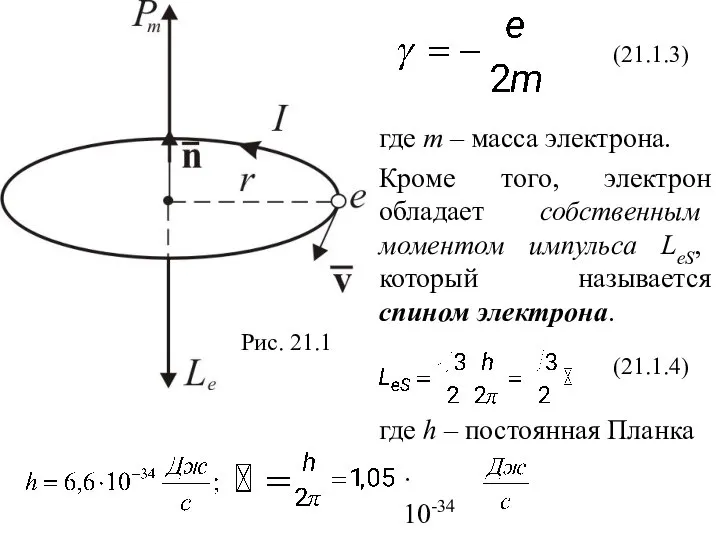
Рис. 21.1

(21.1.3)

(21.1.4)

· 10-34

(21.1.5)

(21.1.6)

(21.1.7)

(21.1.8)

(21.1.9)

(21.2.3)

(21.2.2)

(21.2.1)

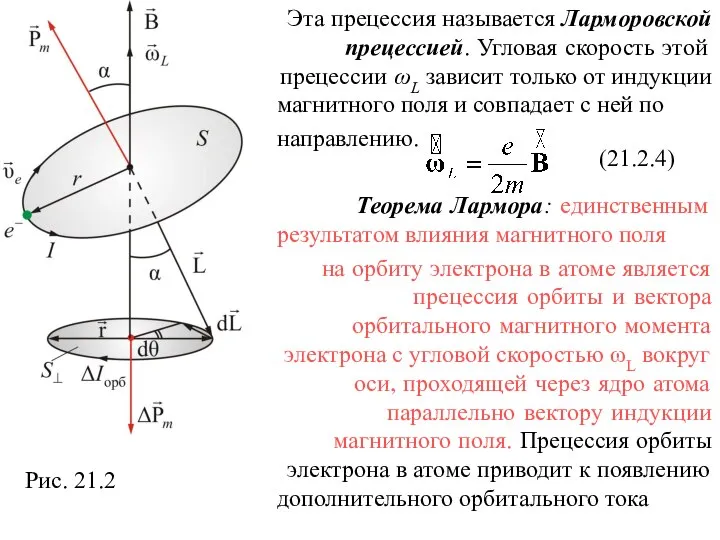
Рис. 21.2

(21.2.4)

(21.2.5)

(21.2.6)

(21.2.7)

(21.3.1)

(21.3.2)

(21.3.3)

13.4. Магнитное поле в веществе

(21.4.1)

(21.4.2)

(21.4.4)

Рис21.3

(21.4.5)

(21.4.6)

(21.4.7)

(21.4.8)

(21.4.9)

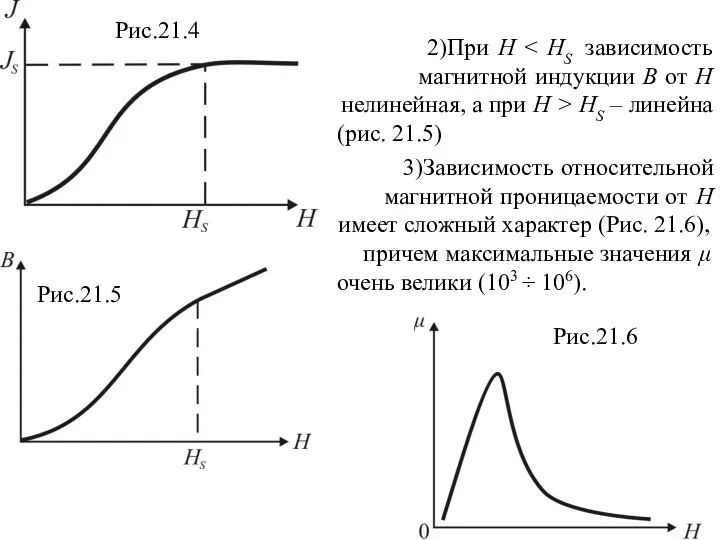
Рис.21.4

Рис.21.5

Рис.21.6

Рис.21.7

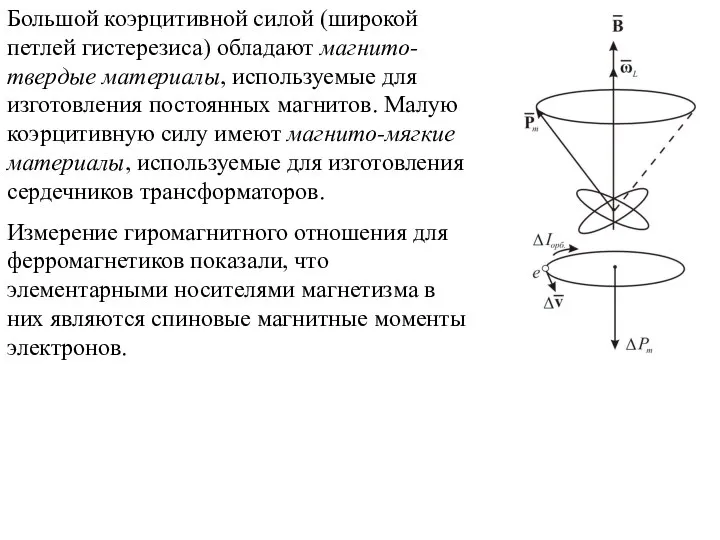
Большой коэрцитивной силой (широкой петлей гистерезиса) обладают магнито-твердые материалы, используемые для

Рис. 15.1,а

(15.1.5)

(15.1.6)

(15.1.7)

(15.1.8)

(15.1.9)

Лекция

Тема: УРАВНЕНИЯ МАКСВЕЛЛА

Введение
2. Уравнения Максвелла в интегральной – дифференциальной формах

1. Введение

2. Уравнения Максвелла в интегральной – дифференциальной формах

(1)

(2)

,

,

,

(3)

(4)

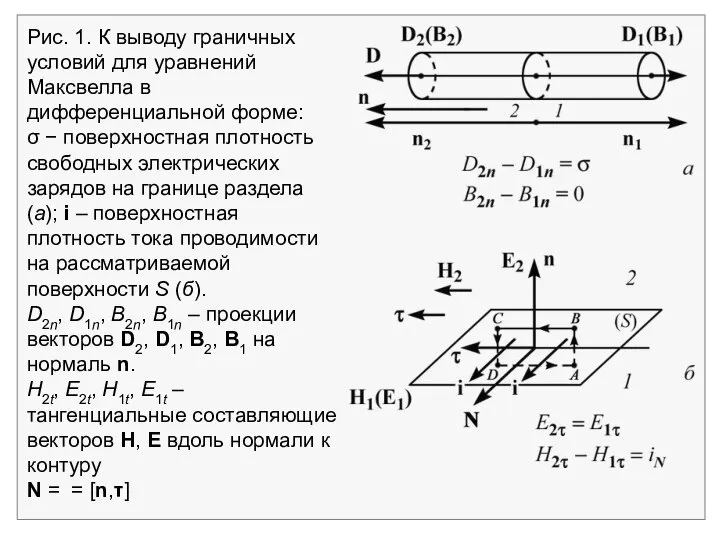
Рис. 1. К выводу граничных условий для уравнений Максвелла в дифференциальной