Содержание
- 2. ВВЕДЕНИЕ Гидродинамика – наука о поведении жидкостей в различных условиях. Основные проблемы гидродинамики – изучение течений
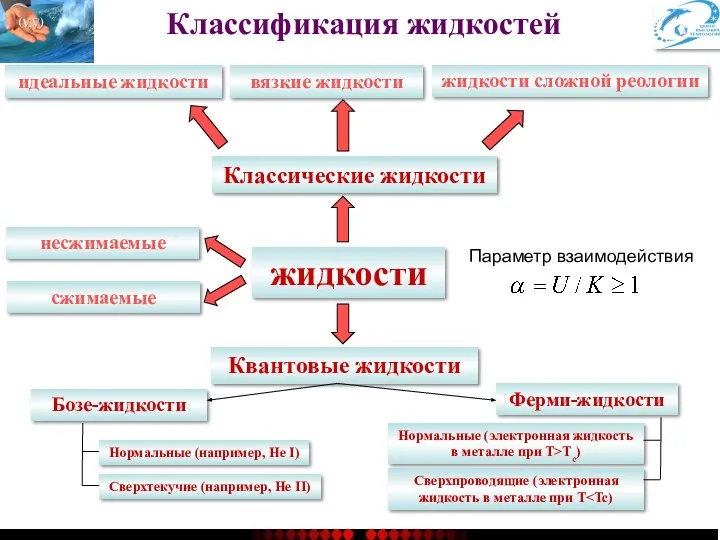
- 3. Классификация жидкостей жидкости идеальные жидкости вязкие жидкости жидкости сложной реологии Бозе-жидкости Ферми-жидкости Классические жидкости несжимаемые Квантовые
- 4. Модели гидродинамики классических жидкостей Идеальная жидкость: пренебрегается всеми процессами релаксации – вязкостью, теплопроводностью и т.д. Вязкая
- 5. Идеальная жидкость: пренебрегается всеми процессами диссипации – вязкостью, теплопроводностью и т.д. Отсутствие диссипации энергии в жидкости
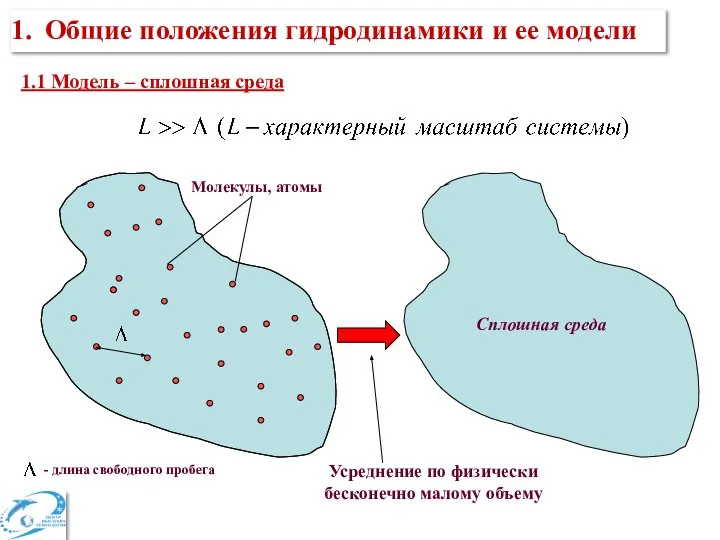
- 6. Общие положения гидродинамики и ее модели 1.1 Модель – сплошная среда Молекулы, атомы - длина свободного
- 7. От координат и скоростей отдельных частиц (атомов, молекул, …) – переход к макроскопическим параметрам – скорости,
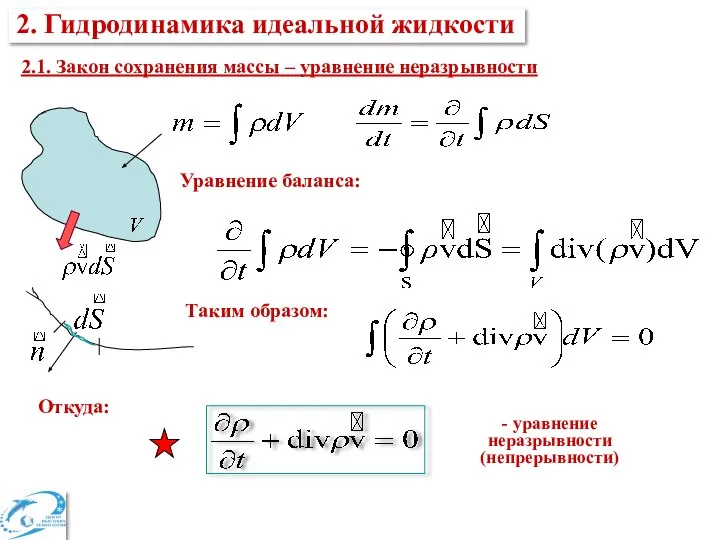
- 8. 2. Гидродинамика идеальной жидкости 2.1. Закон сохранения массы – уравнение неразрывности Уравнение баланса: Таким образом: Откуда:
- 9. 2.2. Закон сохранения импульса – уравнение Эйлера Леонард Эйлер 1707 - 1783 Полная сила, действующая на
- 10. Отсюда получаем: уравнение движения (закон сохранения импульса), уравнение Эйлера, 1755г. Леонард Эйлер 1707 - 1783 Если
- 11. Уравнения идеальной жидкости содержат пять скалярных функций: три компоненты скорости; плотность; давление. Таким образом, эти пять
- 12. 2.3. Гидростатика Если жидкость покоится, то из уравнения Эйлера следует, что В однородном поле тяжести Откуда:
- 13. 2.4. Стационарные течения, уравнение Бернулли Важным случаем гидродинамических течений являются стационарные (установившиеся) течения. В таких течениях
- 14. Получаем: Откуда: Введем понятие о линиях тока: Линии тока – линии, касательные к которым указывают направление
- 15. Отсюда следует, что Последнее уравнение носит название уравнения Бернулли (1738г.) Даниил Бернулли (1667-1748) Если течение жидкости
- 16. 2.5. Поток энергии Вычислим изменение со временем энергию единичного объема жидкости - сумма кинетической и внутренней
- 17. Отсюда можно записать (используя соотношение адиабатичности ds/dt=0): Окончательно можно записать: Проинтегрируем полученное выражение по объему: -
- 18. Информация к размышлению: Вектор потока энергии показывает, что каждая частица жидкости переносит при своем движении энергию
- 19. 2.6. Поток импульса Вычислим изменение со временем импульса единичного объема жидкости. Будем пользоваться тензорными обозначениями. Запишем
- 20. Тогда получим Тензор Пik определяется так: Тензор Пik является симметричным, т.е. Чтобы выяснить физический смысл тензора
- 21. Комментарий: величина есть i – я компонента импульса, протекающего через элемент поверхности dS; записывая dSk=nkdS, то
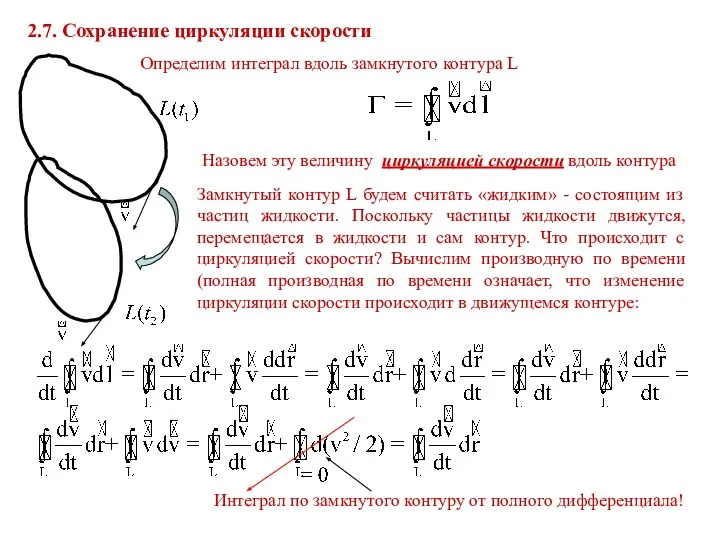
- 22. 2.7. Сохранение циркуляции скорости Определим интеграл вдоль замкнутого контура L Замкнутый контур L будем считать «жидким»
- 23. Таким образом, поскольку из уравнения движения то применяя теорему Стокса (поскольку ), имеем: Откуда окончательно находим:
- 24. Теорема Томсона получена на основе использования уравнения Эйлера, т.е. на базе использования предположения об изоэнтропичности движения
- 25. 2. 8. Потенциальные течения Закон сохранения циркуляции скорости позволяет рассмотреть специальный класс течений в гидродинамике идеальной
- 26. Как и всякое векторное поля с равным нулю ротором, скорость потенциально движущейся жидкости может быть выражена
- 27. Поскольку скорость через потенциал определяется с точностью до произвольной функции от времени, можно положить правую часть
- 28. 2.9. Несжимаемая жидкость Важным случаем гидродинамических течений является ситуация, когда плотность жидкости можно считать постоянной (при
- 29. Уравнение Бернулли тоже может быть записано для несжимаемой жидкости в более простом виде: Для потенциального течения
- 30. Условие несжимаемости жидкости При адиабатическом течении изменение плотности связано с изменением давления: Согласно уравнению, колебания давления
- 31. В нестационарно движущейся жидкости необхожимо для несжимаемости выполнение еще одного условия. Пусть - величины порядка масштабов
- 33. Скачать презентацию


























 Функции таможенных органов Работу выполнил Студент группы Т-111 Бобырь Алексей
Функции таможенных органов Работу выполнил Студент группы Т-111 Бобырь Алексей The political system of Great Britain
The political system of Great Britain Завод «Кундуз» Презентация медиа-кампании
Завод «Кундуз» Презентация медиа-кампании Готов к труду и обороне
Готов к труду и обороне Закон Вебера-Фехнера
Закон Вебера-Фехнера Suomen kielen tunnit
Suomen kielen tunnit St. Valentine’s Day
St. Valentine’s Day Олимпийское движение в Беларуси
Олимпийское движение в Беларуси Государственная кадастровая оценка земель сельскохозяйственного назначения. Методическое и технологическое обеспечение оценки
Государственная кадастровая оценка земель сельскохозяйственного назначения. Методическое и технологическое обеспечение оценки Теория Жана Пиаже
Теория Жана Пиаже Выполнение основных операций штукатурных процессов
Выполнение основных операций штукатурных процессов Современные материалы в строительстве
Современные материалы в строительстве Тайны грибного царства - презентация для начальной школы_
Тайны грибного царства - презентация для начальной школы_ Опусти свой стакан
Опусти свой стакан Герои сошли со страниц литературных произведений Презентация на тему:_
Герои сошли со страниц литературных произведений Презентация на тему:_ Форма государства Политическая система общества
Форма государства Политическая система общества Презентация "Профессия – «Экономист»" - скачать презентации по Экономике
Презентация "Профессия – «Экономист»" - скачать презентации по Экономике Стандарт OpenMP. Информационные ресурсы. Лекция 3
Стандарт OpenMP. Информационные ресурсы. Лекция 3 Презентация на тему История появления бисера
Презентация на тему История появления бисера  Internet tracking
Internet tracking Ислам
Ислам Иван Константинович Айвазовский (1817-1900)
Иван Константинович Айвазовский (1817-1900) Управление моделями в UML
Управление моделями в UML «С» - [s] [k]
«С» - [s] [k] Термодинамический потенциал в переменных S, V
Термодинамический потенциал в переменных S, V Коммерческое предложение для партнёров
Коммерческое предложение для партнёров Понятие психология Выполнила: студентка 1-ого курса ФТД группа Т-116 Цьопа Дарья
Понятие психология Выполнила: студентка 1-ого курса ФТД группа Т-116 Цьопа Дарья Maria Hoefl-Riesch. Bekannte deutsche Sportlerin
Maria Hoefl-Riesch. Bekannte deutsche Sportlerin