Содержание
- 4. 3. Гидродинамика вязкой жидкости Обратимся к случаю, когда необходимо учитывать процессы диссипации в жидкости. В реальных
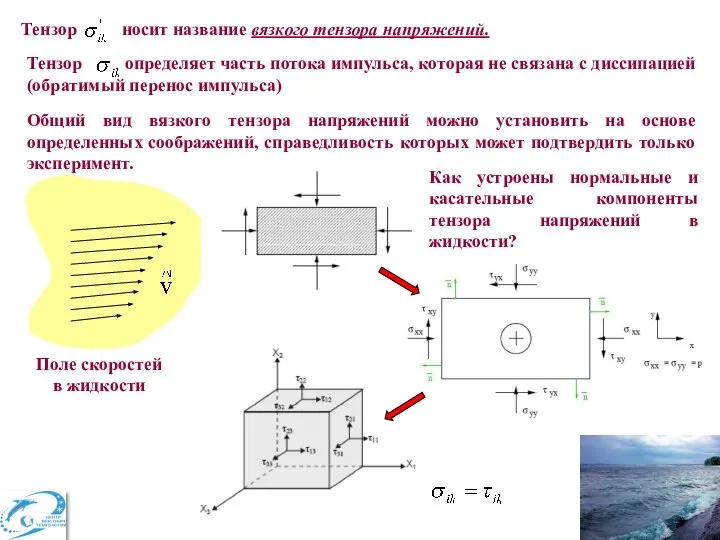
- 5. Тензор носит название вязкого тензора напряжений. Тензор определяет часть потока импульса, которая не связана с диссипацией
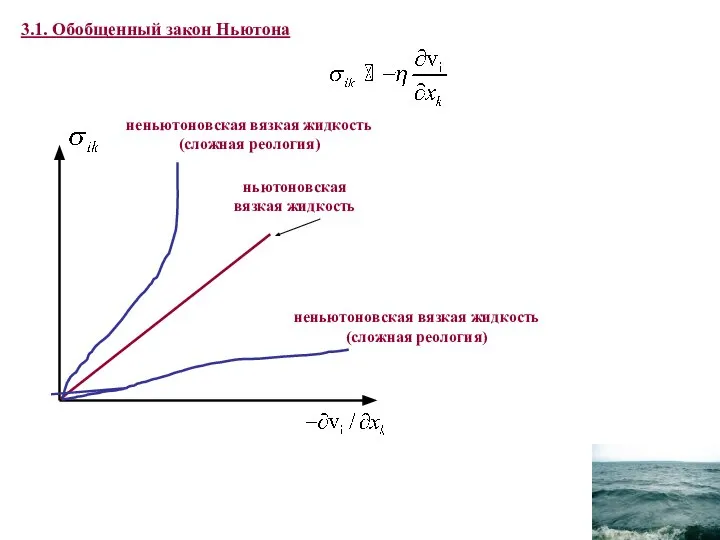
- 6. 3.1. Обобщенный закон Ньютона ньютоновская вязкая жидкость неньютоновская вязкая жидкость (сложная реология) неньютоновская вязкая жидкость (сложная
- 7. 3.2. Вывод уравнений вязкой жидкости Для того, чтобы установить общий вид тензора вязких напряжений, используем следующие
- 8. Здесь коэффициенты , которые не зависят от скорости, называются соответственно коэффициентами первой и второй вязкости. Обе
- 9. C.L.Navier (1785-1836) G.G.Stokes (1819-1903) - уравнение Навье-Стокса (Навье – 1827г. – из модельных соображений; Стокс –
- 10. Для несжимаемой жидкости, аналогично случаю уравнения Эйлера, можно исключить в уравнении Навье-Стокса давление. Применив операцию ротор
- 11. Условие равенства нулю касательной компоненты скорости в макроскопической гидродинамике носит название непроскальзывания (отсутствие скольжения на границе
- 12. Поучение 1. Уравнения Навье-Стокса в различных координатах А. Декартовы прямоугольные координаты:
- 13. Б. Цилиндрические координаты:
- 14. 3.4. Течения вязкой жидкости в каналах 3.4.1. Плоское течение Пусть жидкость находится в плоском канале, одна
- 15. Таким образом, профиль скорости линеен. Средняя скорость жидкости может быть найдена из соотношения: Найдем действующие на
- 16. Откуда давление по координате «y» постоянно: Поскольку давление не зависит от координаты «y», то в первом
- 17. 3.4.3. Течение в трубе (течение Пуазейля) x r 2R Рассмотрим течение вязкой жидкости в цилиндрической трубе.
- 18. Окончательно получаем профиль скорости в трубе - скорость распределена по параболическому закону (пуазейлевский профиль скорости) При
- 19. 3.5. Течения при малых числах Рейнольдса 3.5.1. Законы подобия Важную роль в исследованиях гидродинамики вязкой жидкости
- 20. Аналогичные законы подобия можно сформулировать и для распределения давления и силы сопротивления: 3.5.2. Течения при малых
- 21. 3.5.3. Течение Стокса G.G.Stokes (1819-1903) Рассмотрим прямолинейное и равномерное движение шара в вязкой жидкости (что эквивалентно
- 22. Отсюда получаем, что Из уравнение (3.14) следует (дивергенция скорости равна нулю, что Тогда получаем, что В
- 23. Откуда Окончательно (3.19) Постоянные должны находится из граничных условий , причем Находя константы, получаем решение Стокса
- 24. Выражение для давления в жидкости можно найти, согласно соотношению: Вычислим силу со стороны жидкости, действующую на
- 26. Скачать презентацию




















 Типы шлифовальных станков
Типы шлифовальных станков 14 занятие.ppt
14 занятие.ppt Медико- социальные последствия Чернобыльской аварии Выполнила: Шова Наталья 204Б группа Преподаватель: Русецкий С.В.
Медико- социальные последствия Чернобыльской аварии Выполнила: Шова Наталья 204Б группа Преподаватель: Русецкий С.В. Пронести дар через годы непогасшим. Ко дню рождения А. И. Солженицына
Пронести дар через годы непогасшим. Ко дню рождения А. И. Солженицына Деление чисел - презентация по Алгебре
Деление чисел - презентация по Алгебре Понятие и виды профессиональной этики (сравнительная характеристика административной и деловой этики)
Понятие и виды профессиональной этики (сравнительная характеристика административной и деловой этики) DeVita Ritm mini - цифровое устройство оздоровления
DeVita Ritm mini - цифровое устройство оздоровления 4 U ЗАГОЛОВКИ
4 U ЗАГОЛОВКИ Металлы применяемые в строительстве
Металлы применяемые в строительстве Магазин матрешек. Игра
Магазин матрешек. Игра Конфликт интересов на государственной службе: понятие и содержание
Конфликт интересов на государственной службе: понятие и содержание Дуэли в жизни и творчестве А.С.Пушкина
Дуэли в жизни и творчестве А.С.Пушкина Самураи
Самураи Бюджетное общеобразовательное учреждение города Омска «Средняя общеобразовательная школа № 152 Областное родительское соб
Бюджетное общеобразовательное учреждение города Омска «Средняя общеобразовательная школа № 152 Областное родительское соб Древние языки и культуры. Готский язык
Древние языки и культуры. Готский язык Работа по выверке списков воинских захоронений. Пошаговая инструкция
Работа по выверке списков воинских захоронений. Пошаговая инструкция Innovation project management
Innovation project management «Школа безопасности «Зарница 2019»
«Школа безопасности «Зарница 2019» Одежда говорит о человеке
Одежда говорит о человеке Символы Российской власти
Символы Российской власти Системы с одной степ свободы
Системы с одной степ свободы Цифровое телевидение
Цифровое телевидение ОСОБЕННОСТИ ОЦЕНКИ ФИНАНСОВЫХ ВЛОЖЕНИЙ
ОСОБЕННОСТИ ОЦЕНКИ ФИНАНСОВЫХ ВЛОЖЕНИЙ Архитектура и функциональные возможности Visual Studio Team Foundation Server
Архитектура и функциональные возможности Visual Studio Team Foundation Server Почему шляпы? Шляпу легко надеть и снять, кроме того, шляпы указывают на роль. «Примеряя» на себя шляпу определённого цветы, мы учи
Почему шляпы? Шляпу легко надеть и снять, кроме того, шляпы указывают на роль. «Примеряя» на себя шляпу определённого цветы, мы учи Презентация Разминка по экологии
Презентация Разминка по экологии Краснуха, корь, лекция
Краснуха, корь, лекция  Пищевые отравления
Пищевые отравления