Содержание
- 2. Цели урока Ввести понятие иррациональных уравнений и показать способы их решений. Развивать умение выделять главное, существенное
- 3. Устная работа
- 4. Устная работа Упростить выражение:
- 5. Устная работа Решите уравнения: а) б) в) г) д)
- 7. Тема урока Иррациональные уравнения
- 8. Определение Иррациональными называются уравнения, в которых переменная содержится под знаком корня или под знаком операции возведения
- 9. Устно: Какие из следующих уравнений являются иррациональными? а) х + √ х = 2 б) х
- 10. Посторонние корни Основными причинами появления посторонних корней является возведение обеих частей уравнения в одну и ту
- 11. Метод возведения обеих частей уравнения в одну и ту же степень Преобразовать обе части уравнения к
- 12. Примеры
- 13. Если квадратных корней в иррациональном уравнении много, то приходится возводить в квадрат несколько раз:
- 15. Проверка
- 16. Метод замены переменной Ввести новую переменную Решить уравнение, отбросить посторонние корни Вернуться к первоначальному неизвестному
- 17. Введение вспомогательной переменной в ряде случаев приводит к упрощению уравнения. Чаще всего в качестве новой переменной
- 18. Пример Пусть тогда исходное уравнение примет вид: У1 = -7, у2 = 6
- 19. Решая уравнение получим: Ответ: х = 3; х = - 4,5
- 20. В некоторых случаях можно сделать вывод о решении иррационального уравнения, не прибегая к преобразованиям. Например, уравнения
- 21. Метод пристального взгляда Этот метод основан на следующем теоретическом положении: “Если функция возрастает в области определения
- 22. Пример 1 Наличие радикалов четной степени говорит о том, что подкоренные выражения должны быть неотрицательными. Поэтому
- 23. Пример 2 Рассмотрим функцию Найдем область определения данной функции: Данная функция является монотонно возрастающей.
- 24. Для эта функция будет принимать наименьшее значение при , а далее только возрастать. Число 5 принадлежит
- 25. Решение упражнений № 417 (а, б), 418 (а, б), № 419 (а, б), 422 (а, б)
- 27. Скачать презентацию












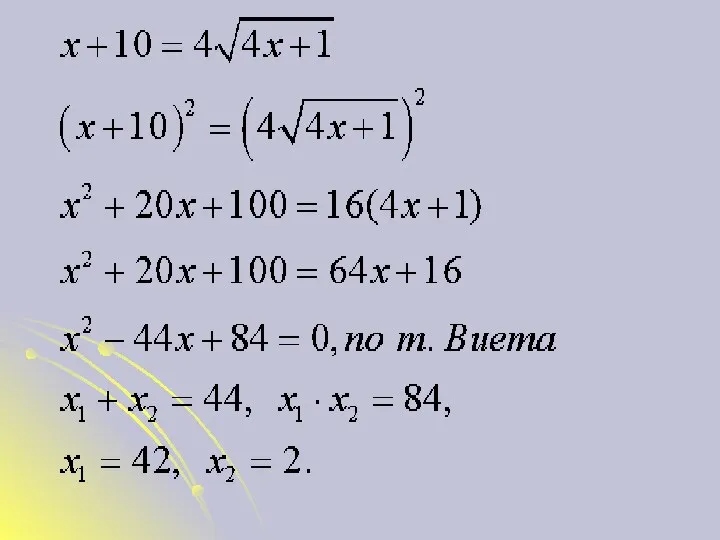











 Леонардо Да Винчи 1452 – 1519
Леонардо Да Винчи 1452 – 1519 Опционное оборудование. Защита кабины оператора
Опционное оборудование. Защита кабины оператора Многопартийность и политические системы
Многопартийность и политические системы Қазақтың сүт өнімдері
Қазақтың сүт өнімдері Авторская модель эффектного и эффективного урока Мацкевич Дмитрий Геннадьевич учитель математики высшей категории УО «Брасла
Авторская модель эффектного и эффективного урока Мацкевич Дмитрий Геннадьевич учитель математики высшей категории УО «Брасла Графическое решение неравенств - презентация по Алгебре
Графическое решение неравенств - презентация по Алгебре Аутсорсинг & аутстаффинг
Аутсорсинг & аутстаффинг Строительные рабочие, организация труда, заработная плата. Система оплаты труда
Строительные рабочие, организация труда, заработная плата. Система оплаты труда Электростатическое поле в диэлектриках
Электростатическое поле в диэлектриках  Имидж гостиничного предприятия (планирование, формирование, продвижение)
Имидж гостиничного предприятия (планирование, формирование, продвижение) Развитие интеллектуальных способностей учащихся через формирование информационно-коммуникативной компетенции в процессе учебн
Развитие интеллектуальных способностей учащихся через формирование информационно-коммуникативной компетенции в процессе учебн Презентация Юридическая ответственность по таможенному праву
Презентация Юридическая ответственность по таможенному праву  Хвойные деревья Томской области
Хвойные деревья Томской области Такие простые и сложные предложения - презентация для начальной школы
Такие простые и сложные предложения - презентация для начальной школы Подготовка к ЕГЭ и предметным олимпиадам Создание и использование тренажеров
Подготовка к ЕГЭ и предметным олимпиадам Создание и использование тренажеров  Микрокомпьютер. Персональные компьютеры
Микрокомпьютер. Персональные компьютеры Кровь
Кровь Климатообразование
Климатообразование Феминизм Подготовили Каграманов Дмитрий и Посаднев Денис
Феминизм Подготовили Каграманов Дмитрий и Посаднев Денис  Образование- путь к успеху. Будущее России за профессионалами во всём
Образование- путь к успеху. Будущее России за профессионалами во всём РЕШАЕМ ТЕСТ А 1 – А 25 Вариант 2 (ЕГЭ-2010. Тренировочные упражнения)
РЕШАЕМ ТЕСТ А 1 – А 25 Вариант 2 (ЕГЭ-2010. Тренировочные упражнения) Циклотрон
Циклотрон  Способ крепления балки штырем для фиксации балки в креплении
Способ крепления балки штырем для фиксации балки в креплении Плоскостные элементы благоустройства территории. Дорожки и площадки
Плоскостные элементы благоустройства территории. Дорожки и площадки Понятие банковского права
Понятие банковского права Органы полиции России во второй половине 19 в. Правоохранительные органы
Органы полиции России во второй половине 19 в. Правоохранительные органы  Алмазы
Алмазы  Нанотехнологии вокруг нас
Нанотехнологии вокруг нас