Содержание
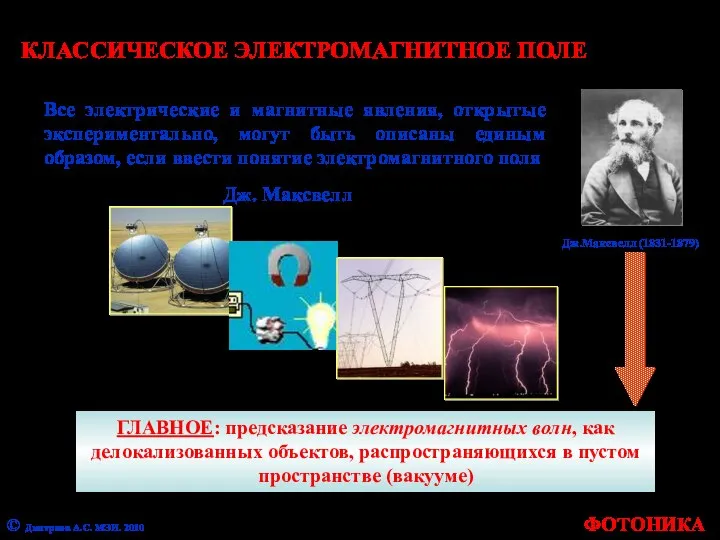
- 2. ФОТОНИКА КЛАССИЧЕСКОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ ГЛАВНОЕ: предсказание электромагнитных волн, как делокализованных объектов, распространяющихся в пустом пространстве (вакууме)
- 3. Что нам уже известно: существуют два вида механики для объектов: классическая механика – описывает точечные объекты,
- 4. Однако, известны и другие объекты природы – например, гидродинамические поля, которые определяют непрерывное изменение в пространстве
- 5. Пусть во всем пространстве имеется векторное поле: Математическое отступление Пусть имеются две интегральных характеристики этого поля
- 6. На основании теоремы Стокса, имеем: где - известная векторная функция координат Оператор набла Способы интегрирования ФОТОНИКА
- 7. В гауссовской системе единиц (CGS) 1.2. ЭЛЕКТРОДИНАМИЧЕСКИЕ УРАВНЕНИЯ МАКСВЕЛЛА (в вакууме) В системе СИ (МКСА) Соотношения
- 8. Закон Кулона: Закон Ампера: © Дмитриев А.С. МЭИ. 2007 А.М.Ампер 1775 - 1836 Ш.О.Кулон 1736-1806 ФОТОНИКА
- 9. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 1.2.1. Другое представление электромагнитного поля - потенциалы Вернемся к уравнениям
- 10. ФОТОНИКА Таким образом, в отличие от электростатики, вектор электрического поля уже не может быть представлен в
- 11. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 Поскольку вектор полностью определяется своими div и rot, необходимо найти
- 12. ФОТОНИКА Информация к размышлению Уравнение типа называется в математической физике уравнением Даламбера, решение которого можно получить
- 13. ФОТОНИКА 1.2.2. Закон сохранения энергии электромагнитного поля Пусть в некоторой области имеются поля, заряды и токи
- 14. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 Таким образом Изменение энергии ЭМ поля со временем в некотором
- 15. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 Замечание Величина не есть потенциальная энергия системы взаимодействующих частиц: плотность
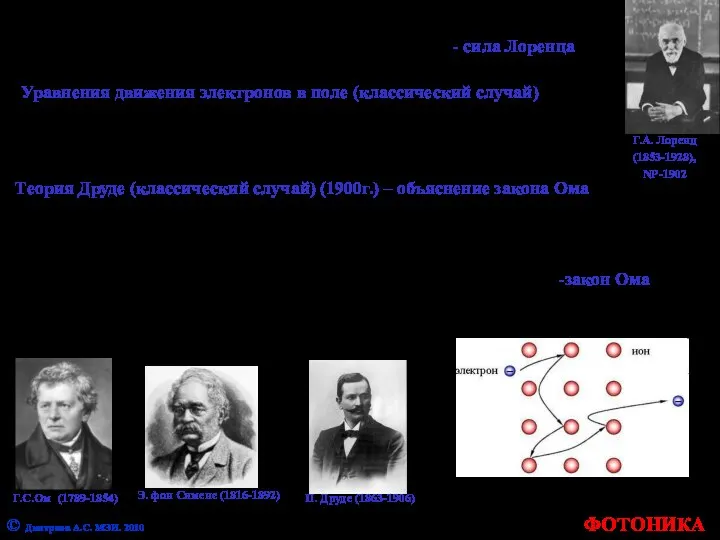
- 16. ФОТОНИКА © Дмитриев А.С. МЭИ. 2010 Г.А. Лоренц (1853-1928), NP-1902 - сила Лоренца Уравнения движения электронов
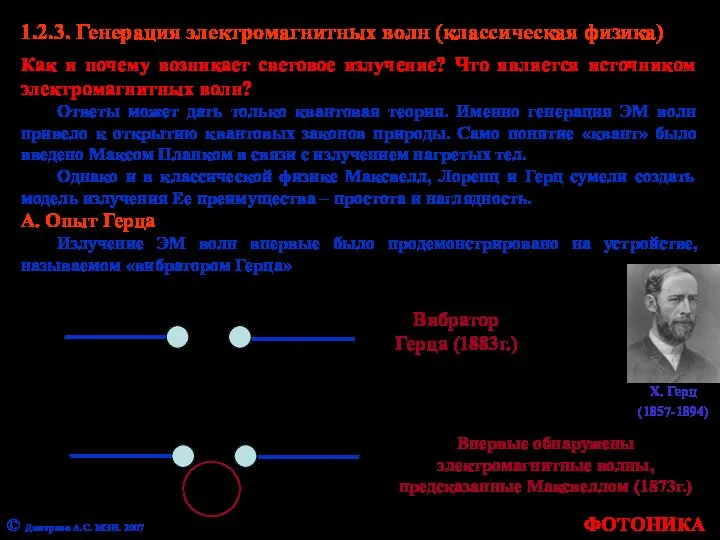
- 17. 1.2.3. Генерация электромагнитных волн (классическая физика) Как и почему возникает световое излучение? Что является источником электромагнитных
- 18. Частота электромагнитных колебаний, зарегистрированная Герцем, составляла 107-108 Гц. Частота видимого света на много порядков выше –
- 19. Продольная и поперечная компоненты электрического поля есть a – ускорение заряда q, с –скорость света, θ
- 20. Вектор дипольного момента есть: В. Гармонические колебания диполя в одномерном случае Пусть дипольный момент совершает гармонические
- 21. Интенсивность излучения есть Полная мощность излучения диполя есть суммарная мощность излучения во всех направлениях. Для этого
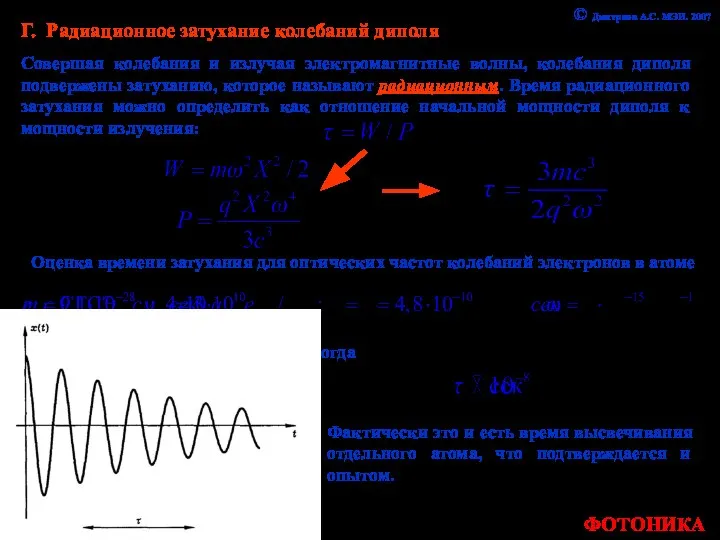
- 22. Г. Радиационное затухание колебаний диполя Совершая колебания и излучая электромагнитные волны, колебания диполя подвержены затуханию, которое
- 23. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 1.3. РАСПРОСТРАНЕНИЕ ЭМ ПОЛЯ В ВАКУУМЕ ГЕНЕРАЦИЯ ЭМ ПОЛЯ РАСПРОСТРАНЕНИЕ
- 24. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 Если нет токов, то уравнение для вектора-потенциала (см. выше) есть
- 25. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 Решение последнего уравнения есть Физический смысл этого решения следующий. Если,
- 26. ФОТОНИКА Откуда единичный вектор вдоль направления распространения волны. Подставляя первое уравнение во второе, получим - электрическое
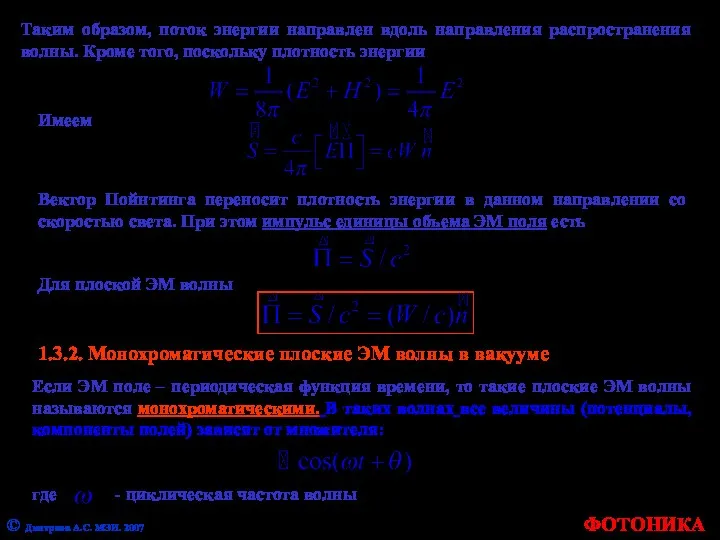
- 27. ФОТОНИКА Таким образом, поток энергии направлен вдоль направления распространения волны. Кроме того, поскольку плотность энергии Имеем
- 28. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 Для монохроматической волны производная по времени есть Для монохроматической плоской
- 29. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 Тогда можно записать периодическую функцию через комплексное представление - некоторый
- 30. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 1.3.3. Поляризация монохроматических плоских ЭМ волн Теперь необходимо понять, как
- 31. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 Из соотношений следует, что Последнее соотношение – уравнение для эллипса.
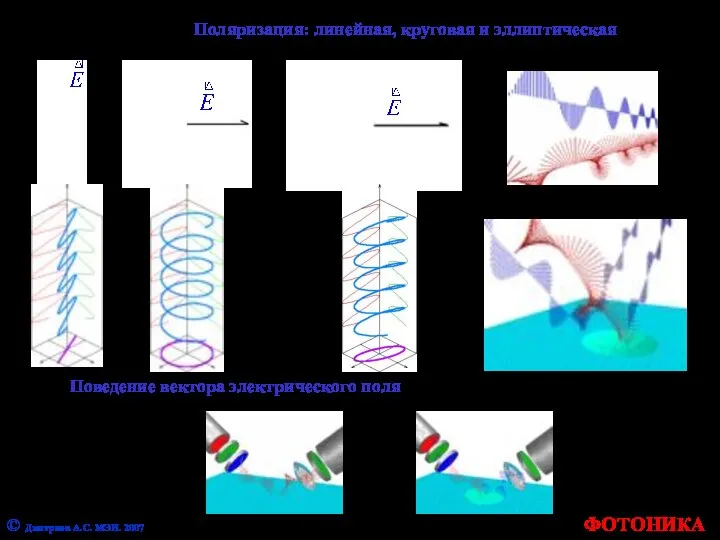
- 32. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 Поляризация: линейная, круговая и эллиптическая Поведение вектора электрического поля
- 33. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 1.3.4. Немонохроматическое ЭМ поле. Естественная поляризация В плоской монохроматической волне
- 34. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 1.3.5. Источники ЭМ поля НЕЛАЗЕРНЫЕ Термические – полихроматические, пространственно некогерентные;
- 35. 1.4. ИЗЛУЧЕНИЕ АНСАМБЛЯ ДИПОЛЕЙ Перейдем от динамики одного осциллятора к к ансамблю таких осцилляторов. Главная проблема
- 36. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 Поскольку фазы осцилляторов распределены равномерно, то Следовательно Итак, вследствие хаотическое
- 37. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 Мощность излучение ансамбля равна сумме средних мощностей отдельных осцилляторов Кроме
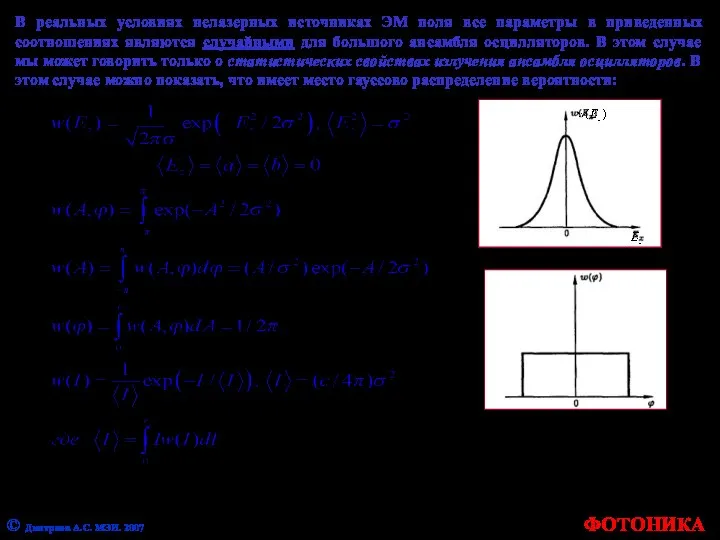
- 38. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 В реальных условиях нелазерных источниках ЭМ поля все параметры в
- 39. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 напряженность поля – гауссово распределение, огибающая - распределение Рэлея, фаза
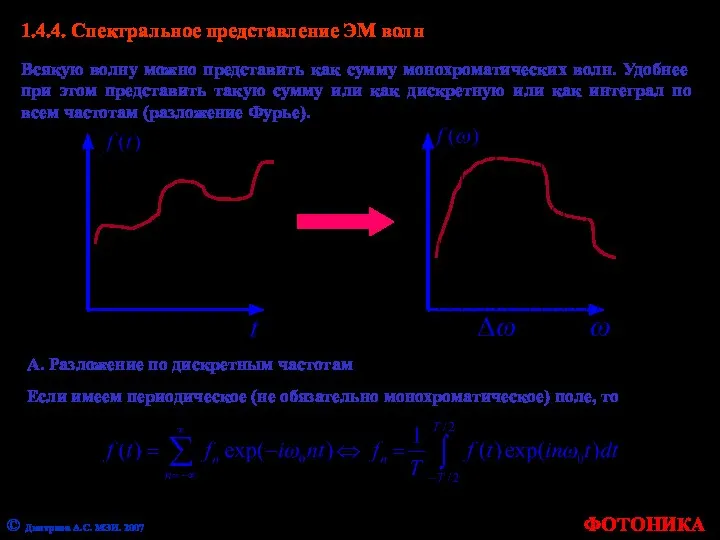
- 40. ФОТОНИКА © Дмитриев А.С. МЭИ. 2007 1.4.4. Спектральное представление ЭМ волн Всякую волну можно представить как
- 42. Скачать презентацию































 Сыры
Сыры Валютное регулирование и валютный контроль
Валютное регулирование и валютный контроль  Расход газа в горизонтальном и рельефном газопроводе
Расход газа в горизонтальном и рельефном газопроводе Искусственное вскармливание
Искусственное вскармливание  Изучение товарных знаков торговых организаций, расположенных в мкр. Левобережный г. Тула
Изучение товарных знаков торговых организаций, расположенных в мкр. Левобережный г. Тула Поиск максимума. Схема алгоритма
Поиск максимума. Схема алгоритма Интернет-маркетинг, как составляющая электронной коммерции
Интернет-маркетинг, как составляющая электронной коммерции Проект музей путешествий
Проект музей путешествий  Анализ деятельности Рекламного Агентства «INFINITI
Анализ деятельности Рекламного Агентства «INFINITI Функционально-ориентированная организация
Функционально-ориентированная организация Гуманитарный идеал научности в менеджменте
Гуманитарный идеал научности в менеджменте  Предмет и задачи культурологии как науки
Предмет и задачи культурологии как науки Испания
Испания  Понятие информации
Понятие информации  Государственная программа «Внешнеполитическая деятельность»
Государственная программа «Внешнеполитическая деятельность» 7 wonders
7 wonders Көшбасшы және көшбасшылық
Көшбасшы және көшбасшылық Квантовые алгоритмы Монте-Карло в непрерывном времени Представление взаимодействия. Общая формулировка CTWL-алгоритма. Процедуры о
Квантовые алгоритмы Монте-Карло в непрерывном времени Представление взаимодействия. Общая формулировка CTWL-алгоритма. Процедуры о Deutscher Rap
Deutscher Rap Экономика информации и неопределенности
Экономика информации и неопределенности Думаете о будущем? Образование в Европе
Думаете о будущем? Образование в Европе Алгоритмические структуры
Алгоритмические структуры Закрытие механические передачи
Закрытие механические передачи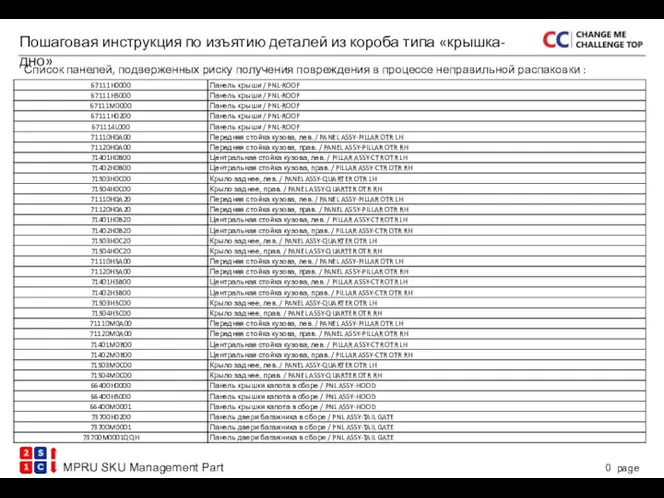 Пошаговая инструкция по изъятию деталей из короба типа «крышка-дно»
Пошаговая инструкция по изъятию деталей из короба типа «крышка-дно» Методологии разработки по MSF, RUP, XP
Методологии разработки по MSF, RUP, XP Федеральный закон "О государственной поддержке кинематографии Российской Федерации" N 126-ФЗ
Федеральный закон "О государственной поддержке кинематографии Российской Федерации" N 126-ФЗ Осенний пейзаж
Осенний пейзаж My sport idol is Alexei Nemov
My sport idol is Alexei Nemov