КЛАССИЧЕСКАЯ ТЕОРИЯ ОПТИМИЗАЦИИ

Сентябрь 3, 2022

Главная
Алгебра
КЛАССИЧЕСКАЯ ТЕОРИЯ ОПТИМИЗАЦИИ

Содержание

2. 10.1. ВВЕДЕНИЕ В классической теории оптимизации для нахождения точек максимума и минимума (экстремальных точек) функций в
3. 10.2. ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ БЕЗ ОГРАНИЧЕНИЙ Экстремальная точка функции f(X) определяет либо ее максимальное, либо минимальное значение.
4. Заметим, что хотя точка х1 является точкой максимума функции f(x) (рис. 8.1), она отличается от остальных
5. Теорема 8.2-1. Необходимым условием того, что точка Х0 является экстремальной точкой функции f(X), является равенство ∇f(X0)
6. Теорема 8.2-2. Для того чтобы стационарная точка Х0 была экстремальной, достаточно, чтобы матрица Гессе Н в
7. Пример 8.2-1 Рассмотрим функцию f(x1, x2, x3) = x1 + 2x3 + x2x3 – x12 –
8. Пример 8.2-2 Рассмотрим функцию f(x1, x2) = 8x1x2 + 3x22. необходимые условия экстремума для которой принимают
9. Теорема 8.2-3. Если в стационарной точке у0 функции f(y) первые (п – 1) ее производных равны
10. Метод Ньютона - Рафсона В общем случае использование необходимого условия экстремума ∇f(X0) = 0 для нахождения
11. Геометрическая интерпретация данного метода для функции одной переменной f(x) приведена на рис. 8.3. Связь между точками
12. 10.3. Задачи на экстремум при наличии ограничений В настоящем разделе рассматриваются задачи поиска экстремумов непрерывных функций
13. Для пояснения изложенной идеи рассмотрим функцию f(x1, x2), график которой представлен на рис. 8.4. Предположим, что
14. Рис. 8.4 При т > п по меньшей мере т – п уравнений системы являются избыточными.
15. Матрица Jm×m называется матрицей Якоби, а Cm×(n–m) — матрицей управления. Матрица Якоби J предполагается невырожденной. Это
16. Достаточные условия экстремума в стационарной точке аналогичны изложенным в разделе 8.2. В этом случае элементы матрицы
17. Оценка приращения ∂c f окрестности допустимой точки Х0 = (1, 2, 3), вызванного малым изменением ∂x2
18. Данный пример иллюстрирует процедуру использования метода приведенного градиента. Рассмотрим задачу Минимизировать f(X) = x12 + x22
19. Далее устанавливаем тип полученной стационарной точки путем проверки выполнения достаточных условий экстремума. Так как x3 —
20. Использование описанного метода Якоби в общем случае может быть затруднено вычислением обратной матрицы J–1, если количество
21. Следовательно, необходимые условия экстремума принимают вид Аналогично в матричном равенстве (i, j) – й элемент вычисляется
22. Анализ чувствительности с помощью метода Якоби. Метод Якоби можно использовать для анализа чувствительности оптимального значения целевой
23. Пример 8.3-3 Рассмотрим задачу из примера 8.3-2. Оптимальной точкой является X0 = (x10, x20, x30) =
24. Это свидетельствует о том, что изменение ∂g1 = 1 приводит к увеличению значения целевой функции f
25. Решение системы уравнений, состоящей из уравнения ∇c f и ограничений задачи, позволяет определить стационарную точку w1
26. Полученный результат можно проверить графически, используя рис. 8.5. Первое из найденных решений (х1 = 4, х2
27. В точке (3, 0) целевая функция двойственной задачи равна 5u1 + 3u2 = 15 совпадает с
28. МЕТОД МНОЖИТЕЛЕЙ ЛАГРАНЖА. Коэффициенты чувствительности метода Якоби можно использовать для решения задач с ограничениями в виде
29. Уравнения дают необходимые условия для определения стационарных точек функции f(X) при ограничениях g(X) = 0. Достаточные
30. Эти условия являются достаточными для определения экстремальной точки. Другими словами, экстремальной может оказаться стационарная точка, не
31. Решением этой системы являются векторы Х0 = (x1, x2, x3) = (0.81, 0.35, 0.28), λ0 =
32. Пример 8.3-5 Рассмотрим задачу Минимизировать z = x12 + x22 + x32 при ограничении 4x1 +
33. Так как т = 1 и п = 3, то для того, чтобы стационарная точка была
34. Для иллюстрации схемы проверки достаточных условий экстремума, которая использует корни полинома, рассмотрим матрицу В точке (Х0,
35. ОБОБЩЕННЫЙ МЕТОД МНОЖИТЕЛЕЙ ЛАГРАНЖА Предположим, что дана задача, в которой требуется Максимизировать z = f(X) при
36. Шаг 3. Если k = т, вычисления прекращаются: задача не имеет допустимых решений. Иначе необходимо положить
37. Точка безусловного экстремума находится как решение уравнений Отсюда имеем (x1, х2) = (5/2, 1/2). Так как
38. Как следует из описанной вычислительной процедуры, при реализации обобщенного метода множителей Лагранжа на большее, чем получение
39. При ограничениях g(X) ≤ 0 необходимым условием оптимальности в задаче максимизации (минимизации) является неотрицательность (соответственно, неположительность)
40. Из второй группы уравнений следуют такие результаты. 1. Если λi не равняется нулю, то Si2 =
41. Процедура проверки выпуклости или вогнутости некоторой функции является более простой, чем доказательство выпуклости множества допустимых решений
42. Пример 8.3-7 Рассмотрим следующую задачу. Минимизировать f(X) = x12 + x22 + x32 при ограничениях g1(X)
43. Эти условия можно упростить и привести к виду λ1, λ2, λ3, λ4, λ5 ≤ 0, 2x1
45. Скачать презентацию

Слайд 2

10.1. ВВЕДЕНИЕ
В классической теории оптимизации для нахождения точек максимума и

минимума (экстремальных точек) функций в условиях, как отсутствия, так и наличия ограничений на переменные широко используется аппарат дифференциального исчисления. Получаемые при этом методы не всегда оказываются удобными при их численной реализации. Однако соответствующие теоретические результаты лежат в основе большинства алгоритмов решения задач нелинейного программирования.
В этой главе изложены необходимые и достаточные условия существования экстремумов функций при отсутствии ограничений на переменные задачи, методы Якоби и Лагранжа для решения задач с ограничениями на переменные в форме равенств, а также условия Куна – Таккера для задач с ограничениями в виде неравенств.

Слайд 3

10.2. ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ БЕЗ ОГРАНИЧЕНИЙ
Экстремальная точка функции f(X) определяет либо

ее максимальное, либо минимальное значение. С математической точки зрения точка Х0 = (х1, ..., xj, ..., хn) является точкой максимума функции f(X), если неравенство
f(X0 + h) ≤ f(X0)
выполняется для всех h = (h1, ..., hj, ..., hn) таких, что |hj| достаточно малы при всех j. Другими словами, точка Х0 является точкой максимума, если значения функции f в окрестности точки Х0 не превышают f(Х0). Аналогично, точка Х0 является точкой минимума функции f(X), если для определенного выше вектора h имеет место неравенство
f(X0 + h) ≥ f(X0)
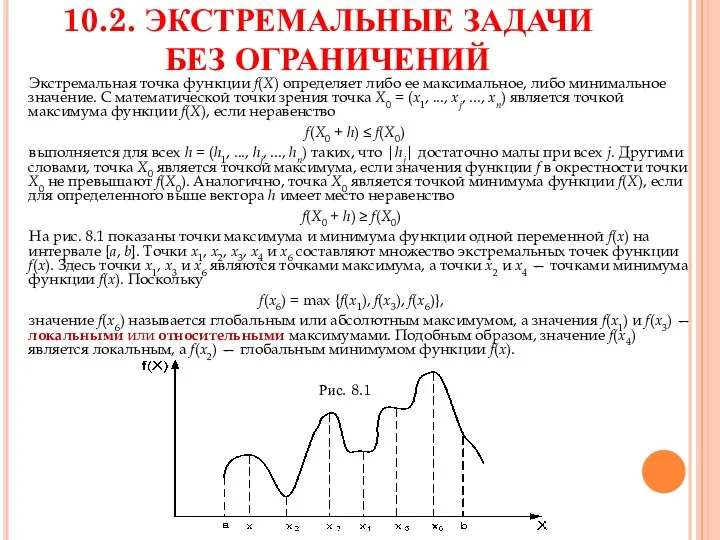
На рис. 8.1 показаны точки максимума и минимума функции одной переменной f(x) на интервале [а, b]. Точки x1, x2, x3, x4 и х6 составляют множество экстремальных точек функции f(x). Здесь точки x1, x3 и х6 являются точками максимума, а точки x2 и x4 — точками минимума функции f(x). Поскольку
f(x6) = max {f(x1), f(x3), f(x6)},
значение f(x6) называется глобальным или абсолютным максимумом, а значения f(x1) и f(x3) — локальными или относительными максимумами. Подобным образом, значение f(x4) является локальным, a f(x2) — глобальным минимумом функции f(x).
Рис. 8.1

Слайд 4

Заметим, что хотя точка х1 является точкой максимума функции f(x)

(рис. 8.1), она отличается от остальных локальных максимумов f(x) тем, что по крайней мере в одной точке ее окрестности значение функции f(x) совпадает c f(x1). Точка х1 по этой причине называется нестрогим (слабым) максимумом функции f(x), в отличие, например, от точки х3, которая является строгим максимумом f(x1). Нестрогий максимум, следовательно, подразумевает наличие (бесконечного количества) различных точек, которым соответствует одно и то же максимальное значение функции. Аналогичные результаты имеют место в точке х4, где функция f(x) имеет нестрогий минимум. В общем случае Х0 является точкой нестрогого максимума функции f(x), если f(X0 + h) ≤ f(X0), и точкой ее строгого максимума, если f(X0 + h) < f(X0), где h — вектор, определенный выше.
На рис. 8.1 легко заметить, что первая производная функции f (тангенс угла наклона касательной к графику функции) равна 0 во всех ее экстремальных точках. Однако это условие выполняется и в точках перегиба и седловых точках функции f таких как точка х5. Если точка, в которой угол наклона касательной к графику функции (градиент функции) равен нулю, не является в то же время точкой экстремума (максимума или минимума), то она автоматически должна быть точкой перегиба или седловой точкой.
Необходимые и достаточные условия существования экстремума
В этом разделе излагаются необходимые и достаточные условия существования экстремумов функции п переменных f(X). При этом предполагается, что первые и вторые частные производные функции f(X) непрерывны в каждой точке X.

Слайд 5

Теорема 8.2-1. Необходимым условием того, что точка Х0 является экстремальной

точкой функции f(X), является равенство
∇f(X0) = 0.
Доказательство. Из теоремы Тейлора следует, что при 0 < θ < 1 имеет место разложение функции f(X)
где h — вектор, определенный выше.
Для достаточно малых значений |hj|остаточный член является величиной порядка hj2. Следовательно,
f(X0 + h) – f(X0) = ∇f(X0)h + O(hj2) ≈ ∇f(X0)h.
Пусть Х0 — точка минимума функции f(X). Докажем от противного, что градиент ∇f(X0) функции f(X) в точке минимума Х0 равен нулю. Пусть это условие не выполняется; тогда для некоторого j должно выполняться условие
Знак hj всегда можно выбрать таким образом, чтобы
Полагая остальные hj равными нулю, из разложения Тейлора получаем неравенство
f(X0 + h) < f(X0).
Этот результат противоречит предположению, что Х0 — точка минимума. Следовательно, величина ∇f(X0) должна равняться нулю. Доказательство для точки максимума проводится аналогично.
Так как необходимое условие выполняется также в точках перегиба и седловых точках, точки, удовлетворяющие уравнению ∇f(X0), называют стационарными. Следующая теорема устанавливает достаточные условия того, что стационарная точка Х0 является экстремальной.

Слайд 6

Теорема 8.2-2. Для того чтобы стационарная точка Х0 была экстремальной,

достаточно, чтобы матрица Гессе Н в точке Х0 была
а)положительно определенной (тогда Х0 — точка минимума);
b)отрицательно определенной (тогда Х0 — точка максимума).
Доказательство. В силу теоремы Тейлора при 0 < θ < 1 имеем
Поскольку Х0 — стационарная точка, в силу теоремы 8.2-1 ∇f(X0) = 0. Таким образом,
Если Х0 — точка минимума, то
f(X0 + h) > f(X0)
для всех ненулевых векторов h. Следовательно, в точке минимума Х0 должно выполняться неравенство
Непрерывность вторых частных производных функции f(X) гарантирует, что
величина имеет один и тот же знак как в точке Х0, так и X0 + θh. Так
как представляет собой квадратичную форму, ее значение (и, следовательно,
) положительно тогда и только тогда, когда — положительно определенная матрица. Это означает, что положительная определенность матрицы Гессе в стационарной точке Х0 является достаточным условием существования в этой точке минимума. Путем аналогичных рассуждений доказывается, что стационарная точка является точкой максимума, если матрица Гессе в этой точке отрицательно определена.

Слайд 7

Пример 8.2-1
Рассмотрим функцию
f(x1, x2, x3) = x1 +

2x3 + x2x3 – x12 – x22 – x32.
Необходимое условие экстремума ∇f(X0) = 0 здесь принимает следующий вид
Решением этой системы уравнений является точка Х0 = (1/2, 2/3, 4/3). Для проверки выполнения условия
достаточности вычислим
Угловые миноры матрицы равны -2, 4 и -6 соответственно. В этом случае является отрицательно определенной матрицей, откуда следует, что точка Х0 = (1/2, 2/3, 4/3) является точкой максимума.
В общем случае, когда матрица является неопределенной, точка Х0 должна быть седловой. Если же матрица оказывается полуопределенной, то соответствующая точка Х0 может как быть, так и не быть экстремальной. При этом формулировка достаточного условия существования экстремума значительно усложняется, ибо для этого необходимо учитывать члены более высоких порядков в разложении Тейлора. (Иллюстрацией вышесказанного в случае функции одной переменной служит теорема 8.2-3.) В некоторых случаях такие сложные процедуры не являются необходимыми, поскольку диагонализация матрицы Н позволяет сделать вывод о наличии или отсутствии экстремума. Проиллюстрируем это следующим примером.

Слайд 8

Пример 8.2-2
Рассмотрим функцию
f(x1, x2) = 8x1x2 + 3x22.

необходимые условия экстремума для которой принимают вид
∇f(x1, x2) = (8x2, 8x1 + 6x2) = (0, 0).
Отсюда следует, что стационарной является точка Х0 = (0, 0). При этом матрица Гессе в точке Х0 имеет вид
и не дает информации о наличии или отсутствии экстремума в рассматриваемой точке. Используя один из методов диагонализации матриц, получаем преобразованную матрицу Гессе
проверка угловых миноров которой свидетельствует, что матрица Н, (и, следовательно, Н) является неопределенной. Если матрица Н приведена к диагональному виду путем преобразования подобия (а это здесь подразумевается), то нет необходимости проверять угловые миноры матрицы Н, так как в этом случае диагональные элементы матрицы Н, являются собственными значениями матрицы H. Поэтому данная матрица будет неопределенной, если диагональные элементы матрицы Н, имеют разные знаки. Следовательно, Х0 — седловая точка.
Применим достаточные условия, полученные в теореме 8.2-2, к функции одной переменной. Пусть у0 — стационарная точка функции f тогда
a) неравенство f ′′(y0) < 0 является достаточным условием существования максимума в точке y0;
b) неравенство f ′′(y0) < 0 является достаточным условием существования минимума в точке у0.
Если же для функции одной переменной f ′′(y0) < 0, то необходимо исследовать производные высших порядков в соответствии со следующей теоремой.

Слайд 9

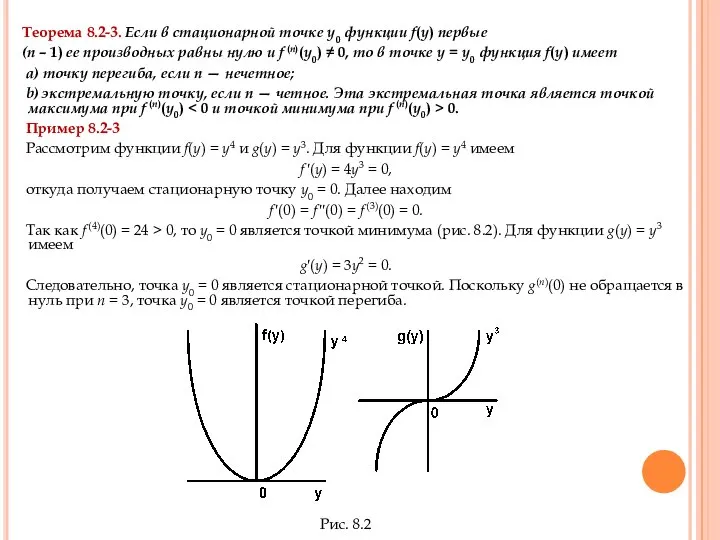
Теорема 8.2-3. Если в стационарной точке у0 функции f(y) первые

(п – 1) ее производных равны нулю и f (n)(y0) ≠ 0, то в точке у = у0 функция f(y) имеет
a) точку перегиба, если п — нечетное;
b) экстремальную точку, если п — четное. Эта экстремальная точка является точкой максимума npu f (n)(y0) < 0 и точкой минимума npu f (n)(y0) > 0.
Пример 8.2-3
Рассмотрим функции f(y) = у4 и g(y) = у3. Для функции f(y) = y4 имеем
f ′(y) = 4у3 = 0,
откуда получаем стационарную точку у0 = 0. Далее находим
f ′(0) = f ′′(0) = f (3)(0) = 0.
Так как f (4)(0) = 24 > 0, то у0 = 0 является точкой минимума (рис. 8.2). Для функции g(y) = у3 имеем
g′(y) = 3у2 = 0.
Следовательно, точка у0 = 0 является стационарной точкой. Поскольку g(n)(0) не обращается в нуль при п = 3, точка у0 = 0 является точкой перегиба.
Рис. 8.2

Слайд 10

Метод Ньютона - Рафсона
В общем случае использование необходимого условия

экстремума ∇f(X0) = 0 для нахождения стационарных точек функции f(Х) может быть сопряжено с трудностями, возникающими при численном решении соответствующей системы уравнений. Метод Ньютона – Рафсона предлагает итерационную процедуру решения системы нелинейных уравнений. Несмотря на то, что данный метод рассматривается в этом разделе именно в указанном контексте, на самом деле он относится к числу градиентных методов численного поиска экстремумов функций при отсутствии ограничений (см. раздел 8.1.2).
Рассмотрим систему уравнений
fi(X) = 0, i = 1, 2, …, m.
Пусть Xk — некоторая фиксированная точка. Используя разложение Тейлора, имеем
fi(X) ≈ fi(Xk) + ∇fi(Xk)(X – Xk), i = 1, 2, …, m.
Следовательно, исходная система уравнений приближенно представима в виде
fi(Xk) + ∇fi(Xk)(X – Xk), i = 1, 2, …, m.
Эти уравнения можно записать в матричной форме:
Ak + Bk(X – Xk) = 0.
Предположим, что векторы fi(X) независимы, тогда матрица Вk является невырожденной. В результате из предыдущего уравнения получим
X = Xk – Bk-1 Ak.
Идея метода Ньютона – Рафсона состоит в следующем. На первом шаге выбирается начальная точка Х0. С помощью полученного уравнения по известной точке Xk можно вычислить координаты новой точки Xk+1. Процесс вычислений завершается в точке Xm, которая считается приближенным решением исходной системы, если Xm ≈ Xm-1.

Слайд 11

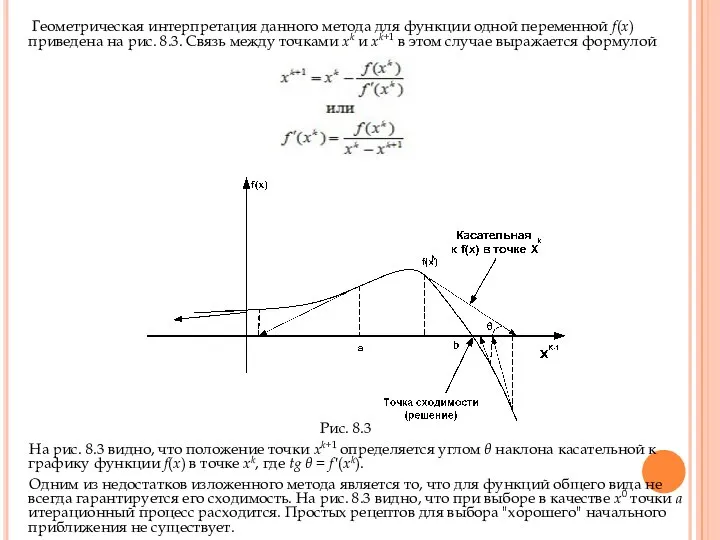
Геометрическая интерпретация данного метода для функции одной переменной f(x) приведена

на рис. 8.3. Связь между точками хk и хk+1 в этом случае выражается формулой
Рис. 8.3
На рис. 8.3 видно, что положение точки хk+1 определяется углом θ наклона касательной к графику функции f(x) в точке хk, где tg θ = f′(xk).
Одним из недостатков изложенного метода является то, что для функций общего вида не всегда гарантируется его сходимость. На рис. 8.3 видно, что при выборе в качестве х0 точки а итерационный процесс расходится. Простых рецептов для выбора "хорошего" начального приближения не существует.

Слайд 12

10.3. Задачи на экстремум при наличии ограничений
В настоящем разделе рассматриваются

задачи поиска экстремумов непрерывных функций при наличии ограничений на переменные. В разделе 8.3.1 рассматривается случай, когда дополнительные ограничения имеют вид равенств, а в разделе 8.3.2 — неравенств.
Ограничения в виде равенств
В данном разделе рассматривается два метода решения оптимизационных задач при наличии ограничений в виде равенств: метод Якоби и метод Лагранжа. Метод Лагранжа можно логически получить из метода Якоби. Эта связь позволяет дать интересную экономическую интерпретацию метода множителей Лагранжа.
МЕТОД ПРИВЕДЕННОГО ГРАДИЕНТА (МЕТОД ЯКОБИ). Рассмотрим задачу
Минимизировать z = f(X)
при ограничениях
g(X) = 0,
где
X = (x1, x2, …, xn),
g = (g1, g2, …, gm).
Функции f(X) и gi(X), i = 1, 2, ..., m, предполагаются дважды непрерывно дифференцируемыми.
Идея использования приведенного градиента заключается в том, чтобы найти замкнутое аналитическое выражение для первых частных производных функции f(X) во всех точках, удовлетворяющих ограничениям g(X) = 0. Соответствующие стационарные точки определяются из условия равенства нулю указанных частных производных. Затем можно использовать достаточные условия, сформулированные в разделе 8.2, для классификации найденных стационарных точек.

Слайд 13

Для пояснения изложенной идеи рассмотрим функцию f(x1, x2), график которой

представлен на рис. 8.4. Предположим, что эту функцию необходимо минимизировать при ограничении
g(x1, x2) = x2 – b = 0,
где b — некоторая константа. На рис. 8.4 видно, что кривая, которая проходит через точки А, В и С, состоит из значений функции f(x1, x2), для которых заданное ограничение выполнено. В соответствии с рассматриваемым методом определяются компоненты приведенного градиента функции f(x1, x2) в каждой точке кривой ABC. Точка B, в которой приведенная производная обращается в нуль, является стационарной для рассматриваемой задачи с ограничением.
Теперь рассмотрим общую математическую формулировку метода. Из теоремы Тейлора следует, что для точек X + ΔX из окрестности точки X имеем
f(X + ΔX) – f(X) = ∇f(X)ΔX + O(Δxj2),
g(X + ΔX) – g(X) = ∇g(X)ΔX + O(Δxj2).
При Δxj → 0 эти уравнения принимают вид
∂f(X) = ∇f(X)∂X,
∂g(X) = ∇g(X)∂X.
Поскольку g(X) = 0, ∂g(X) = 0 в допустимой области. Отсюда следует, что
∂f(X) – ∇f(X)∂X = 0,
∇g(X)∂X = 0.
Как видим, задача сводится к решению
т + 1 уравнений с п + 1 неизвестными,
которыми являются ∂f(X) и ∂X.
Неизвестную величину ∂f(X) можно
определить, как только будет найден
вектор ∂X. Это означает, что, по
существу, имеется т уравнений
с п неизвестными.

Слайд 14

Рис. 8.4
При т > п по меньшей мере т –

п уравнений системы являются избыточными. После устранения избыточности количество независимых уравнений в системе становится равным т (≤п). Если т = п, решением является ∂X = 0. При этом точка X не имеет допустимой окрестности, и, следовательно, пространство решений задачи состоит из единственной точки. Такая ситуация является тривиальной. Ситуацию, когда т < п, рассмотрим подробно.
Пусть
X = (Y, Z),
где
Y = (y1, y2, …, ym) и Z = (z1, z2, …, zn–m)
называются зависимыми и независимыми переменными соответственно. Переписывая градиенты функций f и g в новых обозначениях, получим
∇f(Y, Z) = (∇Y f, ∇Z f),
∇g(Y, Z) = (∇Y g, ∇Z g).
Введем в рассмотрение матрицы

Слайд 15

Матрица Jm×m называется матрицей Якоби, а Cm×(n–m) — матрицей управления.

Матрица Якоби J предполагается невырожденной. Это всегда можно обеспечить, поскольку рассматриваемые т уравнений являются независимыми по определению. Поэтому компоненты вектора Y можно выбрать среди компонентов вектора X таким образом, что матрица J окажется невырожденной.
Исходную систему уравнений с неизвестными ∂f(X) и ∂X можно переписать в следующем виде
∂f(Y, Z) = ∇Y f∂Y + ∇Z f∂X,
J∂Y = –C∂Z.
Так как матрица J невырожденная, существует обратная матрица J–1. Следовательно,
∂Y = – J–1C∂Z.
Подставляя это выражение ∂Y в уравнение для ∂f(Y, Z), можно выразить ∂f через ∂Z в следующем виде
∂f(Y, Z) = (∇Z f – ∇Y fJ–1C)∂Z.
Из этого уравнения получаем формулу для производных функции f по вектору независимых переменных Z
где ∇c f представляет вектор приведенного градиента функции f по Z. Следовательно, вектор ∇c f(Y, Z) должен обращаться в нуль в стационарных точках.

Слайд 16

Достаточные условия экстремума в стационарной точке аналогичны изложенным в разделе

8.2. В этом случае элементы матрицы Гессе будут соответствовать компонентам вектора независимых переменных Z. Между тем элементы матрицы Гессе должны быть приведенными вторыми производными. Чтобы показать, как они вычисляются, положим
∇c f = ∇Z f – WC
Отсюда следует, что i-й строкой приведенной матрицы Гессе является вектор ∂∇c f / ∂ zi Заметим, что W — функция от Y, a Y, в свою очередь, — функция от Z. Следовательно, при вычислении частной производной ∇c f no zi следует применять правило дифференцирования сложной функции, а именно
Пример 8.3-1
Рассмотрим следующую задачу.
f(X) = x12 + 3x22 + 5x1x32,
g1(X) = x1x3 + 2x2 + x22 + 11 = 0,
g2(X) = x12 + 2x1x2 + x32 + 14 = 0.
Известна допустимая точка Х0 = (1, 2, 3). Требуется оценить приращение функции f(= ∂c f) в допустимой окрестности точки Х0. Пусть Y = (x1, x3) и Z = х2. Имеем

Слайд 17

Оценка приращения ∂c f окрестности допустимой точки Х0 = (1, 2,

3), вызванного малым изменением ∂x2 = 0.01, получается следующим образом:
Следовательно, приращение функции f с учетом ограничений равно
Если указана величина изменения ∂x2 независимой переменной х2, то допустимые значения ∂x1 и ∂x3 зависимых переменных x1 и x3 определяются по формуле
∂Y = – J–1C∂Z
При ∂x2 = 0.01 получаем
Чтобы проверить точность полученной выше оценки для ∂c f, можно вычислить значения функции f в точках Х0 и Х0 + ∂X. Получаем
Х0 + ∂X = (1 – 0.0283, 2 + 0.01, 3 + 0.025) = (0.9717, 2.01, 3.025).
Отсюда следует, что
f(X0) = 58, f(X0 + ∂X) = 57.523
или
∂c f = f(X0 + ∂X) – f(X0) = –0.477.
Полученный результат свидетельствует об уменьшении значения функции f по сравнению с вычисленным выше в соответствии с формулой для ∂c f. Это различие между двумя полученными результатами (–0.477 и –0.46) является следствием линейной аппроксимации в окрестности точки Х0. Поэтому приведенная выше формула дает хорошие результаты лишь тогда, когда отклонения от точки Х0 малы.

Слайд 18

Данный пример иллюстрирует процедуру использования метода приведенного градиента. Рассмотрим задачу

Минимизировать f(X) = x12 + x22 + x32,
при ограничениях
g1(X) = x1 + x2 + 3x3 – 2 = 0,
g2(X) = 5x1 + 2x2 + x3 – 5 = 0.
Определяем экстремальные точки целевой функции при наличии ограничений следующим образом. Пусть Y = (x1, x2) и Z = x3. Тогда
Следовательно,
В стационарной точке выполняется равенство ∇c f = 0, которое вместе с ограничениями g1(X) = 0 и g2(X) = 0 определяет искомую стационарную точку (или точки). В данном случае система уравнений
имеет решение X0 ≈ (0.81, 0.35, 0.28).

Слайд 19

Далее устанавливаем тип полученной стационарной точки путем проверки выполнения достаточных

условий экстремума. Так как x3 — независимая переменная, из равенства ∇c f = 0 следует, что
В соответствии с методом Якоби получаем
Теперь путем подстановки находим, что
.
Следовательно, Х0 точка минимума.

Слайд 20

Использование описанного метода Якоби в общем случае может быть затруднено

вычислением обратной матрицы J–1, если количество ограничений задачи велико. Однако этого можно избежать, воспользовавшись правилом Крамера, которое позволяет выразить ∂f через ∂Z. Если zj представляет собой j-ю компоненту вектора Z, и уi – i-я компонента вектора Y, то можно показать, что

Слайд 21

Следовательно, необходимые условия экстремума принимают вид
Аналогично в матричном равенстве
(i, j)

– й элемент вычисляется по формуле
которая представляет собой скорость изменения зависимой переменной уi вызванного изменением независимой переменной zj.
Для получения достаточного условия наличия экстремума i-й элемент вектора W ≡ ∇Y fJ–1 выразим в следующем виде
В качестве иллюстрации использования описанного выше метода установим необходимое условие экстремума в задаче из примера 8.3-2. В этом случае имеем

Слайд 22

Анализ чувствительности с помощью метода Якоби. Метод Якоби можно использовать

для анализа чувствительности оптимального значения целевой функции f к малым изменениям правых частей ограничений оптимизационной задачи. В частности, можно определить, как повлияет на оптимальное значение функции f замена ограничения gi(X) = 0 на gi(X) = ∂gi. Исследование такого типа именуется анализом чувствительности и в некотором смысле аналогично соответствующей процедуре, которая была рассмотрена в линейном программировании. Следует, однако, заметить, что анализ чувствительности в нелинейном программировании приводит к результатам, справедливым лишь в малой окрестности экстремальной точки. Знакомство с такими процедурами будет полезно при изучении метода множителей Лагранжа.
Выше было показано, что
∂f(Y, Z) = ∇Y f ∂Y + ∇Z f ∂Z,
∂g = J∂Y + C∂Z.
Предположим что ∂g ≠ 0, тогда
∂Y = J–1∂g – J–1C∂Z.
Подставляя последнее выражение в уравнение для ∂f(Y, Z), получаем
∂f(Y, Z) = ∇Y f J–1∂g + ∇c f ∂Z,
как было определено ранее. Полученное выражение для ∂f(Y, Z) можно использовать при анализе изменений целевой функции f в малой окрестности допустимой точки Х0, обусловленных малыми изменениями ∂g и ∂Z.
В экстремальной (фактически любой стационарной) точке Х0 = (Y0, Z0) приведенный градиент ∇c f должен быть равен нулю. Следовательно, в точке Х0 имеем
вычисленному в точке Х0. Это значит, что влияние малых изменений ∂g на оптимальное значение функции f можно оценить через скорость изменения функции f по отношению к изменениям g. Эти величины принято называть коэффициентами чувствительности

Слайд 23

Пример 8.3-3
Рассмотрим задачу из примера 8.3-2. Оптимальной точкой является

X0 = (x10, x20, x30) = (0.81, 0.35, 0.28). Так как Y = (x10, x20), то
Следовательно,
Это свидетельствует о том, что изменение ∂g1 = 1 приводит к увеличению значения целевой функции f приблизительно на 0.0867. Аналогично при ∂g2 = 1 имеет место увеличение значения f приблизительно на 0.3067.
Использование метода Якоби в задачах линейного программирования. Рассмотрим задачу линейного программирования.
Максимизировать z = 2x1 + 3x2
при ограничениях
x1 + x2 + x3 = 5,
x1 – x2 + x4 = 3,
x1, x2, x3, x4 ≥ 0.
Для каждого условия неотрицательности xj ≥ 0 введем соответствующую (неотрицательную) дополнительную переменную wj2. Таким образом, xj - wj2 = 0 или xj = wj2. При такой замене условия неотрицательности становятся неявными, и исходная задача принимает вид
Максимизировать z = 2w12 + 3w22
при ограничениях
w12 + w22 + w32 = 5,
w12 – w22 + w42 = 3.

Слайд 24

Это свидетельствует о том, что изменение ∂g1 = 1 приводит

к увеличению значения целевой функции f приблизительно на 0.0867. Аналогично при ∂g2 = 1 имеет место увеличение значения f приблизительно на 0.3067.
Использование метода Якоби в задачах линейного программирования. Рассмотрим задачу линейного программирования.
Максимизировать z = 2x1 + 3x2
при ограничениях
x1 + x2 + x3 = 5,
x1 – x2 + x4 = 3,
x1, x2, x3, x4 ≥ 0.
Для каждого условия неотрицательности xj ≥ 0 введем соответствующую (неотрицательную) дополнительную переменную wj2. Таким образом, xj - wj2 = 0 или xj = wj2. При такой замене условия неотрицательности становятся неявными, и исходная задача принимает вид
Максимизировать z = 2w12 + 3w22
при ограничениях
w12 + w22 + w32 = 5,
w12 – w22 + w42 = 3.
Для метода Якоби положим Y = (w1, w2) и Z = (w3, w4). (В терминологии линейного программирования векторы Y и Z образованы базисными и небазисными переменными соответственно.) Следовательно,

Слайд 25

Решение системы уравнений, состоящей из уравнения ∇c f и ограничений задачи,

позволяет определить стационарную точку w1 = 2, w2 = 1, w3 = 0, w4 = 0. При этом матрица Гессе имеет вид
Поскольку Hc является неопределенной матрицей, стационарная точка не будет точкой максимума.
На самом деле полученный результат не является неожиданным, поскольку (небазисные) переменные w3 и w4 (и, следовательно, х3 и х4) равняются нулю, как и предусмотрено теорией линейного программирования. Следовательно, решение, полученное с помощью метода Якоби, определяет ту или иную крайнюю точку пространства допустимых решений рассматриваемой задачи, которая определяется конкретным выбором векторов Y и Z. При этом найденное решение может, как быть, так и не быть оптимальным. Однако метод Якоби позволяет распознать оптимальное решение задачи путем использования достаточных условий экстремума.
Приведенные рассуждения свидетельствуют о том, что для нахождения оптимального решения задачи линейного программирования необходимо менять конкретный выбор Y и Z, пока не будут выполнены достаточные условия. Пусть, например, Y = (w2, w4) и Z = (w1, w3). Тогда соответствующий приведенный градиент принимает вид
Соответствующая стационарная точка определяется значениями w1 = 0,
w3 = 0, . Так как матрица
является отрицательно определенной, то указанная точка — точка максимума.

Слайд 26

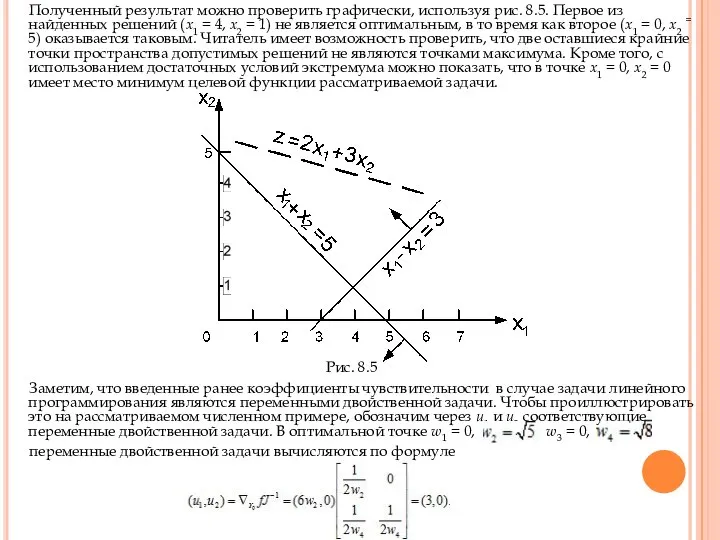
Полученный результат можно проверить графически, используя рис. 8.5. Первое из

найденных решений (х1 = 4, х2 = 1) не является оптимальным, в то время как второе (х1 = 0, х2 = 5) оказывается таковым. Читатель имеет возможность проверить, что две оставшиеся крайние точки пространства допустимых решений не являются точками максимума. Кроме того, с использованием достаточных условий экстремума можно показать, что в точке x1 = 0, х2 = 0 имеет место минимум целевой функции рассматриваемой задачи.
Рис. 8.5
Заметим, что введенные ранее коэффициенты чувствительности в случае задачи линейного программирования являются переменными двойственной задачи. Чтобы проиллюстрировать это на рассматриваемом численном примере, обозначим через u1 и и2 соответствующие переменные двойственной задачи. В оптимальной точке w1 = 0, w3 = 0,
переменные двойственной задачи вычисляются по формуле

Слайд 27

В точке (3, 0) целевая функция двойственной задачи равна 5u1

+ 3u2 = 15 совпадает с оптимальным значением целевой функции прямой задачи. Полученное решение также удовлетворяет ограничениям двойственной задачи, т.е. является допустимым и, следовательно, оптимальным. Это значит, что коэффициенты чувствительности совпадают с переменными двойственной задачи линейного программирования.
Из процедуры применения метода Якоби к решению задач линейного программирования можно сделать несколько общих выводов. Рассмотренный численный пример показывает, что в силу необходимых условий экстремума независимые переменные задачи равны нулю. Достаточные же условия указывают, что матрица Гессе является диагональной. Следовательно, все диагональные элементы этой матрицы должны быть положительными, если в рассматриваемой точке имеет место минимум, и отрицательными — в случае максимума.
Из вышесказанного следует, что необходимое условие экстремума равносильно указанию на то, что оптимальное решение задачи следует искать только среди ее базисных решений. В этом случае в качестве небазисных переменных задачи линейного программирования выступают независимые переменные. Достаточное же условие приводит к выводу, что между диагональными элементами матрицы Гессе и разностями zj – cj, задачи линейного программирования, получаемыми с помощью симплекс-метода, существует строгое соответствие

Слайд 28

МЕТОД МНОЖИТЕЛЕЙ ЛАГРАНЖА.
Коэффициенты чувствительности метода Якоби
можно использовать для

решения задач с ограничениями в виде равенств. Пусть
Следовательно,
∂f – λ∂g = 0.
Это уравнение соответствует необходимым условиям стационарности точек, так как формула для получена с учетом того, что ∇c f = 0. Представленное уравнение можно записать в более удобной форме, если перейти к частным производным по всем переменным xj, что приводит к системе уравнений
Полученные уравнения вместе с ограничениями задачи g = 0 формируют систему, которая позволяет определить допустимые векторы X и λ, удовлетворяющие необходимым условиям стационарности.
Описанная процедура составляет основу метода множителей Лагранжа, который позволяет определять стационарные точки задачи оптимизации с ограничениями в виде равенств. Формально схема этого метода представима в следующем виде. Пусть
L(X, λ) = f(X) – λ∂g(X).
Функция L называется функцией Лагранжа, а параметры X – множителями Лагранжа. Как следует из определения, эти множители имеют тот же смысл, что и коэффициенты чувствительности, фигурирующие в методе Якоби.

Слайд 29

Уравнения
дают необходимые условия для определения стационарных точек функции f(X) при

ограничениях g(X) = 0. Достаточные условия, используемые в методе множителей Лагранжа, будут сформулированы без доказательства. Определим матрицу
Матрица НB называется окаймленной матрицей Гессе.
Пусть имеется стационарная точка (Х0, λ0) функции Лагранжа L(Х, λ) и окаймленная матрица Гессе НB вычислена в точке (Х0, λ0). Тогда Х0 является следующим.
1. Точкой максимума, если, начиная с углового минора порядка 2т + 1, последующие п – т угловых миноров окаймленной матрицы Гессе НB образуют знакопеременный числовой ряд, в котором знак первого члена определяется множителем (–1)m+1.
2. Точкой минимума, если, начиная с углового минора порядка 2т + 1, последующие п – т угловых миноров матрицы НB имеют знаки, определяемые множителем (–1)m.
Эти условия являются достаточными для определения экстремальной точки. Другими словами, экстремальной может оказаться стационарная точка, не удовлетворяющая этим условиям.

Слайд 30

Эти условия являются достаточными для определения экстремальной точки. Другими словами,

экстремальной может оказаться стационарная точка, не удовлетворяющая этим условиям.
Существуют другие условия определения экстремальных точек задачи, которые являются как необходимыми, так и достаточными. Однако их практическое использование часто связано со значительными вычислительными трудностями. Определим матрицу
вычисленную в стационарной точке (Х0, λ0) где μ — неизвестный параметр. Пусть |Δ| – определитель матрицы Δ, тогда все п – т действительных корней ui полинома
|Δ| = 0
должны быть
1. отрицательными, если Х0 — точка максимума,
2. положительными, если Х0 — точка минимума.
Пример 8.3-4
Рассмотрим задачу из примера 8.3-2. Функция Лагранжа имеет вид
L(X, λ) = x12 + x22 + x32 – λ1(x1 + x2 + 3x3 – 2) – λ2(5x1 + 2x2 + x3 – 5).
Необходимые условия экстремума записываются в виде следующей системы уравнений.

Слайд 31

Решением этой системы являются векторы
Х0 = (x1, x2, x3) =

(0.81, 0.35, 0.28),
λ0 = (λ1, λ2) = (0.0867, 0.3067).
В этом решении объединены результаты примеров 8.3-2 и 8.3-3. Как видим, значения множителей Лагранжа λ совпадают со значениями коэффициентов чувствительности, полученными в примере 8.3-3. Это указывает на то, что эти коэффициенты не зависят от выбора вектора зависимых переменных Y при реализации метода Якоби.
Чтобы показать, что найденная точка является точкой минимума, рассмотрим матрицу
Здесь n = 3, m = 2 и n – m = 1. Следовательно, необходимо проверить только определитель матрицы НB, знак которого должен определяться множителем (–1)2 в точке минимума. Так как detHB = 460 > 0, то Х0 является точкой минимума.
При решении систем уравнений, выражающих необходимые условия экстремума, иногда удобно применять метод, который заключается в последовательном выборе числовых значений X, после чего данная система решается относительно X. Процедура повторяется до тех пор, пока вектор X, соответствующий некоторому значению λ, не будет удовлетворять всем ограничениям. В вычислительном плане эта процедура является громоздкой. Можно использовать и другие численные методы решения систем уравнений, например метод Ньютона – Рафсона (раздел 8.2.2).

Слайд 32

Пример 8.3-5
Рассмотрим задачу
Минимизировать z = x12 + x22

+ x32
при ограничении
4x1 + x22 + 2x3 – 14 = 0.
Функция Лагранжа имеет вид
L(X, λ) = x12 + x22 + x32 – λ(4x1 + x22 + 2x3 – 14).
Отсюда получаем необходимые условия экстремума в виде системы
решениями которой являются векторы
(Х0, λ0)1 = (2, 2, 1, 1),
(Х0, λ0)2 = (2, -2, 1, 1),
(Х0, λ0)3 = (2.8, 0, 1.4, 1.4).
Используя достаточные условия, вычислим элементы матрицы

Слайд 33

Так как т = 1 и п = 3, то

для того, чтобы стационарная точка была точкой минимума, знак последних 3 – 1 = 2 угловых миноров должен определяться знаком множителя (–1)m = –1. Таким образом, в точке (Х0, λ0)1 = (2, 2, 1, 1) имеем
Отсюда следует, что (X0)1 и (Х0)2 – точки минимума. Тот факт, что в точке (Х0)3 не удовлетворяются достаточные условия максимума или минимума, не означает, что эта точка не является экстремальной. Это следствие того, что используемые условия являются лишь достаточными.

Слайд 34

Для иллюстрации схемы проверки достаточных условий экстремума, которая использует корни

полинома, рассмотрим матрицу
В точке (Х0, λ0)1 = (2, 2, 1, 1) имеем
|Δ| = 9μ2 – 26μ + 16 = 0,
откуда получаем μ = 2 и μ = 8/9. Так как все μ > 0, то (X0)1 = (2, 2, 1) — точка минимума. В точке (Х0, λ0)2 = (2, -2, 1, 1)
|Δ| = 9μ2 – 26μ + 16 = 0,
что совпадает с рассмотренным выше случаем. Следовательно, (Х0)2 = (2, -2, 1) является точкой минимума. Наконец, в точке (Х0, λ0)3 = (2.8, 0, 1.4, 1.4)
|Δ| = 5μ2 – 6μ + 8 = 0,
откуда получаем μ = 2 и μ = -0.8, что свидетельствует о том, что точка (Х0)3 = (2.8, 0, 1.4) не является экстремальной.
Ограничения в виде неравенств
В данном разделе показано, как метод множителей Лагранжа можно обобщить на случай задачи с ограничениями в виде неравенств. Основную часть раздела составляет вывод условий Куна – Таккера, которые играют важную роль в нелинейном программировании.

Слайд 35

ОБОБЩЕННЫЙ МЕТОД МНОЖИТЕЛЕЙ ЛАГРАНЖА
Предположим, что дана задача, в которой

требуется
Максимизировать z = f(X)
при ограничениях
gi(X) ≤ 0, i = 1, 2, …, m,
Если в рассматриваемой задаче имеются условия неотрицательности переменных X ≥ 0, то предполагается, что они включены в указанные т ограничений.
Основная идея обобщенного метода множителей Лагранжа состоит в том, что если точка безусловного оптимума функции f(X) не удовлетворяет всем ограничениям задачи, то оптимальное решение задачи с ограничениями должно достигаться в граничной точке области допустимых решений. Следовательно, одно или несколько из т ограничений задачи должны выполняться как равенства. Поэтому вычислительная процедура обобщенного метода множителей Лагранжа включает следующие шаги.
Шаг 1. Решается задача без учета ограничений
Максимизировать z = f(X).
Если полученное оптимальное решение удовлетворяет всем ограничениям задачи, вычисления заканчиваются, так как все ограничения являются избыточными. Иначе следует положить k = 1 и перейти к шагу 2.
Шаг 2. Активизируются любые k ограничений задачи (т.е. преобразовываются в равенства) и оптимизируется функция f(X) при наличии k ограничений методом множителей Лагранжа. Если оптимальное решение этой задачи является допустимым по отношению к остальным ограничениям исходной задачи, вычисления заканчиваются: полученная точка является локальным оптимумом. Локальный оптимум определяется из множества оптимумов, полученных в результате оптимизации целевой функции f(Х) при учете всех комбинаций из k ограничений-равенств, k = 1, 2, ..., m. Иначе нужно сделать активными другие k ограничений исходной задачи и повторить данный шаг. Если все подмножества, состоящие из k активных ограничений, не приводят к допустимому решению, следует перейти к шагу 3.

Слайд 36

Шаг 3. Если k = т, вычисления прекращаются: задача не

имеет допустимых решений. Иначе необходимо положить k = k + 1 и перейти к шагу 2.
В описанной вычислительной процедуре часто игнорируется то важное обстоятельство, что она не гарантирует получения глобального оптимума даже в тех случаях, когда задача имеет единственное оптимальное решение. Другим важным моментом является ошибочность интуитивного представления, что если р < q, то оптимальное значение целевой функции f(X) при р ограничениях – равенствах всегда лучше, чем при q ограничениях-равенствах. В общем случае это имеет место лишь в том случае, когда набор из q ограничений является подмножеством набора из р ограничений. Рассматриваемый ниже пример служит иллюстрацией сказанного.
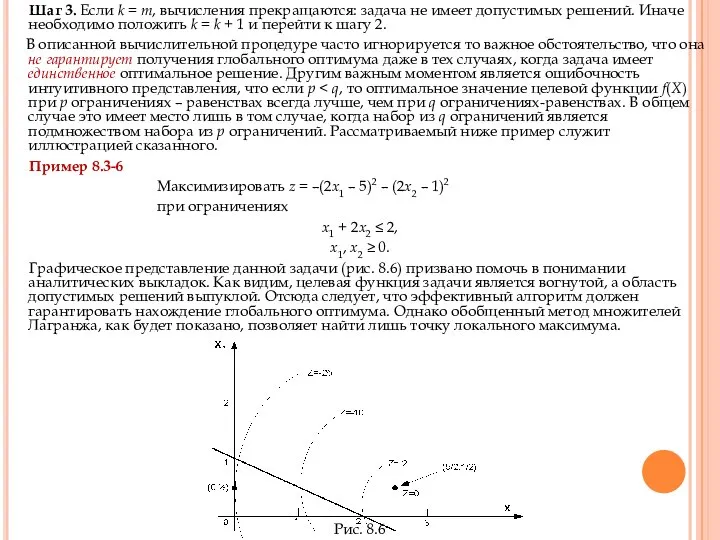
Пример 8.3-6
Максимизировать z = –(2x1 – 5)2 – (2x2 – 1)2
при ограничениях
х1 + 2х2 ≤ 2,
х1, х2 ≥ 0.
Графическое представление данной задачи (рис. 8.6) призвано помочь в понимании аналитических выкладок. Как видим, целевая функция задачи является вогнутой, а область допустимых решений выпуклой. Отсюда следует, что эффективный алгоритм должен гарантировать нахождение глобального оптимума. Однако обобщенный метод множителей Лагранжа, как будет показано, позволяет найти лишь точку локального максимума.
Рис. 8.6

Слайд 37

Точка безусловного экстремума находится как решение уравнений
Отсюда имеем (x1, х2)

= (5/2, 1/2). Так как это решение не удовлетворяет условию х1 + 2х2 ≤ 2, ограничения поочередно активизируются. Рассмотрим ограничение x1 = 0. Функция Лагранжа в этом случае примет вид
L(x1, x2, λ) = –(2x1 – 5)2 – (2x2 – 1)2 – λx1.
Следовательно,
Решением этой системы будет точка (х1, х2) = (0, 1/2), которая является точкой максимума, в чем можно убедиться, используя достаточное условие. Поскольку эта точка удовлетворяет остальным ограничениям исходной задачи, вычислительная процедура завершается: (х1, х2) = (0, 1/2) — точка локального максимума задачи. (Заметим, что если поочередно активизировать оставшиеся ограничения задачи х2 ≥ 0 и х1 + 2х2 ≤ 2, то получаются недопустимые решения.) Оптимальное значение целевой функции z =-25.
Как видно из рис. 8.6, допустимому решению (х1, х2) = (2, 0) рассматриваемой задачи, которое определяется точкой пересечения двух прямых х2 = 0 и х1 + 2х2 = 2, соответствует значение целевой функции z = –2. Оно лучше значения функции z, которое получено с учетом одного активного ограничения.

Слайд 38

Как следует из описанной вычислительной процедуры, при реализации обобщенного метода

множителей Лагранжа на большее, чем получение приемлемого допустимого решения задачи, не следует рассчитывать. Особенно это проявляется тогда, когда целевая функция задачи не является одновершинной. Если в оптимизационной задаче имеется единственный (глобальный) условный экстремум (как в примере 8.3-6), то для его нахождения можно использовать откорректированный обобщенный метод множителей Лагранжа. Для этого необходимо провести сравнение безусловного оптимума и условных экстремумов, полученных с учетом всех возможных наборов активных ограничений, т.е. когда сначала отдельные ограничения делаются активными поочередно, затем рассматриваются пары активных ограничений и так до тех пор, пока все т ограничений рассматриваемой задачи не станут активными. Наилучший из всех таких допустимых экстремумов является глобальным.
Если эту процедуру применить к решению задачи из примера 8.3-6, то для определения глобального экстремума необходимо решить семь задач. Это свидетельствует о том, что возможности использования обобщенного метода множителей Лагранжа для решения практических задач ограничены.
УСЛОВИЯ КУНА-ТАККЕРА.
Данный раздел посвящен рассмотрению необходимых условий Куна – Таккера, которые позволяют определять стационарные точки в задаче нелинейного программирования с ограничениями в виде неравенств. В основу изложения положен метод множителей Лагранжа. Эти условия являются также и достаточными, если выполняются определенные правила, которые описаны ниже.
Рассмотрим следующую задачу.
Максимизировать z = f(X)
при ограничениях
g(X) ≤ 0.
Ограничения-неравенства можно преобразовать в равенства с помощью неотрицательных дополнительных переменных. Пусть Si2 (≥ 0) — дополнительная переменная, которая прибавляется к левой части i-го ограничения gi(X) ≤ 0 и пусть
где m — общее количество ограничений-неравенств. Следовательно, функция Лагранжа записывается в виде

Слайд 39

При ограничениях g(X) ≤ 0 необходимым условием оптимальности в задаче

максимизации (минимизации) является неотрицательность (соответственно, неположительность) множителей λ. Приведем обоснование этого. Рассмотрим задачу максимизации. Так как множители λ выражают скорость изменения целевой функции f по отношению к изменениям g, т.е.
то как только правая часть ограничения g(X) ≤ 0 увеличивается и становится больше нуля, область допустимых решений задачи расширяется и, следовательно, оптимальное значение целевой функции не может уменьшиться. Это значит, что λ ≥ 0. Аналогично в случае задачи минимизации при увеличении правой части ограничения оптимальное значение функции f не может увеличиться, откуда следует, что λ ≤ 0. Если же ограничения задачи имеют вид равенств, т.е. g(X) = 0, то компоненты вектора λ по знаку не ограничены.
Указанные выше ограничения на вектор λ должны рассматриваться как часть необходимых условий Куна-Таккера. Теперь получим остальные условия.
Вычисляя частные производные функции L по X, S и λ и приравнивая их к нулю, получаем

Слайд 40

Из второй группы уравнений следуют такие результаты.
1. Если λi

не равняется нулю, то Si2 = 0. Это означает, что соответствующий этому ограничению ресурс является дефицитным и, следовательно, полностью исчерпан (ограничение имеет вид равенства).
2. Если Si2 > 0, то λi = 0. Это значит, что i-й ресурс дефицитным не является и, следовательно, не влияет на значение целевой функции f (т.е. ).
Из второй и третьей групп уравнений следует, что
λi gi(X) = 0, i = 1, 2, …, m,
Полученные условия фактически подтверждают предыдущий результат, ибо если λi > 0, то gi(X) = 0 или S12 = 0. Аналогично при gi(X) < 0, S12 > 0 и, следовательно, λi = 0.
Теперь для задачи максимизации можно сформулировать условия Куна-Таккера, необходимые для того, чтобы векторы Х и λ определяли стационарную точку:
λ ≥ 0,
∇f(X) - λ∇g(X) = 0,
λi gi(X) = 0, i = 1, 2, …, m,
g(X) ≤ 0.
Читатель имеет возможность самостоятельно убедиться, что эти условия применимы также к задаче минимизации, за тем лишь исключением, что вектор λ должен быть неположительным, как это было установлено ранее. Как в случае задачи максимизации, так и задачи минимизации множители Лагранжа, соответствующие ограничениям в виде равенств, по знаку не ограничены.
Достаточность условий Куна—Таккера, Если целевая функция и область допустимых решений рассматриваемой задачи обладают определенными свойствами, связанными с выпуклостью и вогнутостью, то необходимые условия Куна-Таккера являются также достаточными. Упомянутые свойства перечислены в табл. 8.1.

Слайд 41

Процедура проверки выпуклости или вогнутости некоторой функции является более простой,

чем доказательство выпуклости множества допустимых решений экстремальной задачи. Так как выпуклость допустимого множества может быть установлена путем непосредственной проверки выпуклости или вогнутости функций ограничений, по этой причине мы приводим перечень требований, которые легче использовать на практике. Чтобы установить эти требования, рассмотрим задачу нелинейного программирования в общей постановке.
Максимизировать и минимизировать z = f(x)
при ограничениях
gi(x) ≤ 0, i = 1, 2, …, r,
gi(x) ≥ 0, i = r + 1, 2, …, p,
gi(x) = 0, i = p + 1, 2, …, m.
При этом функция Лагранжа имеет вид
где λi — множитель Лагранжа, соответствующий i-му ограничению. Требования, которые устанавливают достаточность условий Куна – Таккера, приведены в табл. 8.2.
В табл. 8.2 представлена лишь часть условий, упомянутых в табл. 8.1. Это связано с тем, что область допустимых решений задачи может быть выпуклой и в то же время функции ограничений, которые ее формируют, не соответствуют требованиям, перечисленным в табл. 8.2. Таблица 8.2
Законность положений табл. 8.2 основана на том, что при сформулированных условиях функция Лагранжа L(X, S, λ) является вогнутой в случае задачи максимизации и выпуклой — в случае задачи минимизации. Это подтверждается тем, что если gi(X) — выпуклая функция, то функция λI gi(X) оказывается выпуклой при λi ≥ 0 и вогнутой — при λi ≤ 0. Аналогичные рассуждения подтверждают все остальные условия. Заметим также, что линейная функция является как выпуклой, так и вогнутой. Наконец, если функция f вогнутая, то функция –f является выпуклой, и наоборот.

Слайд 42

Пример 8.3-7
Рассмотрим следующую задачу.
Минимизировать f(X) = x12 +

x22 + x32
при ограничениях
g1(X) = 2x1 + x2 – 5 ≤ 0,
g2(X) = 2x1 + x2 – 5 ≤ 0,
g3(X) = 1 – x1 ≤ 0,
g4(X) = 2 – x2 ≤ 0,
g5(X) = – x3 ≤ 0.
Поскольку рассматривается задача минимизации, то λ ≤ 0. Поэтому условия Куна – Таккера записываются в следующем виде.
λ1, λ2, λ3, λ4, λ5 ≤ 0,
λ1g1 = λ2g2 = … = λ5g5 = 0,
g(X) ≤ 0.

Слайд 43

Эти условия можно упростить и привести к виду
λ1, λ2, λ3,

λ4, λ5 ≤ 0,
2x1 – 2λ1 – λ2 + λ3 = 0,
2x2 – λ1 + λ4 = 0,
2x3 – λ2 + λ5 = 0,
λ1(2x1 + x2 – 5) = 0,
λ2(x1 + x3 – 2) = 0,
λ3(1 – x1) = 0,
λ4(2 – x2) = 0,
λ5x3 = 0,
2x1 + x2 ≤ 5,
x1 + x3 ≤ 2,
x1 ≥ 1, x2 ≥ 2, x3 ≥ 0,
Отсюда получаем решение: x1 = 1, x2 = 2, x3 = 0, λ1 = λ2 = λ5 = 0, λ3 = –2, λ4 = –4. Поскольку и целевая функция f(X), и область допустимых решений g(X) ≤ 0 являются выпуклыми, функция L(X, S, λ) также должна быть выпуклой, и полученная стационарная точка определяет глобальный минимум задачи. Рассмотренный пример показывает также, что решение системы, порожденной условиями Куна – Таккера, в явной форме может быть затруднительным. Следовательно, для численных расчетов описанная процедура не подходит. Тем не менее, условия Куна – Таккера играют основополагающую роль при рассмотрении алгоритмов решения задач нелинейного программирования в главе 9.

КЛАССИЧЕСКАЯ ТЕОРИЯ ОПТИМИЗАЦИИ

Содержание

10.1. ВВЕДЕНИЕ В классической теории оптимизации для нахождения точек максимума и

10.2. ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ БЕЗ ОГРАНИЧЕНИЙ Экстремальная точка функции f(X) определяет либо