Содержание
- 2. Содержание История исследования (19 столетий ожидания) Коника Экспериментальное доказательство Вездесущий эллипс/применение конических сечений Словарь Список источников
- 3. История исследования (19 столетий молчания) Менехм Евклид Архимед Аполлоний Пергский Ферма Декарт Эйлер
- 4. Менехм (IV в. до н. э.) Впервые конические сечения (10) появились у Менехма (IV в. до
- 5. Евклид (III в. до н. э.) С именем Евклида связывают становление александрийской математики (геометрической алгебры) как
- 6. Архимед (ок. 287–212)) Разработал предвосхитившие интегральное исчисление методы нахождения площадей, поверхностей и объемов различных фигур и
- 7. Архимед (ок. 287–212))
- 8. Аполлоний Пергский (ок. 260–ок. 170) Аполлоний прославился в первую очередь выдающейся работой «Конические сечения» (8 книг),
- 9. Аполлоний Пергский (ок. 260–ок. 170) рис. 9 В работе Аполлония «Конические сечения» восемь книг; до наших
- 10. Аполлоний Пергский (ок. 260–ок. 170) рис. 9
- 11. Аполлоний Пергский (ок. 260–ок. 170) рис. 9 Из других заслуг Аполлония перед наукой стоит отметить, что
- 12. Аполлоний Пергский (ок. 260–ок. 170) рис. 9 Большой интерес представляют не только результаты Аполлония, но и
- 13. Пьер Ферма (1601–1665) рис. 9
- 14. Рене Декарт (1596–1650) рис. 9 «Геометрия» (аналитическая геометрия) получила наибольшую известность. «Геометрия» состоит из трех книг.
- 15. Леонард Эйлер (1707–1783) рис. 9 В 1748 г. Эйлер опубликовал большое сочинение «Введение в анализ бесконечных»
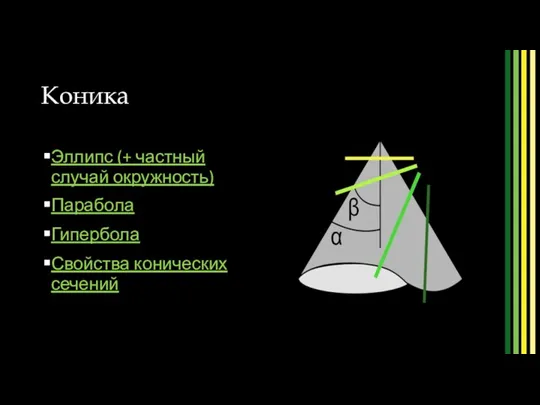
- 16. Коника Эллипс (+ частный случай окружность) Парабола Гипербола Свойства конических сечений
- 17. Эллипс рис. 9
- 18. Эллипс рис. 9
- 19. Парабола рис. 9
- 20. Парабола рис. 9
- 21. Гипербола рис. 9
- 22. Гипербола рис. 9
- 23. Свойства конических сечений рис. 9 Геометрическое место точек плоскости, для каждой из которых отношение расстояния до
- 24. Экспериментальное доказательство Опыт №1 (с вафельным стаканчиком) Опыт №2 (с карманным фонариком) Как начертить эллипс?
- 25. Опыт № 1 рис. 9
- 26. Опыт № 2 рис. 9
- 27. Как начертить эллипс? рис. 9
- 28. Вездесущий эллипс рис. 9
- 29. Словарь
- 30. Словарь
- 31. Словарь
- 32. Словарь
- 33. Список источников Галкин Е. В. Краткая история математики. – М.: АСТ, 2003. – 229с. Карпушина Н.
- 35. Скачать презентацию






























 Даргинцы. История происхождения
Даргинцы. История происхождения Развитие орфографической зоркости у младших школьников
Развитие орфографической зоркости у младших школьников О трояком корне закона непротиворечия Горбатов В.В.
О трояком корне закона непротиворечия Горбатов В.В. Қазақстандағы діни секталар
Қазақстандағы діни секталар Расчет и построение платья полуприлегающего силуэта с вытачками
Расчет и построение платья полуприлегающего силуэта с вытачками Лекция 4
Лекция 4 Тульский Государственный Музей Оружия Составили воспитанники подготовительной группы №6 Ляна Вильк Никита Бабурин Максим Крыл
Тульский Государственный Музей Оружия Составили воспитанники подготовительной группы №6 Ляна Вильк Никита Бабурин Максим Крыл Требования к системе управления ВМФ
Требования к системе управления ВМФ Готов к труду и обороне. Горжусь тобой, Отечество. ГТО - путь к здоровью
Готов к труду и обороне. Горжусь тобой, Отечество. ГТО - путь к здоровью Устойчивость функционирования объектов экономики при ЧС
Устойчивость функционирования объектов экономики при ЧС Что такое кружок "Городец"
Что такое кружок "Городец" Бағдарлама сапасының критерийлері. Диалогтік бағдарламалар. (Тема 4)
Бағдарлама сапасының критерийлері. Диалогтік бағдарламалар. (Тема 4) Измерение напряжений и уровней сигналов
Измерение напряжений и уровней сигналов Групповые переключатели. Реостатный контроллер 1КС.009, реверсивно-тормозной переключатель 1П.004.У2
Групповые переключатели. Реостатный контроллер 1КС.009, реверсивно-тормозной переключатель 1П.004.У2 Артикуляционный отдел
Артикуляционный отдел  Благоустройство общественных территорий г. Кингисеппа
Благоустройство общественных территорий г. Кингисеппа Объектно-ориентированное проектирование ПС (часть 2)
Объектно-ориентированное проектирование ПС (часть 2) Определители и способы их вычисления
Определители и способы их вычисления  Логарифмическая линия в ЕГЭ - 2011
Логарифмическая линия в ЕГЭ - 2011  Социализм. Основные принципы учения
Социализм. Основные принципы учения Киргизия - страна снежных вершин
Киргизия - страна снежных вершин Модели Вселенной, история представлений о вселенной
Модели Вселенной, история представлений о вселенной Микеланджело Меризи да Караваджо(15711610) – итальянский художник
Микеланджело Меризи да Караваджо(15711610) – итальянский художник JavaScript
JavaScript Ғажайып алаң
Ғажайып алаң  Исковые требования. Решение задач
Исковые требования. Решение задач Многоэтажное жилое здание со встроенными помещениями и подземной автостоянкой. Курсовой проект
Многоэтажное жилое здание со встроенными помещениями и подземной автостоянкой. Курсовой проект ЗНО-2015 Особливості проведення
ЗНО-2015 Особливості проведення