Содержание
- 2. Квантовая механика Волновая функция. Уравнение Шредингера Стационарное уравнение Шредингера Квантовая частица в одномерной бесконечно глубокой потенциальной
- 3. Волновая функция В квантовой механике волновой функцией называют волну де Бройля - для свободной частицы Если
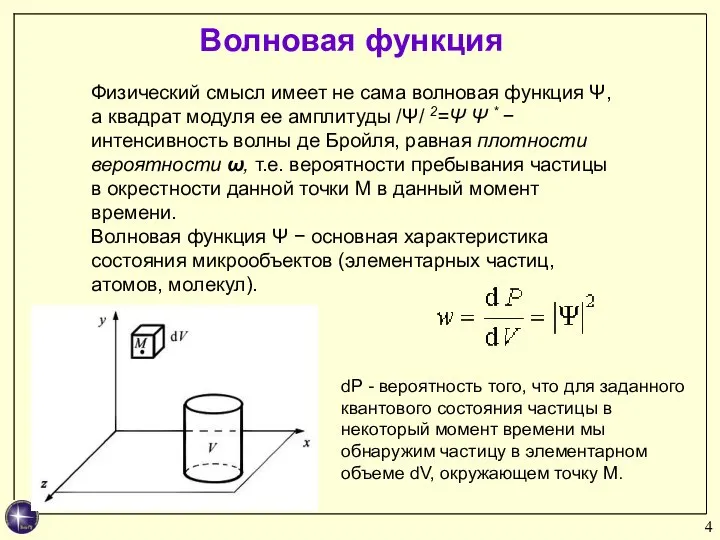
- 4. Волновая функция Физический смысл имеет не сама волновая функция Ψ, а квадрат модуля ее амплитуды /Ψ/
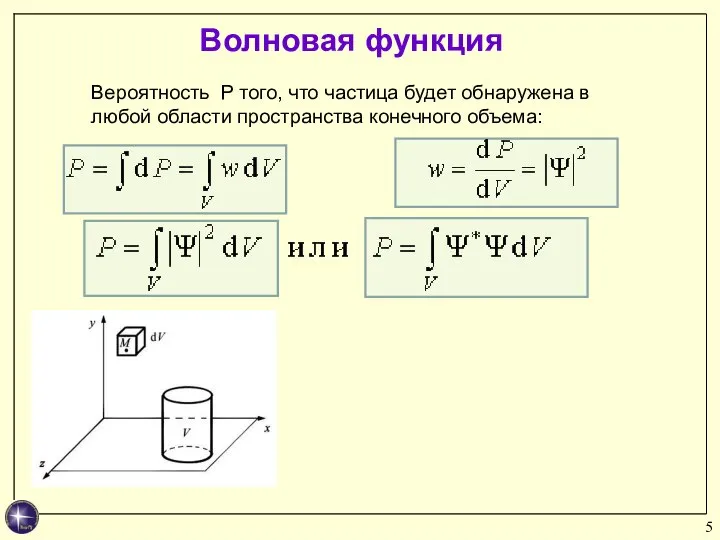
- 5. Волновая функция Вероятность P того, что частица будет обнаружена в любой области пространства конечного объема:
- 6. Уравнение Шредингера 1926 г. Основное уравнение нерелятивистской квантовой механики, справедливо только в случае движения частиц со
- 7. Уравнение Шредингера В общем случае в задачах квантовой механики дифференциальное уравнение Шредингера в частных производных должно
- 8. Уравнение Шредингера Дополнительные условия, накладываемые на функцию Ψ: Ψ − конечная, непрерывная и однозначная; 2) производные
- 9. Уравнение Шредингера. Стационарное решение Если все наблюдаемые физические параметры стационарны, т.е. не зависят от времени, в
- 10. Примеры решения простейших квантово-механических задач 1. Движение свободной частицы Частица движется вдоль оси x с постоянной
- 11. 2. Частица в бесконечно глубокой одномерной потенциальной яме Потенциальная энергия частицы принимает значения: Частица, находящаяся в
- 12. 2. Частица в бесконечно глубокой одномерной потенциальной яме Расстояние между соседними уровнями энергии для больших n
- 13. 2. Частица в бесконечно глубокой одномерной потенциальной яме Из граничных условий (1) α = 0, sin(kl)
- 14. 2. Частица в бесконечно глубокой одномерной потенциальной яме http://www.teachmen.ru/work/lectureSQ/ (2) Коэффициент A находится из условия нормировки
- 15. Подведем итоги: энергия основного состояния частицы не равна нулю; энергия частицы квантована и значение ее пропорционально
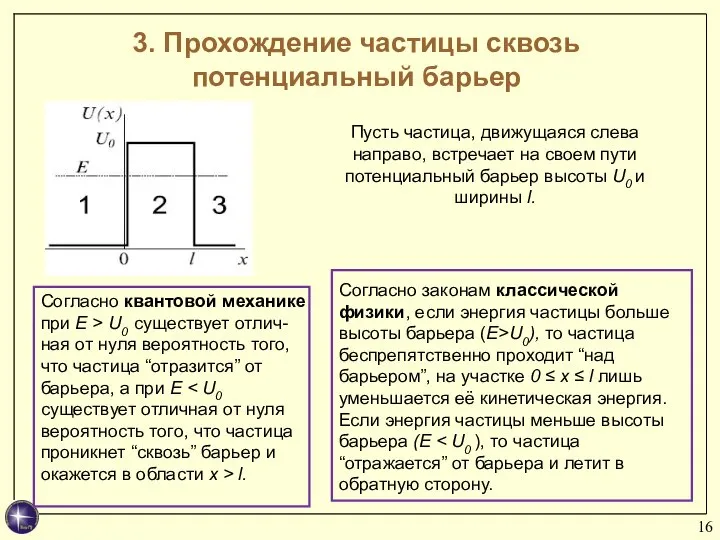
- 16. 3. Прохождение частицы сквозь потенциальный барьер Согласно законам классической физики, если энергия частицы больше высоты барьера
- 17. 3. Прохождение частицы сквозь потенциальный барьер Ограничимся случаем E Решения
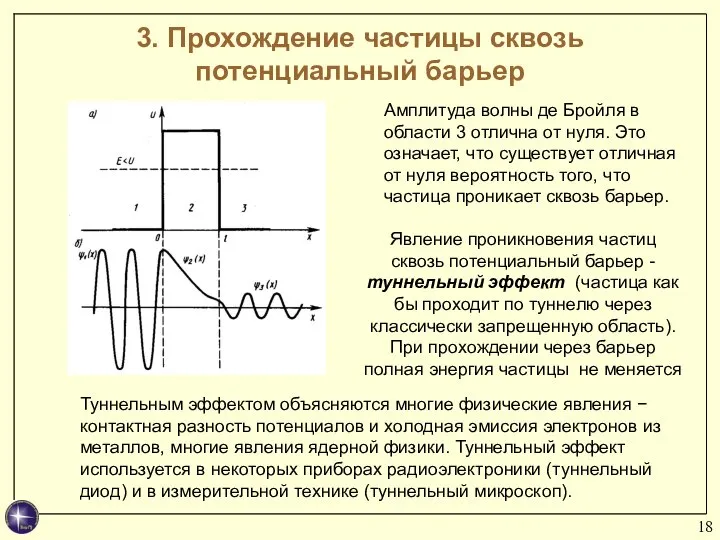
- 18. Амплитуда волны де Бройля в области 3 отлична от нуля. Это означает, что существует отличная от
- 20. Скачать презентацию













 Презентация на тему "Эндокринная регуляция беременности" - скачать презентации по Медицине
Презентация на тему "Эндокринная регуляция беременности" - скачать презентации по Медицине Управление капитальным строительством. (Лекция 11)
Управление капитальным строительством. (Лекция 11) Конструктивные особенности сжатых железобетонных элементов
Конструктивные особенности сжатых железобетонных элементов Портрет в изобразительном искусстве XX века
Портрет в изобразительном искусстве XX века Автомобильдер мен тракторлардың тежеуіш жүйелері
Автомобильдер мен тракторлардың тежеуіш жүйелері Какой вид спорта лучше? Презентацию выполнила Ветринская Е.А. Учитель начальных классов МОУ СОШ №3 п.Никель Мурманской обл.
Какой вид спорта лучше? Презентацию выполнила Ветринская Е.А. Учитель начальных классов МОУ СОШ №3 п.Никель Мурманской обл. Українські меценати. Родина терещенко
Українські меценати. Родина терещенко Вымышленные религии в компьютерных играх
Вымышленные религии в компьютерных играх Христианство. Православие. Часть II. Православный храм - 1
Христианство. Православие. Часть II. Православный храм - 1 Урок по теме «Боги древних славян» 3 класс (Программа «Начальная школа XXI века»)
Урок по теме «Боги древних славян» 3 класс (Программа «Начальная школа XXI века») Урок МХК 9 класс Учитель МХК МОУ СОШ № 4 с. Малые Ягуры Адоньева Д. Н.
Урок МХК 9 класс Учитель МХК МОУ СОШ № 4 с. Малые Ягуры Адоньева Д. Н.  Ансамбль Афинского Акрополя. Греция
Ансамбль Афинского Акрополя. Греция ВЫБОР ТЕРАПЕВТИЧЕСКОЙ ТАКТИКИ ПРИ ХРОНИЧЕСКОЙ БОЛЕЗНИ ПОЧЕК КРАСНОВА Т.Н.
ВЫБОР ТЕРАПЕВТИЧЕСКОЙ ТАКТИКИ ПРИ ХРОНИЧЕСКОЙ БОЛЕЗНИ ПОЧЕК КРАСНОВА Т.Н.  Асинхронные двигатели
Асинхронные двигатели Школа научного менеджмента Ф. Тейлора Петрова М. Зедеев А.
Школа научного менеджмента Ф. Тейлора Петрова М. Зедеев А. Christlich Demokratische Union Deutschlands
Christlich Demokratische Union Deutschlands Судебная риторика: тактика, приемы, особенности
Судебная риторика: тактика, приемы, особенности Радиостанция Баклан 20
Радиостанция Баклан 20 Презентация менежмент ОСОБЕННОСТИ КОМАНД
Презентация менежмент ОСОБЕННОСТИ КОМАНД Pascal Файлы
Pascal Файлы  文化全景练习
文化全景练习 Греция, город Кавала Фестиваль Cosmopolis 18 – 25 июля 2016 года
Греция, город Кавала Фестиваль Cosmopolis 18 – 25 июля 2016 года Ольга Алексеевна Зайцева
Ольга Алексеевна Зайцева Теория видеомонтажа
Теория видеомонтажа Соотношение конституционных положений о свободе предпринимательской и иной экономической деятельности с нормами уголовного зак
Соотношение конституционных положений о свободе предпринимательской и иной экономической деятельности с нормами уголовного зак Шесть пороков, разрушающих бхакти
Шесть пороков, разрушающих бхакти Презентация Основные парадигмы политики
Презентация Основные парадигмы политики Табличка на стол (только для CI Дилеров)
Табличка на стол (только для CI Дилеров)