Содержание
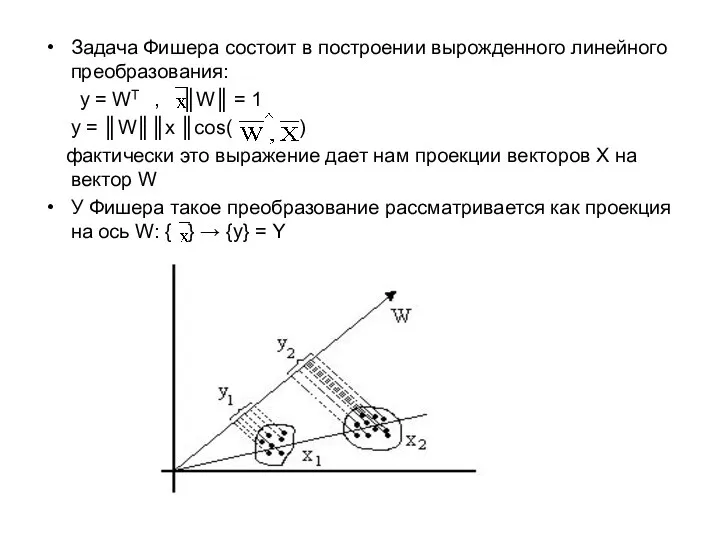
- 2. Задача Фишера состоит в построении вырожденного линейного преобразования: y = WT , ║W║ = 1 y
- 3. Нужно найти такой вектор W, чтобы множества Y1 и Y2 были наиболее разнесены (то есть, удалены
- 4. Далее проблема состоит в оценке функции разброса: = (y - )2 - разброс внутри класса =
- 5. Далее идет дело техники: как это вычислить и как оптимизировать. Мы определяем матрицу разброса внутри класса:
- 6. Таким образом получаем следующий результат: = WT Si W S1 + S2 = SW - суммарная
- 7. Тогда мы получаем искомый критерий в следующем виде: J( ) = Далее стоит задача оптимизации данного
- 8. 3. ранг матрицы SB равен единице, это легко показать, если представить ее в виде ddT: d1d1
- 9. Условная оптимизация по Лагранжу Запишем функцию Лагранжа: F = WT SB W - λ WT SW
- 10. C( ) = λ SW , отсюда окончательно имеем: = SW-1 ( ) . Так как
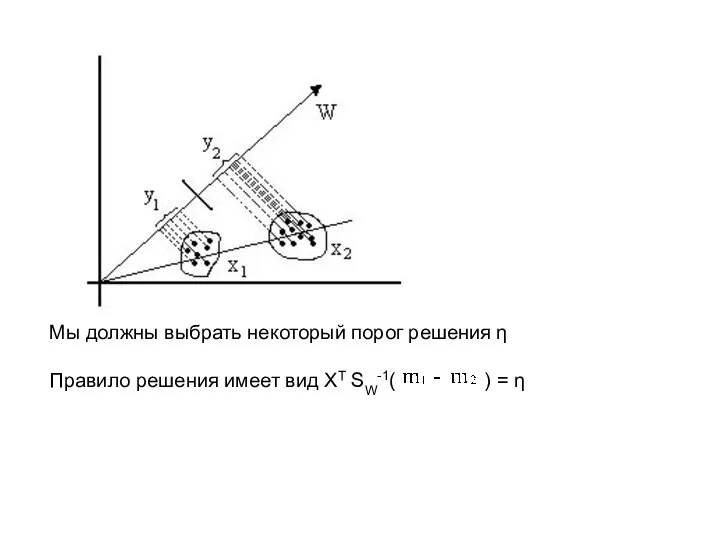
- 11. Мы должны выбрать некоторый порог решения η Правило решения имеет вид XT SW-1( ) = η
- 13. Скачать презентацию








 Трансформаторы. Назначение и принцип работы
Трансформаторы. Назначение и принцип работы Презентация Легальные и нелегальные каналы контрабанды
Презентация Легальные и нелегальные каналы контрабанды Олимпиада. История. Виды спорта
Олимпиада. История. Виды спорта Эффективное резюме
Эффективное резюме АЗБУКИ И БУКВАРИ В СОВРЕМЕННОЙ НАЧАЛЬНОЙ ШКОЛЕ
АЗБУКИ И БУКВАРИ В СОВРЕМЕННОЙ НАЧАЛЬНОЙ ШКОЛЕ  Построение блок-схем к задачам линейной, разветвляющей и циклической структур
Построение блок-схем к задачам линейной, разветвляющей и циклической структур знакомство с gimp
знакомство с gimp  Әкімшілік құқық бойынша тәртіптік-құқықтық мәжбүрлеу
Әкімшілік құқық бойынша тәртіптік-құқықтық мәжбүрлеу Измерения без линейки в формате
Измерения без линейки в формате Émile Benveniste
Émile Benveniste Радіолокація. Історія розвитку радіолокації
Радіолокація. Історія розвитку радіолокації Спортивные сооружения. Лекция 4. Спортивные залы. Тренажерные устройства спортивного зала
Спортивные сооружения. Лекция 4. Спортивные залы. Тренажерные устройства спортивного зала Материалы для подготовки к сочинению-рассуждению на лингвистическую тему
Материалы для подготовки к сочинению-рассуждению на лингвистическую тему Агент плюс
Агент плюс Тренируем руку. Правила написания иероглифов
Тренируем руку. Правила написания иероглифов Организация ветвления на языке Паскаль
Организация ветвления на языке Паскаль SWOT-анализ и его использование в стратегическом анализе Работа ст.гр. ОА-081 Ульянич Т.Ф.
SWOT-анализ и его использование в стратегическом анализе Работа ст.гр. ОА-081 Ульянич Т.Ф.  Система имитационного моделирования GPSS World
Система имитационного моделирования GPSS World Текущая стоимость и скрытые издержки капитала
Текущая стоимость и скрытые издержки капитала Уровни и виды тестирования
Уровни и виды тестирования Системы программного управления промышленными установками
Системы программного управления промышленными установками Способы доступа абонента к сети Интернет
Способы доступа абонента к сети Интернет The Pyongyang Joint Declaration (после)
The Pyongyang Joint Declaration (после) Обяви за работа Подбор Работа Какво да (не) правим. - презентация_
Обяви за работа Подбор Работа Какво да (не) правим. - презентация_ Травматизм. Механическая травма.
Травматизм. Механическая травма.  Презентация на тему "ФУНКЦИОНАЛЬНАЯ СИСТЕМА ВЫДЕЛЕНИЯ" - скачать презентации по Медицине
Презентация на тему "ФУНКЦИОНАЛЬНАЯ СИСТЕМА ВЫДЕЛЕНИЯ" - скачать презентации по Медицине Herbst-Feste in Deutchland. 6 класс
Herbst-Feste in Deutchland. 6 класс Игра по линейному алгоритму
Игра по линейному алгоритму