Содержание
- 2. Оценка качества классификации Рассмотрим случайную величину: являющейся значением решающей функции. Решение принимается сравнением U с порогом
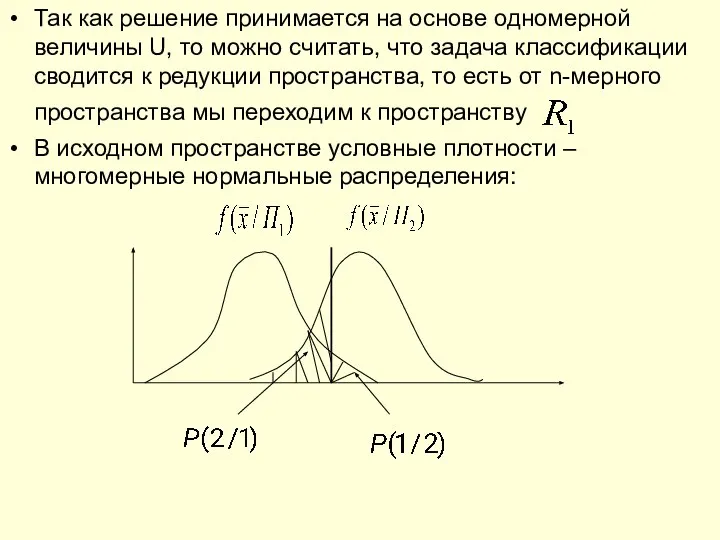
- 3. Так как решение принимается на основе одномерной величины U, то можно считать, что задача классификации сводится
- 4. В редуцированном пространстве переходим к одномерным условным нормальным распределения величины U т. е. каждому многомерному распределению
- 5. Прямое вычисление ошибок в многомерном пространстве приводит к техническим трудностям, поэтому и применяется редукция пространства. Основная
- 6. Условные математические ожидании и дисперсии U по классам где - расстояние Махаланобиса Посчитаем : математические ожидания
- 7. Нахождении дисперсий данной величины В предположении равенства матриц ковариации в исходном пространстве, получаем, что дисперсии U
- 8. U может принадлежать двум нормальным распределениям: U1 ∈ N( (½)α, α); U2 ∈ N(- (½)α, α);
- 9. α - обобщенное расстояние между классами в N-мерном пространстве. α = (M1 - M2)T Σ-1(M1-M2) Если
- 10. α хорошо описывает статистическую природу данных. δ = XT Σ-1(M1 - M2) – (½) (M1 +
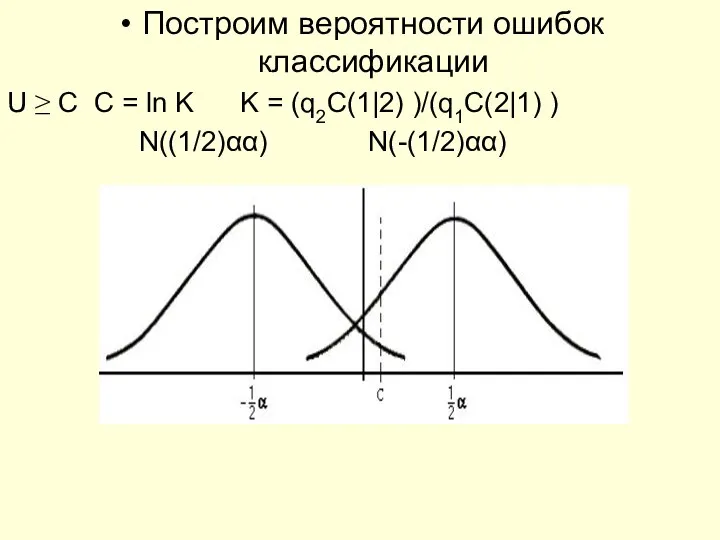
- 11. Построим вероятности ошибок классификации U ≥ C C = ln K K = (q2C(1|2) )/(q1C(2|1) )
- 12. P = q1 P(2|1) + q2 P(1|2) - вероятность полной ошибки Ф(x) – интеграл ошибок Гаусса.
- 13. Полная ошибка Cвойства полной ошибки: C = ln K = ln((q2C(1|2))/(q1C(2|1))) = 0 q1 = q2
- 14. Рассмотрим α Пусть α = (M1 - M2)T Σ-1(M1-M2) = Если σi2 = 1, тогда α
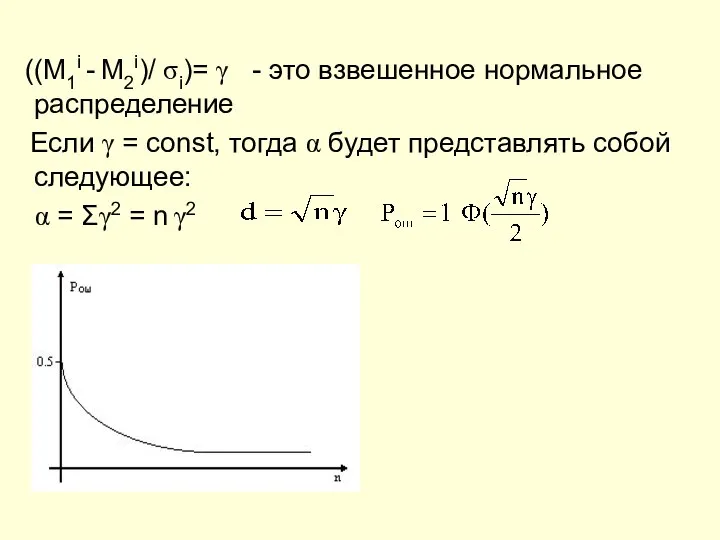
- 15. ((M1i - M2i)/ σi)= γ - это взвешенное нормальное распределение Если γ = const, тогда α
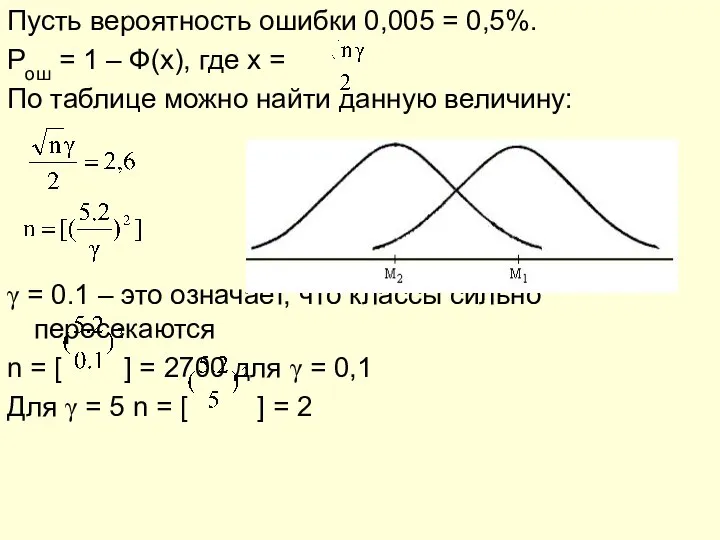
- 16. Пусть вероятность ошибки 0,005 = 0,5%. Pош = 1 – Ф(x), где х = По таблице
- 18. Скачать презентацию











 Презентация на тему "Пища для ума или питание перед экзаменом" - скачать презентации по Педагогике
Презентация на тему "Пища для ума или питание перед экзаменом" - скачать презентации по Педагогике Загадки звучалки - презентация для начальной школы
Загадки звучалки - презентация для начальной школы ПРОБЛЕМЫ СИСТЕМАТИЧЕСКИХ И СЛУЧАЙНЫХ ОШИБОК
ПРОБЛЕМЫ СИСТЕМАТИЧЕСКИХ И СЛУЧАЙНЫХ ОШИБОК Презентация на тему "Воспитание социально-значимой личности" - скачать презентации по Педагогике
Презентация на тему "Воспитание социально-значимой личности" - скачать презентации по Педагогике Янтарная комната История одного из самого загадочного культурного сокровища России
Янтарная комната История одного из самого загадочного культурного сокровища России Здоровый образ жизни
Здоровый образ жизни Формы, валидация данных в JavaScript
Формы, валидация данных в JavaScript Трехуровневая архитектура БД, модель взаимодействия
Трехуровневая архитектура БД, модель взаимодействия Музейные встречи
Музейные встречи Самоконтроль по теме «Реквизиты. Правила оформления документов»
Самоконтроль по теме «Реквизиты. Правила оформления документов» ЦЕЛЬ: Воспитание правовой культуры школьников
ЦЕЛЬ: Воспитание правовой культуры школьников ОБСЛЕДОВАНИЕ ПРИ ДИЗАРТРИИ
ОБСЛЕДОВАНИЕ ПРИ ДИЗАРТРИИ  Прогнозирование модных тенденций на 2020 год по циклам мод
Прогнозирование модных тенденций на 2020 год по циклам мод Энергоэффективные дома
Энергоэффективные дома Баскетбол. Правила игры
Баскетбол. Правила игры Татар халык күлмәкләре
Татар халык күлмәкләре Семлев Т-082
Семлев Т-082  Условный оператор
Условный оператор Противоправное деяние. Преступление
Противоправное деяние. Преступление Устройство цифровой камеры. Прохождение света
Устройство цифровой камеры. Прохождение света Алгоритм Forel. Выделение устойчивых таксонов
Алгоритм Forel. Выделение устойчивых таксонов Язык программирования Паскаль
Язык программирования Паскаль Государственная кадастровая оценка земель сельскохозяйственного назначения. Методическое и технологическое обеспечение оценки
Государственная кадастровая оценка земель сельскохозяйственного назначения. Методическое и технологическое обеспечение оценки Kazakhstan war berühmt mit alten Kultur foods
Kazakhstan war berühmt mit alten Kultur foods Страничка о себе
Страничка о себе Преимущества и недостатки систем охлаждения ПК
Преимущества и недостатки систем охлаждения ПК ТИ АБІТУРІЄНТ ?! Презентація студента. Пацерук О. - презентация
ТИ АБІТУРІЄНТ ?! Презентація студента. Пацерук О. - презентация Методология проектирования БД - Логическое проектирование
Методология проектирования БД - Логическое проектирование