МЕТОД ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА 3.2. ПРОЕЦИРОВАНИЕ ПРЯМОГО УГЛА 3.3. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ

Сентябрь 3, 2022

Главная
Алгебра
МЕТОД ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА 3.2. ПРОЕЦИРОВАНИЕ ПРЯМОГО УГЛА 3.3. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ

Содержание

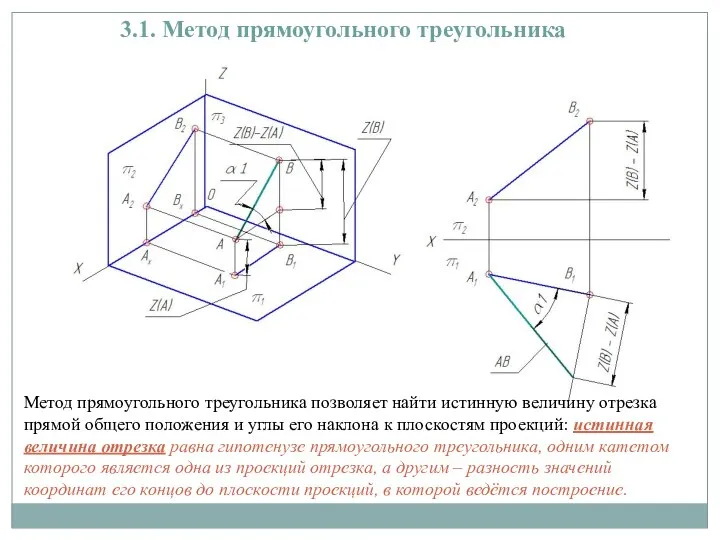
2. 3.1. Метод прямоугольного треугольника Метод прямоугольного треугольника позволяет найти истинную величину отрезка прямой общего положения и
3. Чтобы найти истинную величину отрезка общего положения необходимо: К одной из проекций отрезка (к любой проекции
4. Прямой угол проецируется на плоскость без искажения, если хотя бы одна из сторон этого угла данной
5. 3.3. Взаимное расположение прямых Прямые могут быть: пересекающимися; параллельными; скрещивающимися. 3.3.1. Пересекающиеся прямые – это прямые,
6. 3.3.2. Параллельные прямые – это прямые, пересекающиеся в несобственной точке (в точке, значительно удаленной от наблюдателя).
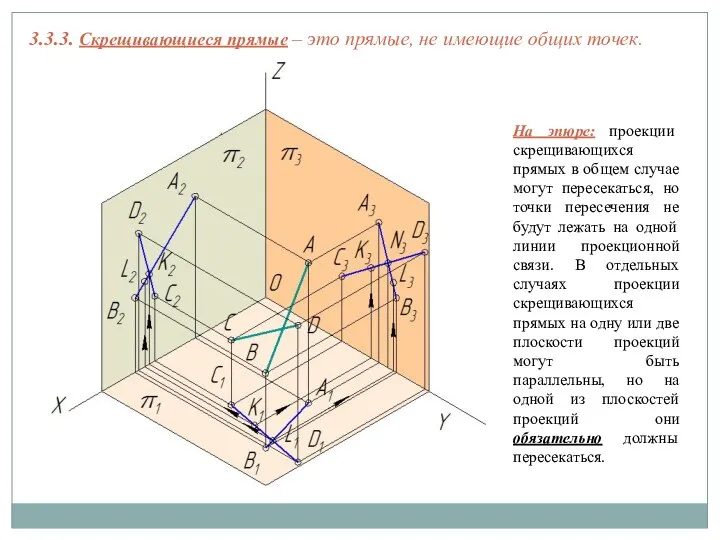
7. 3.3.3. Скрещивающиеся прямые – это прямые, не имеющие общих точек. На эпюре: проекции скрещивающихся прямых в
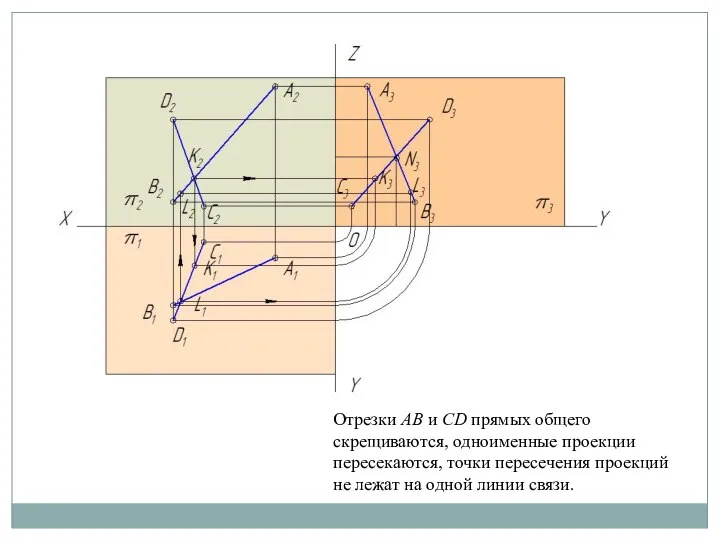
8. Отрезки АВ и CD прямых общего скрещиваются, одноименные проекции пересекаются, точки пересечения проекций не лежат на
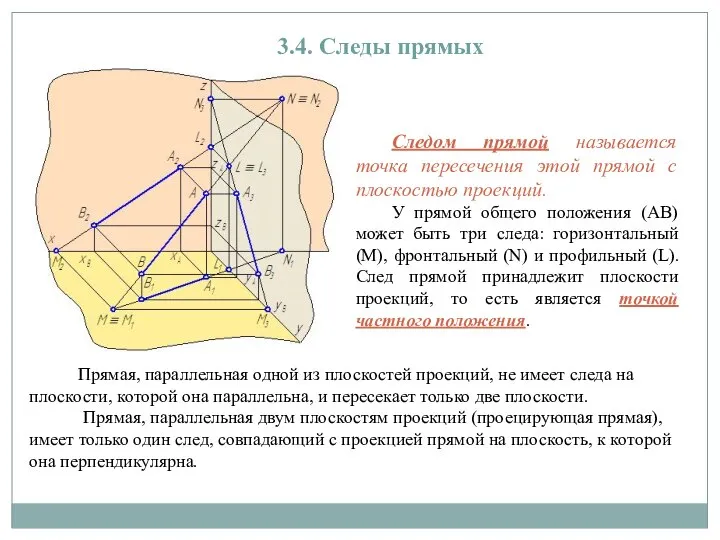
9. 3.4. Следы прямых Следом прямой называется точка пересечения этой прямой с плоскостью проекций. У прямой общего
11. Скачать презентацию

Слайд 2

3.1. Метод прямоугольного треугольника
Метод прямоугольного треугольника позволяет найти истинную величину отрезка

прямой общего положения и углы его наклона к плоскостям проекций: истинная величина отрезка равна гипотенузе прямоугольного треугольника, одним катетом которого является одна из проекций отрезка, а другим – разность значений координат его концов до плоскости проекций, в которой ведётся построение.

Слайд 3

Чтобы найти истинную величину отрезка общего положения необходимо:
К одной из проекций

отрезка (к любой проекции отрезка
(А1 В1) и из любой проекции точек (В1), ограничивающих этот отрезок) восстановить перпендикуляр;
По этому перпендикуляру отложить отрезок, длина которого соответствует разности значений расстояний концов отрезка до плоскости проекций (Z(B) – Z(A)), в которой ведётся построение (π1);
Концы двух катетов соединить, длина полученной гипотенузы (АВ) в прямоугольном треугольнике и будет соответствовать искомому значению;
Угол наклона между гипотенузой и проекцией отрезка (α1) равен углу наклона отрезка к данной плоскости проекций.

Слайд 4

Прямой угол проецируется на плоскость без искажения, если хотя бы одна

из сторон этого угла данной плоскости параллельна, а другая – ей не перпендикулярна: например,
∟АВС = 900 , его сторона АВ ∕∕ π2 , то есть является фронталью ,
поэтому на плоскость π2 этот угол проецируется в истинную величину.

3.2. Проецирование прямого угла

Слайд 5

3.3. Взаимное расположение прямых
Прямые могут быть: пересекающимися; параллельными; скрещивающимися.
3.3.1. Пересекающиеся прямые

– это прямые, имеющие общую точку, то есть точку, в которой они пересекаются.

Слайд 6

3.3.2. Параллельные прямые – это прямые, пересекающиеся в несобственной точке (в

точке, значительно удаленной от наблюдателя).

На эпюре: одноименные проекции параллельных прямых (АВ и CD параллельны) попарно параллельны (А1 В1 ∕∕ C1 D1, А 2 В2 ∕∕ C2 D 2, А3 В3 ∕∕ C3 D3 ).

Слайд 7

3.3.3. Скрещивающиеся прямые – это прямые, не имеющие общих точек.
На эпюре:

проекции скрещивающихся прямых в общем случае могут пересекаться, но точки пересечения не будут лежать на одной линии проекционной связи. В отдельных случаях проекции скрещивающихся прямых на одну или две плоскости проекций могут быть параллельны, но на одной из плоскостей проекций они обязательно должны пересекаться.

Слайд 8

Отрезки АВ и CD прямых общего скрещиваются, одноименные проекции пересекаются, точки

пересечения проекций не лежат на одной линии связи.

Слайд 9

3.4. Следы прямых
Следом прямой называется точка пересечения этой прямой с плоскостью

проекций.
У прямой общего положения (АВ) может быть три следа: горизонтальный (М), фронтальный (N) и профильный (L). След прямой принадлежит плоскости проекций, то есть является точкой частного положения.

Прямая, параллельная одной из плоскостей проекций, не имеет следа на плоскости, которой она параллельна, и пересекает только две плоскости.
Прямая, параллельная двум плоскостям проекций (проецирующая прямая), имеет только один след, совпадающий с проекцией прямой на плоскость, к которой она перпендикулярна.

МЕТОД ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА 3.2. ПРОЕЦИРОВАНИЕ ПРЯМОГО УГЛА 3.3. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ

Содержание

3.1. Метод прямоугольного треугольникаМетод прямоугольного треугольника позволяет найти истинную величину отрезка

Чтобы найти истинную величину отрезка общего положения необходимо:К одной из проекций

Прямой угол проецируется на плоскость без искажения, если хотя бы одна

3.3. Взаимное расположение прямыхПрямые могут быть: пересекающимися; параллельными; скрещивающимися.3.3.1. Пересекающиеся прямые