Содержание
- 2. Балансовые таблицы Для наглядного выражения взаимной связи между отраслями используются таблицы, которые называются таблицами межотраслевого баланса.
- 3. Условия анализа Народное хозяйство разбито на некоторое число и отраслей, которые производят свой однородный продукт, причем
- 4. Условия моделирования Имеется n различных отраслей О1,,..., Оn, каждая из которых производит свой продукт. Отрасль Оi
- 5. Исходные данные модели Xi,- общий объем продукции i отрасли за данный промежуток времени - валовой выпуск
- 6. Балансовая таблица
- 7. Баланс отраслей Балансовый характер этой таблицы выражается в том, что при любом i = 1, ...,
- 8. Формализация балансовой модели Единицы измерения всех указанных величин могут быть или натуральными (кубометры, тонны, штуки, киловатт-часы
- 9. Формализация балансовой модели Величины аij=xij/Xj остаются постоянными в течение ряда лет. Это обусловливается примерным постоянством используемой
- 10. Формализация балансовой модели Согласно гипотезе линейности имеем xij = aij*Xj (i,j= l,...,n). Коэффициенты аij называют коэффициентами
- 11. Формализация балансовой модели В предположении линейности соотношения модели принимают вид: Х1 = а11*x1 + а12*х2 +
- 12. Матричная форма модели X= Ах+у, a11 a12 a1n X1 Y1 А = а21 а22 ...a2n X
- 13. Модель Леонтьева Вектор X называется вектором валового выпуска, вектор Y - вектором конечного потребления, а матрица
- 14. Планирование с помощью балансовой модели Уравнения межотраслевого баланса используют для целей планирования. В этом случае задача
- 15. Нужно решить задачу: сколько следует произвести продукции различных видов, чтобы обеспечить заданный уровень конечного потребления? В
- 16. Ограничения модели При этом нужно иметь в виду следующие особенности системы 1. Все компоненты матрицы А
- 17. Продуктивные модели Леонтьева Определение. Матрица А>0 называется продуктивной, если для любого вектора у>0 существует решение х
- 18. Условия продуктивности Теорема 1 (первый критерий продуктивности). Если А >= 0 и для некоторого положительного вектора
- 19. Условия продуктивности Теорема 2 (второй критерий продуктивности). Матрица A2>=0 продуктивна тогда и только тогда, когда матрица
- 20. Условия продуктивности Теорема 3 (третий критерий продуктивности). Матрица А >= 0 продуктивна тогда и только тогда,
- 21. Правила проверки продуктивности Если сумма элементов любого столбца неотрицательной матрицы А меньше 1 , то А
- 22. Запас продуктивности Пусть А >= 0 - продуктивная матрица. Запасом продуктивности матрицы А назовем такое число
- 23. Модель равновесных цен Рассмотрим теперь балансовую модель, двойственную к модели Леонтьева - равновесных цен. Пусть, А
- 24. Обозначим через p=(p1,p2,рn) - вектор цен, i-я координата которого равна цене единицы продукции i-й отрасли; тогда,
- 25. Модель равновесных цен Часть своего дохода эта отрасль потратит на закупку продукции у других отраслей. Так,
- 26. Модель равновесных цен Тогда для выпуска продукции в объеме x1 первой отрасли необходимо потратить на закупку
- 27. Модель равновесных цен Получим равенство: X1P1 = X1(a11p1 + a21 P2 + .. + an1 Рn)
- 28. Модель равновесных цен Аналогично получим для остальных отраслей P2 =(a12p1 + a22 P2 + .. +
- 29. Модель равновесных цен Модель равновесных цен позволяет, зная величины норм добавленной стоимости, прогнозировать цены на продукцию
- 30. Метод наименьших квадратов Метод наименьших квадратов (часто называемый МНК) обычно упоминается в двух контекстах. Во-первых, использование
- 31. Общий линейный метод наименьших квадратов При аппроксимации методом наименьших квадратов аппроксимируемая функция f задается набором N
- 33. При этом коэффициенты cj выбираются таким образом, чтобы минимизировать сумму квадратов отклонений аппроксимирующей функции от заданных
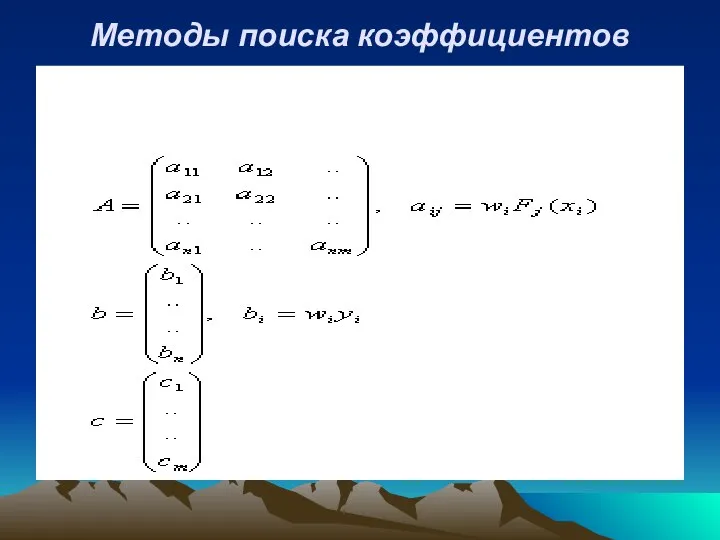
- 34. Методы поиска коэффициентов
- 36. Скачать презентацию






























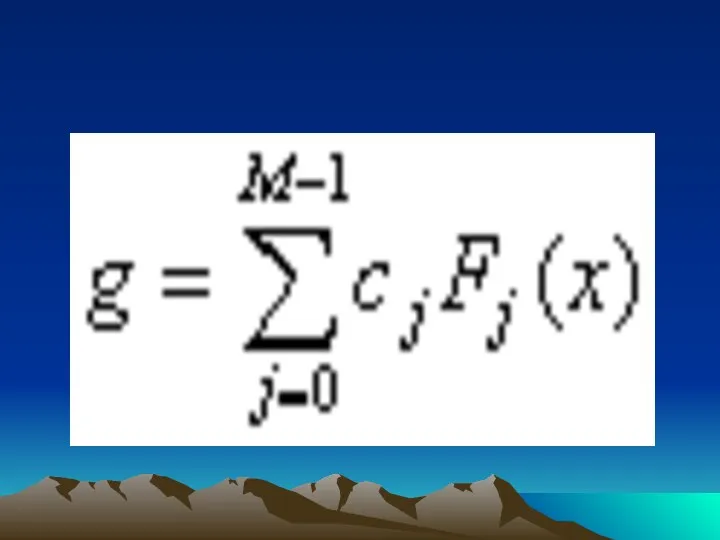

 Неделя семьи. Построение брака и семьи
Неделя семьи. Построение брака и семьи Законы диалектики
Законы диалектики Требования к технологической документации. Справочная, исходная и сопроводительная документация
Требования к технологической документации. Справочная, исходная и сопроводительная документация Решение задач с использованием условного оператора
Решение задач с использованием условного оператора Эрнест Резерфорд
Эрнест Резерфорд Организация технического обслуживания и ремонта автомобиля КамАЗ 6460
Организация технического обслуживания и ремонта автомобиля КамАЗ 6460 Современные подходы к анализу урока русского языка Громова В.И., к.ф.н., доцент кафедры филологического образования СарИПКиПРО
Современные подходы к анализу урока русского языка Громова В.И., к.ф.н., доцент кафедры филологического образования СарИПКиПРО Как празднуют Новый год в разных странах мира
Как празднуют Новый год в разных странах мира Программирование на языке MATLAB. Подпрограммы и функции
Программирование на языке MATLAB. Подпрограммы и функции Православие. Библия
Православие. Библия Тема: « Предмет и задачи этнопедагогики»
Тема: « Предмет и задачи этнопедагогики» Учимся записывать орф задачи
Учимся записывать орф задачи Логические схемы полусумматора и триггера
Логические схемы полусумматора и триггера  Семь чудес света
Семь чудес света  Священный месяц Рамадан
Священный месяц Рамадан Блиц опрос (ДКБ)
Блиц опрос (ДКБ) Информационный сервис “Древо познания” в форме веб-сайта
Информационный сервис “Древо познания” в форме веб-сайта Презентация "Социальный проект" - скачать презентации по Экономике
Презентация "Социальный проект" - скачать презентации по Экономике Презентация Понятия и виды субъектов трудового права
Презентация Понятия и виды субъектов трудового права  Пять самых известных храмов Японии
Пять самых известных храмов Японии Московская Русь
Московская Русь День Конституции России
День Конституции России JavaScript. Основы программирования
JavaScript. Основы программирования Достопримечальности Киева
Достопримечальности Киева Назначение и общий принцип функционирования коммутатора-усилителя. Усилитель мощности: назначение и технические данные. Устройст
Назначение и общий принцип функционирования коммутатора-усилителя. Усилитель мощности: назначение и технические данные. Устройст Operators 413/415. Electromechanical operators for swing gates
Operators 413/415. Electromechanical operators for swing gates Технология Wi-Fi
Технология Wi-Fi Economy of America
Economy of America