Содержание
- 2. 1.Понятие о минимизации ПФ При технической реализации переключательных функций, широко используемых в вычислительной технике, системах автоматического
- 3. 1.Понятие о минимизации ПФ Ограничимся целью нахождения наиболее простого представления переключательной функции в смысле наименьшего числа
- 4. 1.Понятие о минимизации ПФ Методы минимизации разрабатываются применительно к каждой отдельной функциональной полной системе элементных переключательных
- 5. Импликанта и имплицента При минимизации переключательных функций существенную роль играют понятия импликанты, простой импликанты, имплиценты и
- 6. Импликанта Переключательная функция g(х) называется импликантой переключательной функции f(х), если множество рабочих (единичных) наборов функции g(х)
- 7. Имплицента Переключательная функция р(х) является имплицентой переключательной функции f(х), если множество запрещенных (нулевых) наборов функции р(х)
- 8. Склеивание Из СДНФ можно получить другие импликанты путем всевозможных группировок ее членов (конституент) и многократного использования
- 9. Простая импликанта Простой импликантой функции f(х) называется любая элементарная конъюнкция в g(х), являющаяся импликантой функции и
- 10. СкДНФ В булевой алгебре переключательных функций утверждается и доказывается: 1) дизъюнкция любого числа импликант переключательной функции
- 11. Исключение «лишних» простых импликант Иногда из сокращенной ДНФ можно убрать одну или несколько простых импликант, не
- 12. Тупиковые ДНФ Сокращенная ДНФ переключательной функции называется тупиковой, если в ней отсутствуют лишние простые импликанты. Устранение
- 13. ОТДНФ Минимальных ДНФ тоже может быть несколько. Минимальная ДНФ функции, найденная путем построения и перебора всех
- 14. ЧМДНФ Поиск минимальной ДНФ всегда связан с перебором решений. Существуют методы уменьшения перебора, но он всегда
- 15. Минимизация не полностью определенных ПФ При минимизации не полностью определенных переключательных функций особенностью является то, что
- 16. 2.Метод Квайна - Мак -Класки Метод основан на попарном сравнении и склеивании при возможности всех конституент
- 17. 2.Метод Квайна - Мак -Класки Для упорядочения целесообразно разбивать конституенты на группы по числу неинверсированных переменных.
- 18. 2.Метод Квайна - Мак -Класки Мак-Класки формализовал метод Квайна, с целью использования ЭВМ. Формализация заключается в
- 19. 2.Метод Квайна - Мак -Класки Пусть задана функция Сгруппируем эти конституенты единицы по числу единиц:
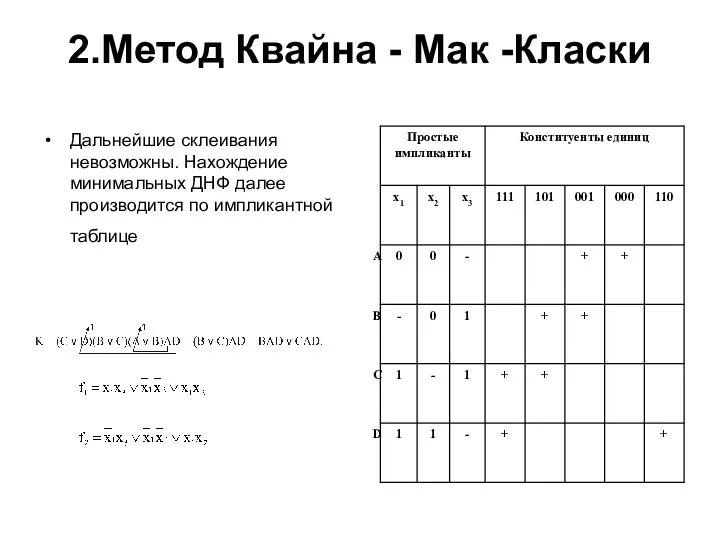
- 20. 2.Метод Квайна - Мак -Класки Дальнейшие склеивания невозможны. Нахождение минимальных ДНФ далее производится по импликантной таблице
- 21. Метод Блейка-Порецкого. Метод Блейка-Порецкого. Метод позволяет получать сокращенную ДНФ булевой функции по ее произвольной ДНФ, а
- 22. 3.Минимизация переключательных функций по картам Карно При решении задач минимизации как полностью определенных, так и не
- 23. Минимизация переключательных функций по картам Карно Метод минимизации по картам Карно позволяет графически получать экономное покрытие
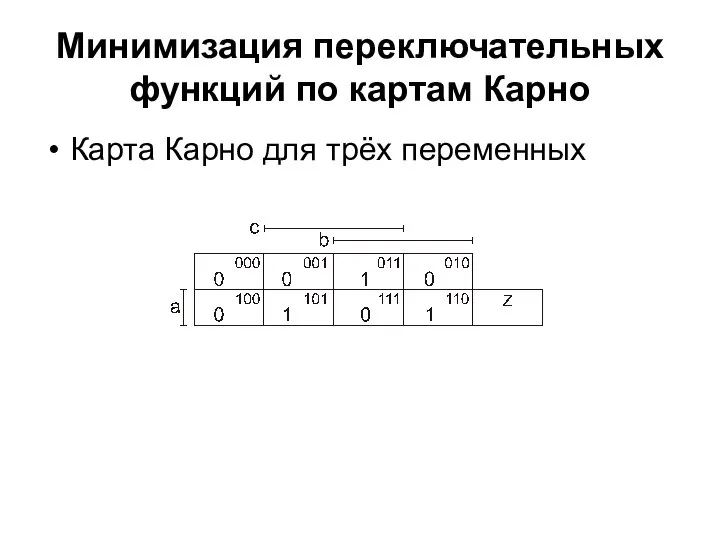
- 24. Минимизация переключательных функций по картам Карно Карта Карно для трёх переменных
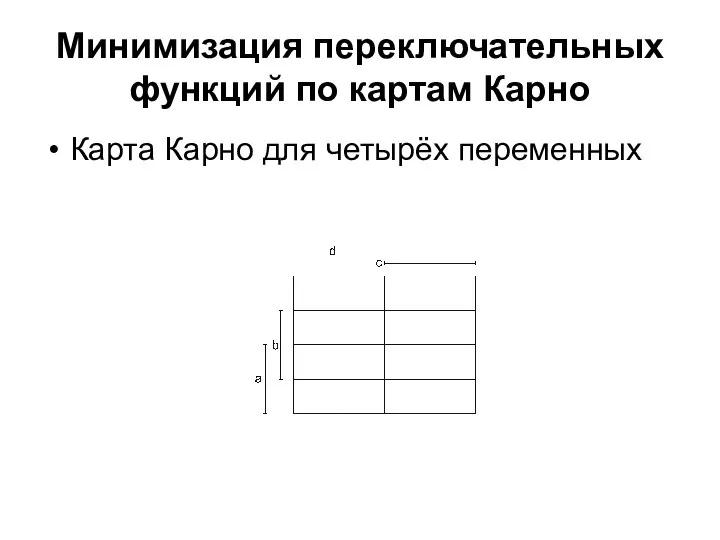
- 25. Минимизация переключательных функций по картам Карно Карта Карно для четырёх переменных
- 26. Минимизация переключательных функций по картам Карно Минимизация переключательной функции по карте Карно в классе ДНФ заключается
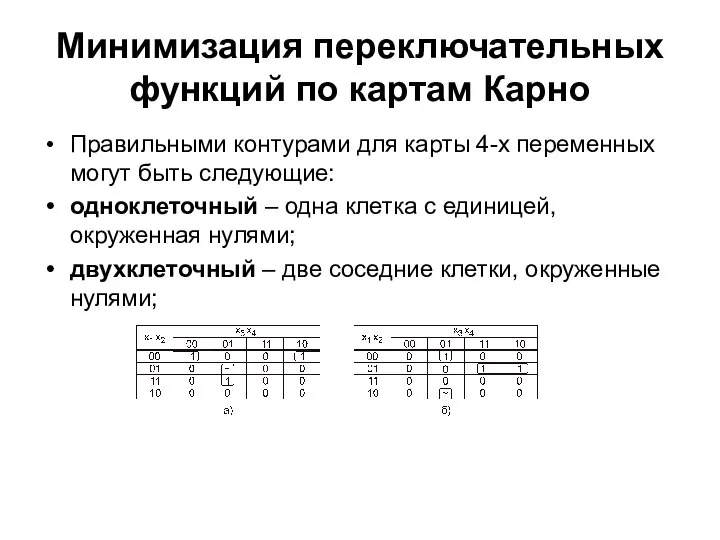
- 27. Минимизация переключательных функций по картам Карно Правильными контурами для карты 4-х переменных могут быть следующие: одноклеточный
- 28. Минимизация переключательных функций по картам Карно четырехклеточный – квадрат из четырех соседних клеток, окруженных нулями;
- 29. Минимизация переключательных функций по картам Карно восьмиклеточный – куб из восьми соседних клеток, окруженных нулями;
- 31. Скачать презентацию
























 Устойчивость откосов и склонов
Устойчивость откосов и склонов Урок, как основная форма работы по физическому воспитанию в начальной школе
Урок, как основная форма работы по физическому воспитанию в начальной школе Central Nervous System
Central Nervous System Достопримечательности Китая
Достопримечательности Китая Орталыќ пост пульт-манипуляторыныњ телебасќару арнасыныњ таратушы ќ±рылѓыларымен байланысы
Орталыќ пост пульт-манипуляторыныњ телебасќару арнасыныњ таратушы ќ±рылѓыларымен байланысы Московский лабиринт
Московский лабиринт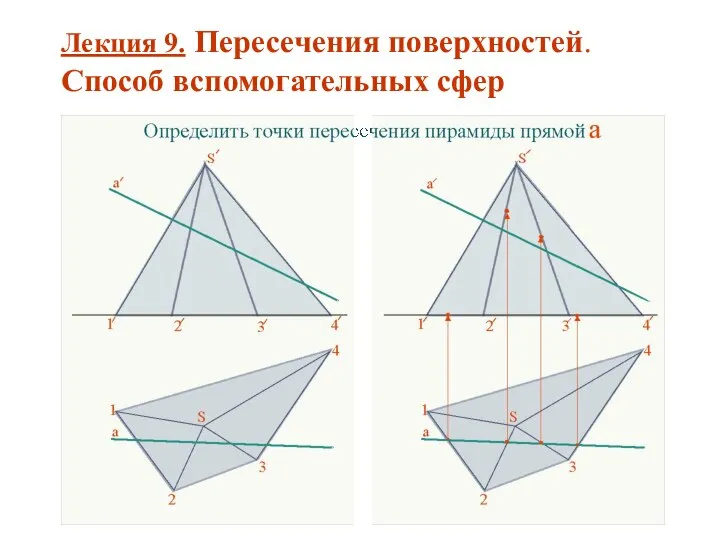 Пересечения поверхностей. Способ вспомогательных сфер. (Лекция 9)
Пересечения поверхностей. Способ вспомогательных сфер. (Лекция 9) Национальная денежно-кредитная политика страны Подготовила: Омельченко Марина, гр.Т-091
Национальная денежно-кредитная политика страны Подготовила: Омельченко Марина, гр.Т-091 Современный этап развития ядерной энергетики.Реакторы на тепловых и быстрых нейтронах
Современный этап развития ядерной энергетики.Реакторы на тепловых и быстрых нейтронах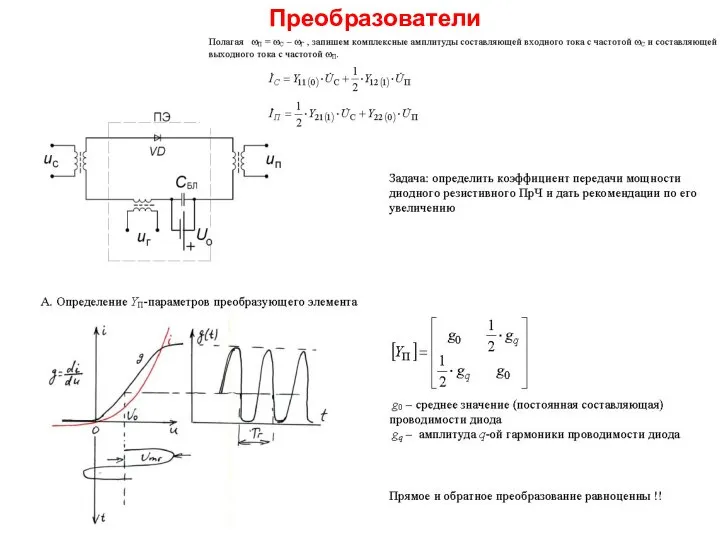 Преобразователи частоты
Преобразователи частоты Достопримечательности Великобритании
Достопримечательности Великобритании Организация, вооружение и боевая техника общевойсковых подразделений Вооружённых Сил Российской Федерации. Общая тактика
Организация, вооружение и боевая техника общевойсковых подразделений Вооружённых Сил Российской Федерации. Общая тактика Preposition maskulinum, femininum, neutrum
Preposition maskulinum, femininum, neutrum Моделирование движения математического маятника в среде с нелинейным сопротивлением на языке программирования Pascal
Моделирование движения математического маятника в среде с нелинейным сопротивлением на языке программирования Pascal Архитектура Древней Руси 11-13 вв.
Архитектура Древней Руси 11-13 вв. Ионные транспортеры и их роль в клетке
Ионные транспортеры и их роль в клетке Дифференциальная диагностика неонатальных желтух Выполнила: Мельчукова Владлена. Гр.51ф 1бр. Преподаватель: Соколова Л. И.
Дифференциальная диагностика неонатальных желтух Выполнила: Мельчукова Владлена. Гр.51ф 1бр. Преподаватель: Соколова Л. И. Опросник описания поведения Томаса
Опросник описания поведения Томаса Коммутационные поля
Коммутационные поля Атраценпроизводные и другие производные антрацена
Атраценпроизводные и другие производные антрацена реанимация 10.09.2018-16.09. 2018
реанимация 10.09.2018-16.09. 2018 Любка Ганна Степанівна - презентация для начальной школы
Любка Ганна Степанівна - презентация для начальной школы Аквааэробика
Аквааэробика ПрезентацияДидактическая игра овощи - презентация для начальной школы
ПрезентацияДидактическая игра овощи - презентация для начальной школы Прості механізми в побуті
Прості механізми в побуті Типы словосочетаний - презентация для начальной школы_
Типы словосочетаний - презентация для начальной школы_ Презентация Налоговая льгота: понятие и классификация
Презентация Налоговая льгота: понятие и классификация Презентация на тему "Инновационные медицинские образовательные программы" - скачать презентации по Медицине
Презентация на тему "Инновационные медицинские образовательные программы" - скачать презентации по Медицине