Содержание
- 2. При изучении дифференциального исчисления рассматривалась задача нахождения производной или дифференциала по заданной функции y=F(x), то есть
- 3. Например, известна скорость перемещения точки v(t), а найти нужно закон ее перемещения: S(t). Эта задача является
- 4. Определение: Дифференцируемая функция F(x) называется первообразной для функции f(x) на интервале (a,b), если F’(x)=f(x) на интервале
- 5. Первообразная для заданной функции f(x) существует только, если эта функция непрерывна на (a,b). Кроме того, первообразных
- 6. Определение: Выражение F(x)+C, где С - произвольная постоянная величина, определяющее множество первообразных для функции f(x) называется
- 7. Знак ∫ - знак неопределенного интеграла; f(x)dx – подынтегральное выражение; f(x) – подынтегральная функция.
- 8. Определение: Операция нахождения первообразной по заданной производной или дифференциалу называется интегрированием. Интегрирование – действие, обратное дифференцированию.
- 9. Придавая постоянной величине С различные значения С1, С2, С3, получим различные функции y1(x)=F(x)+C1, y2(x)=F(x)+C2, y3(x)=F(x)+C3, каждая
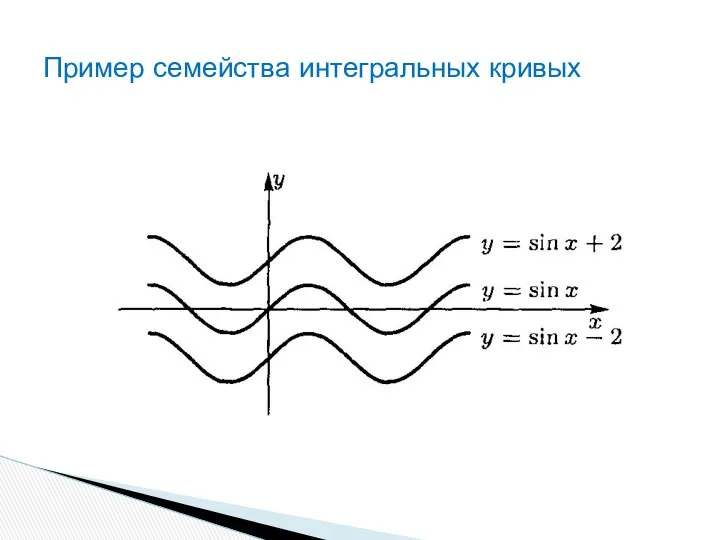
- 10. Следовательно, геометрически неопределенный интеграл представляет собой семейство интегральных кривых.
- 11. Пример семейства интегральных кривых
- 12. Чтобы находить первообразные, необходимо составить и выучить наизусть таблицу неопределенных интегралов от основных элементарных функций. Она
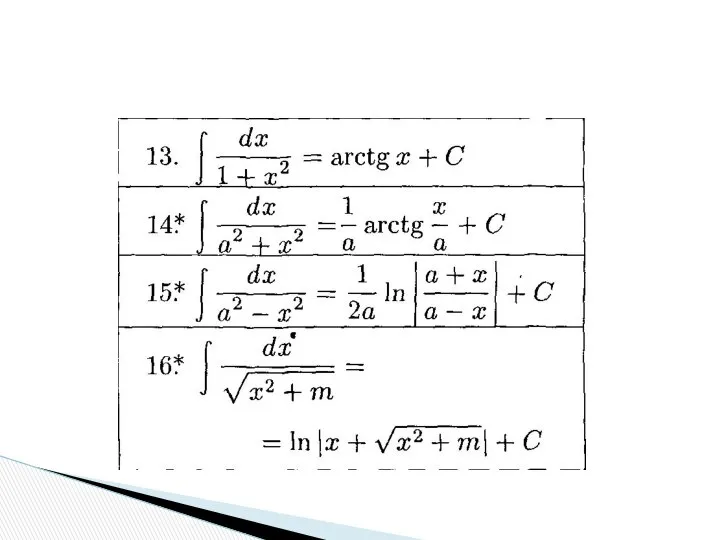
- 13. Таблица основных неопределенных интегралов
- 17. 1) Производная от неопределенного интеграла равна подынтегральной функции. 2. Свойства неопределенных интегралов
- 18. 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:
- 19. 3) Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной:
- 20. 4) Постоянный множитель можно выносить за знак интеграла:
- 21. 5) Интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций:
- 22. Формула интегрирования остается справедливой, если переменная интегрирования является функцией: если
- 23. Этот метод заключается в прямом использовании табличных интегралов и свойств. 3. Непосредственное интегрирование
- 25. Этот метод заключается в разложении подынтегральной функции в линейную комбинацию более простых функций с использованием известных
- 27. Таких методов два: а) метод замены переменной; б) интегрирование по частям. 3. Основные методы интегрирования
- 28. Метод основан на замене переменной в неопределенном интеграле с целью свести его нахождение к нахождению такого
- 29. Пример: Найти неопределенный интеграл: ∫cos2xdx Этот интеграл не является табличным. Произведем замену: y = 2x Тогда
- 30. Дифференциал произведения двух функций определяется формулой: d(u•v) = udv + vdu Интегрируя это равенство, получаем: u•v
- 31. Применение этого метода требует субъективного представления подынтегрального выражения в виде udv, причем интеграл ∫vdu не должен
- 38. Любой результат можно проверить дифференцированием. Например, в последнем случае:
- 41. Скачать презентацию































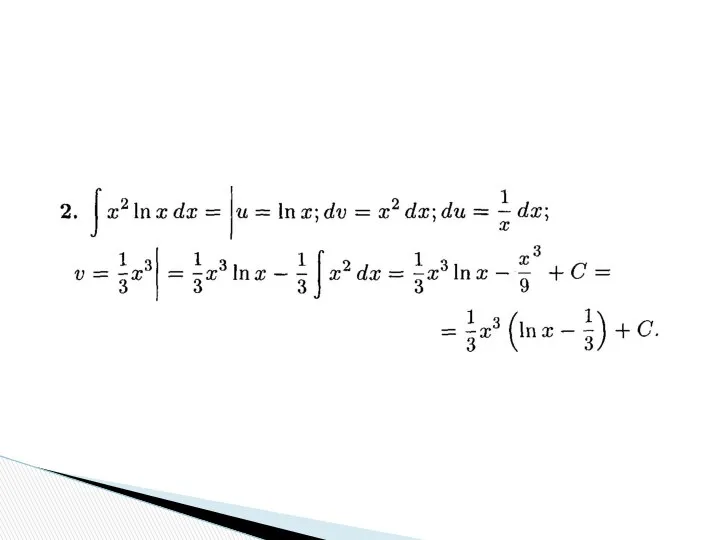
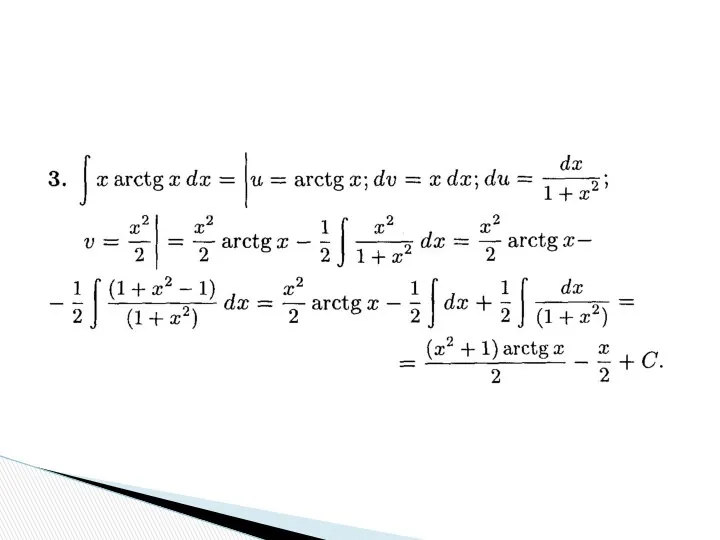



 ДЕНЬГИ И ИХ РОЛЬ В РЫНОЧНОЙ ЭКОНОМИКЕ
ДЕНЬГИ И ИХ РОЛЬ В РЫНОЧНОЙ ЭКОНОМИКЕ  Совершенствование системы разрешения конфликтов в современной организации
Совершенствование системы разрешения конфликтов в современной организации Уравнения Максвелла
Уравнения Максвелла  Позитивизм
Позитивизм  Дефлектор
Дефлектор Указатели Динамические переменные
Указатели Динамические переменные  ВКР:Особенности правового регулирования труда отдельных категорий работников
ВКР:Особенности правового регулирования труда отдельных категорий работников Производственные ресурсы, их формирование и эффективность использования
Производственные ресурсы, их формирование и эффективность использования Apostel Paulus/ Paulus von Tarsus
Apostel Paulus/ Paulus von Tarsus Неоднозначные грамматики. Способы устранения неоднозначности
Неоднозначные грамматики. Способы устранения неоднозначности Education_2_глаголы
Education_2_глаголы Підготовка до різдва на Україні
Підготовка до різдва на Україні Презентация на тему "ДЕПОФОРЕЗ гидроокиси меди-кальция. Эффективность применения при лечении осложненного кариеса" - скачать
Презентация на тему "ДЕПОФОРЕЗ гидроокиси меди-кальция. Эффективность применения при лечении осложненного кариеса" - скачать «ВЕЖЛИВЫЕ» СОВЕТЫ.
«ВЕЖЛИВЫЕ» СОВЕТЫ. Выполнение упражнения вместе с гномиком
Выполнение упражнения вместе с гномиком Қазіргі қытай мәдениетінің ерекшелігі
Қазіргі қытай мәдениетінің ерекшелігі Жиры по органической химии
Жиры по органической химии Посетитель. Компилятор, представляющий программу в виде синтаксического дерева
Посетитель. Компилятор, представляющий программу в виде синтаксического дерева Презентация Валютная система России: структура, характеристики элементов
Презентация Валютная система России: структура, характеристики элементов Презентация на тему "ВМА - КТ в диагностике повреждений области лица" - скачать презентации по Медицине
Презентация на тему "ВМА - КТ в диагностике повреждений области лица" - скачать презентации по Медицине Концепция развития г. Горнозаводска
Концепция развития г. Горнозаводска Числовые характеристики случайных величин
Числовые характеристики случайных величин  Развертки
Развертки Стратегия социальных медиа Vanina Delobelle, PhD www.vaninadelobelle.com Май 2008. - презентация
Стратегия социальных медиа Vanina Delobelle, PhD www.vaninadelobelle.com Май 2008. - презентация Волейбол - олимпийский вид спорта
Волейбол - олимпийский вид спорта Тестовая документация и артефакты тестирования
Тестовая документация и артефакты тестирования Введення. Третя пречиста
Введення. Третя пречиста Основы менеджмента социально-культурной деятельности
Основы менеджмента социально-культурной деятельности