Содержание
- 2. Пусть функция у = f(x) определена на некотором промежутке, и пусть x0 - некоторая точка этого
- 3. Определение. Если существует , то этот предел называется производной от функции у = f(x) по переменной
- 4. Если этот предел конечен, то производная называется конечной, если же этот предел бесконечен, то у'х —
- 5. Пример. Найдем производную у = х2 на основании определения производной. Решение. Δy=(x+Δx)2-x2 = 2x.Δx + (Δx)2.
- 6. Физический смысл - производная функции отражает скорость изменения функции при изменении ее аргумента. Например, если x
- 7. Скорость (быстрота) протекания физических, химических, биологических процессов, например скорость охлаждения тела, скорость химической реакции и т.п.,
- 8. Геометрический смысл: Производная функции у = f(x) геометрически представляет собой угловой коэффициент касательной к графику этой
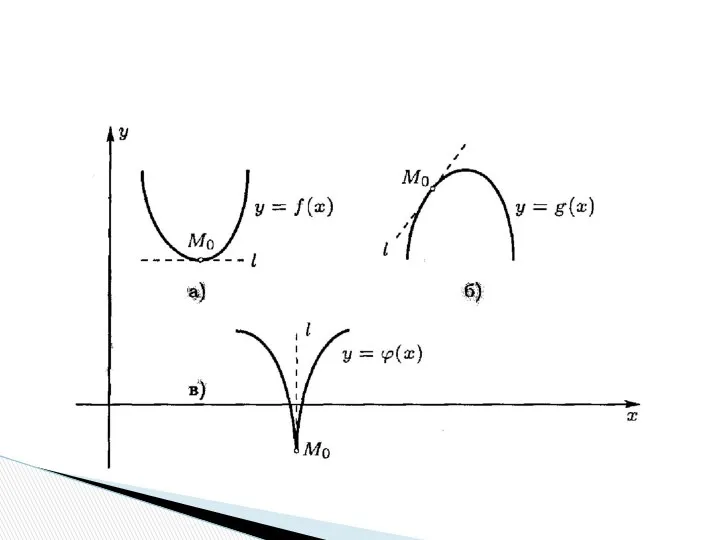
- 10. При этом если существует касательная, то существует и производная, и наоборот. Случаю касательной, не параллельной оси
- 12. Определение: Если приращение функции y = f(x) в точке х можно представить в форме Δy =
- 13. Из последнего равенства следует, что Перейдя к пределу при Δх → 0, получим:
- 14. Итак, если y = f(x) дифференцируема в точке х, то приращение этой функции можно представить в
- 15. Теорема 1 (необходимое условие дифференцируемости): Если функция y = f(x) дифференцируема в точке х, то она
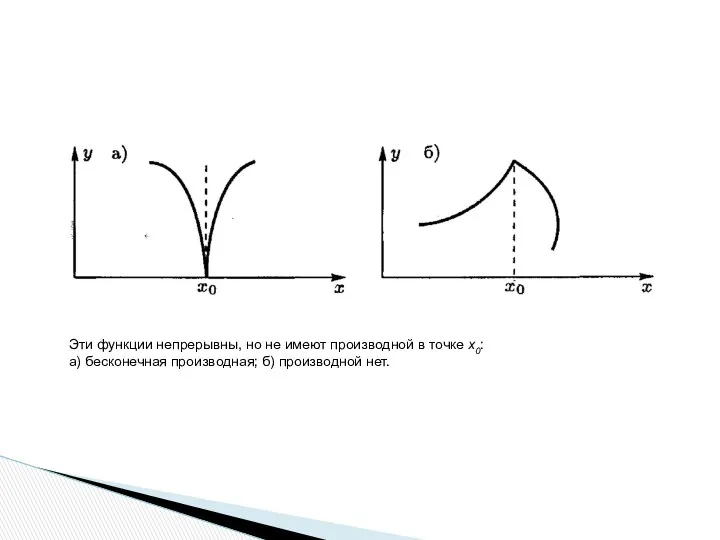
- 16. Эти функции непрерывны, но не имеют производной в точке x0: а) бесконечная производная; б) производной нет.
- 17. 1. Производная от постоянной величины равна нулю, т.е. если y = C, то y’ = 0:
- 18. 2. Производная алгебраической суммы конечного числа функций равна сумме производных слагаемых: (u + v + w
- 19. 3. Производная произведения двух функций определяется формулой: 4. Производная частного от деления двух функций определяется формулой:
- 20. Производные от основных элементарных функций:
- 22. Рассмотрим сложную функцию с одним промежуточным аргументом: у=f(u),u =φ(х), предполагая при этом, что функция у дифференцируема
- 23. На основании определения производной имеем так как предел равен произведению пределов.
- 24. Если учесть, что поскольку всякая дифференцируемая функция непрерывна, то получим, что
- 25. или, в других обозначениях,
- 26. Пример. Найти у', если: у = sin3 5х. Производную этой сложной функции будем находить по формуле
- 27. Предположим, что функция у = f(x) определена, монотонна и дифференцируема в некоторой области, причем производная dy/dx
- 28. Для вывода можно воспользоваться правилом дифференцирования сложной функции с одним промежуточным аргументом. Согласно представлениям о сложной
- 29. На основании правила дифференцирования сложной функции получаем: Поскольку = 1, получаем правило дифференцирования обратной функции:
- 30. Определение. Дифференциалом функции называется произведение производной этой функции на приращение ее аргумента: 3. Дифференциал функции: определение,
- 31. Как видно из определения, дифференциал функции существует лишь для дифференцируемых функций, то есть функций, имеющих производную.
- 32. Рассмотрим следующий пример: Найдем приращение Δy функции y =x2 и дифференциал этой функции: Δy = (x
- 33. Рассмотрим малые приращения аргумента. Например, пусть при x = 1 приращение аргумента равно 0,01. В этом
- 34. Таким образом, дифференциал функции, в общем случае отличаясь от приращения функции, представляет собой главную часть этого
- 35. При достаточно малых приращениях аргумента величина приращения функции приближенно равна дифференциалу этой функции: Δy ≈ dy,
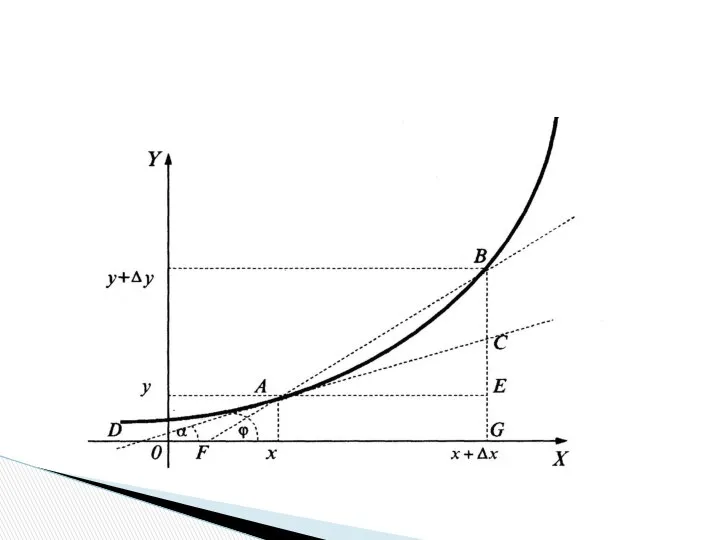
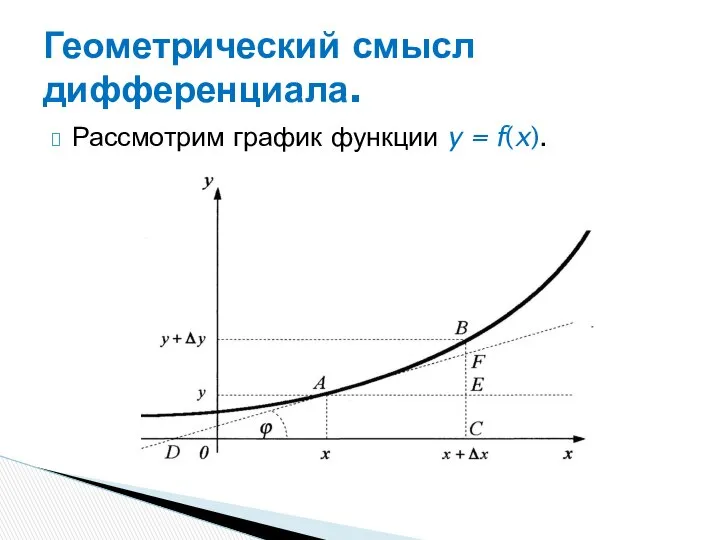
- 36. Рассмотрим график функции y = f(x). Геометрический смысл дифференциала.
- 37. Пусть через точку A (x,y), лежащую на кривой графика функции, проведена касательная DF, образующая угол FDC
- 38. Поскольку углы FAE и FDC равны как соответственные при пересечении параллельных прямых АЕ и DC прямой
- 39. Учитывая, что катет АЕ = Δx, а из геометрического смысла производной следует, что tgφ = y’,
- 40. Рассмотрим функцию, равную своему аргументу: y = x. Тогда дифференциал функции равен дифференциалу аргумента: dy =y’•Δx
- 41. Формулу дифференциала функции можно записать в виде: dy = y’dy, а формулу производной – в виде:
- 43. Скачать презентацию




































 Марли и я. Собака в искусстве
Марли и я. Собака в искусстве Официально деловой стиль русского языка
Официально деловой стиль русского языка Политическая система
Политическая система  Куртуазна література
Куртуазна література Предприятие EcoCorp
Предприятие EcoCorp Проектное обучение ИСТиС
Проектное обучение ИСТиС Мақтаншақ бұлақ
Мақтаншақ бұлақ Семейная Медицина Умид Шарапов
Семейная Медицина Умид Шарапов  Презентация КОРПОРАТИВНЫЕ ЗНАНИЯ В ОРГАНИЗАЦИИ
Презентация КОРПОРАТИВНЫЕ ЗНАНИЯ В ОРГАНИЗАЦИИ Зона комфорта
Зона комфорта  Языкознание как комплексная гуманитарная дисциплина. Языкознание, или лингвистика
Языкознание как комплексная гуманитарная дисциплина. Языкознание, или лингвистика Архитектура Индии
Архитектура Индии Основные характеристики команды проекта
Основные характеристики команды проекта Художественная гимнастика, как искусство
Художественная гимнастика, как искусство Николай Степанович Таганцев (1843 – 1923)
Николай Степанович Таганцев (1843 – 1923) Что поможет мне учиться?
Что поможет мне учиться? Презентация Территориальные рамки Российского централизованного государства к середине XVI века
Презентация Территориальные рамки Российского централизованного государства к середине XVI века  УЧЕТ ТРУДА И ЕГО ОПЛАТЫ Режим рабочего времени организации - это распределение работы в течение конкретного календарного пер
УЧЕТ ТРУДА И ЕГО ОПЛАТЫ Режим рабочего времени организации - это распределение работы в течение конкретного календарного пер Профилактика профессиональной деформации педагогов Опыт работы психологической службы МОУ гимназия №2 г. Раменское Педагог- пс
Профилактика профессиональной деформации педагогов Опыт работы психологической службы МОУ гимназия №2 г. Раменское Педагог- пс Ожирение и метаболический синдром
Ожирение и метаболический синдром Федотов Павел Андреевич 1815, Москва - 1852, Петербург
Федотов Павел Андреевич 1815, Москва - 1852, Петербург Особенности распространения возбуждения в ЦНС
Особенности распространения возбуждения в ЦНС  Компьютерные презентации
Компьютерные презентации  Мосты дружбы. Территория ценностей
Мосты дружбы. Территория ценностей Способы оценки и расчёт результатов биохимического исследования. Средний показатель, референсные и критические значения.
Способы оценки и расчёт результатов биохимического исследования. Средний показатель, референсные и критические значения. Презентация Залог как способ обеспечения исполнения обязательств
Презентация Залог как способ обеспечения исполнения обязательств Занятие физической культурой в послеродовом периоде
Занятие физической культурой в послеродовом периоде Формы, отчеты как продукт анализа БД .
Формы, отчеты как продукт анализа БД .