Содержание
- 2. Тема презентации: Непрерывные коды
- 3. Работу выполнил: Сизых С. Д. Студент группы П-31 Факультета ИВТ, 3-й курса
- 4. Оглавление Классификация кодов Помехоустойчивые коды Блочные коды Понятие о непрерывных кодах Цепной код Сверточные коды
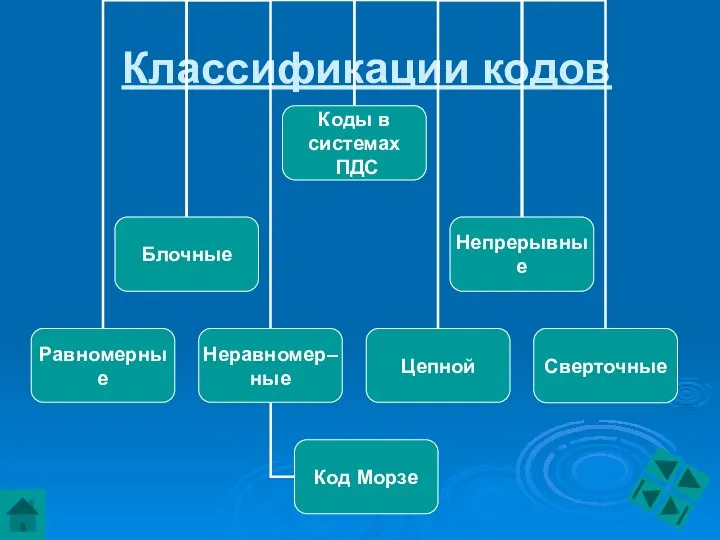
- 5. Классификации кодов
- 6. Классификация кодов
- 7. Помехоустойчивые коды Помехоустойчивые коды делятся на: Блочные Непрерывные К блочным относятся коды, в которых каждому сообщению
- 8. Блочные коды В связи с этим блочные коды делятся на: равномерные, неравномерные. Широкое практическое применение нашли
- 9. Понятие о непрерывных кодах Непрерывные коды, к которым относятся рекуррентные (сверточные), цепной, представляют собой непрерывные последовательностит
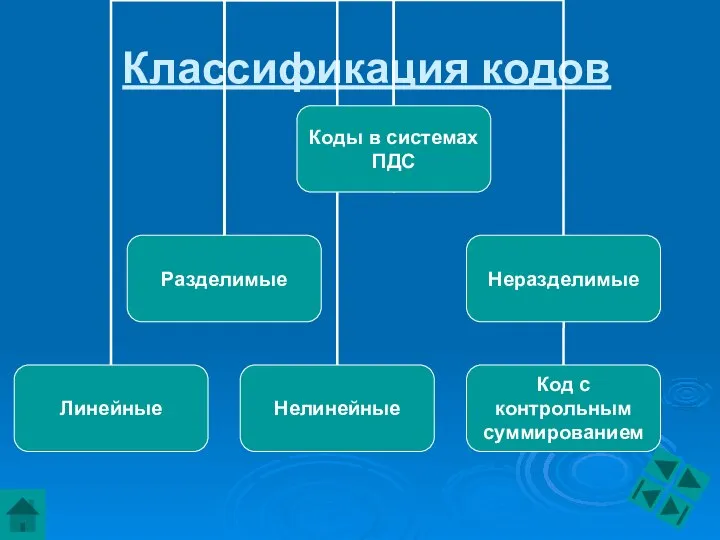
- 10. Блочные коды Разновидностями как блочных, так и непрерывных кодов являются: разделимые (с возможностью выделения информационных и
- 11. Понятие о непрерывных кодах В непрерывных кодах избыточные разряды помещаются в определенном порядке между информационными разрядами.
- 12. Понятие о непрерывных кодах Эти коды применяются для обнаружения и исправления пачек ошибок. Для сверточных кодов
- 13. Цепной код В данном коде после каждого информационного элемента следует проверочный элемент. Проверочные элементы формируются путем
- 14. Цепной код Из информационных элементов (а0, аl), (а1, аl+1), … формируются следующие проверочные элементы по правилу
- 15. Цепной код на приеме выделяются отдельно информационные элементы и отдельно проверочные элементы; из принятой последовательности информационных
- 16. Цепной код При отсутствии ошибок принятые и вычисленные проверочные разряды, очевидно, совпадают. Наличие ошибок приведет к
- 17. Цепной код Рассмотренный цепной код за счет большой избыточности сравнительно просто позволяет обнаруживать или исправлять пачки
- 18. Сверточные коды Рассмотренный цепной код является простейшим случаем сверточных кодов. В основу сверточного кодирования положен принцип
- 19. Сверточные коды Если передача информации происходит по одному каналу, но к выходу кодирующего устройства подключается специальная
- 20. Сверточные коды Выходные проверочные последовательности можно представить в виде n—k полиномов: B(1)(x)=b0(1)+ b1(1)*x+… B(2)(x)=b0(2)+ b1(2)*x+… B(n-k)(x)=b0(n-k)+
- 21. Сверточные коды Полиномы G(j)(x),…, Z(j)(x), называются образующими (по терминологии циклических кодов). Если r — наибольшая степень
- 22. Сверточные коды Для пояснения принципа кодирования рассмотрим случай, когда скорость кода равна k/n=1/2. Тогда число образующих
- 23. Сверточные коды Таким образом, кодирование заключается в вычислении произведения В(х). С учетом того, что операция умножения
- 24. Сверточные коды Если на вход кодирующего устройства информационные символы поступают поочередно, то проверочные разряды bi в
- 25. Сверточные коды Из (7.22) видно, что формирование проверочных разрядов происходит суммированием по модулю 2 каждого информационного
- 27. Скачать презентацию






















 Тема урока АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Тема урока АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ Питание и пища Выполнили: Петрова, Другова Проверила: Трифонова О.Ю
Питание и пища Выполнили: Петрова, Другова Проверила: Трифонова О.Ю Автоматические поточные линии
Автоматические поточные линии ОПЕРАЦИИ ЦЕНТРАЛЬНОГО БАНКА НА ОТКРЫТОМ РЫНКЕ Комаров П. Паркина М. МЭ081
ОПЕРАЦИИ ЦЕНТРАЛЬНОГО БАНКА НА ОТКРЫТОМ РЫНКЕ Комаров П. Паркина М. МЭ081 Разработка модели подсистемы управления освещением
Разработка модели подсистемы управления освещением Сортировка-Пузырёк Выборочная QuickSort
Сортировка-Пузырёк Выборочная QuickSort Презентация "Задачи и организация учета" - скачать презентации по Экономике
Презентация "Задачи и организация учета" - скачать презентации по Экономике Кроссворд по «Истории таможенного дела и таможенной политике» Выполнила студентка 1-ого курса
Кроссворд по «Истории таможенного дела и таможенной политике» Выполнила студентка 1-ого курса  Культура России XVII века
Культура России XVII века Детская сына
Детская сына Все подвиги Геракл совершил на службе А) у Зевса Б) у Эврисфея В) у Алкмены
Все подвиги Геракл совершил на службе А) у Зевса Б) у Эврисфея В) у Алкмены Государственный контроль и надзор в дизайнерской деятельности
Государственный контроль и надзор в дизайнерской деятельности Вода и здоровье.Методы улучшения качества воды.( 2 курс)
Вода и здоровье.Методы улучшения качества воды.( 2 курс)  Ведение буровзрывных работ на горизонте Южной залежи
Ведение буровзрывных работ на горизонте Южной залежи Модуль «ОСНОВЫ СВЕТСКОЙ ЭТИКИ» УРОК 45. РОД И СЕМЬЯ – ИСТОК НРАВСТВЕННЫХ ОТНОШЕНИЙ В ИСТОРИИ ЧЕЛОВЕЧЕСТВА
Модуль «ОСНОВЫ СВЕТСКОЙ ЭТИКИ» УРОК 45. РОД И СЕМЬЯ – ИСТОК НРАВСТВЕННЫХ ОТНОШЕНИЙ В ИСТОРИИ ЧЕЛОВЕЧЕСТВА Серебряный век русской культуры
Серебряный век русской культуры Идентификация контролируемых товаров и технологий Статья 24. Идентификация контролируемых товаров и технологий  
Идентификация контролируемых товаров и технологий Статья 24. Идентификация контролируемых товаров и технологий   Мультиэлектродные массивы (лекция 4)
Мультиэлектродные массивы (лекция 4) Топологическое проектирование ПП
Топологическое проектирование ПП «ДИФФЕРЕНЦИАЛЬНАЯ ДИАГНОСТИКА АНГИН»
«ДИФФЕРЕНЦИАЛЬНАЯ ДИАГНОСТИКА АНГИН» Транспортная безопасность США
Транспортная безопасность США Преимущества и трудности управления персоналом в холдинговых компаниях «Дао не делает ничего, однако ничего не остается не сдела
Преимущества и трудности управления персоналом в холдинговых компаниях «Дао не делает ничего, однако ничего не остается не сдела Презентация Договор ренты
Презентация Договор ренты Интернет-магазин экологически чистых товаров EcoFutureShop
Интернет-магазин экологически чистых товаров EcoFutureShop Р/р ИЗЛОЖЕНИЕ
Р/р ИЗЛОЖЕНИЕ Культура и религия
Культура и религия ГЕРБЫ И ЭМБЛЕМЫ Изобразительное искусство 5 класс
ГЕРБЫ И ЭМБЛЕМЫ Изобразительное искусство 5 класс Обучение технике ударов по мячу в футболе. _
Обучение технике ударов по мячу в футболе. _