Содержание
- 2. Ориентация осей современного максимального горизонтального сжатия SH,max в Западной Европе и континентальной Австралии из мировой базы
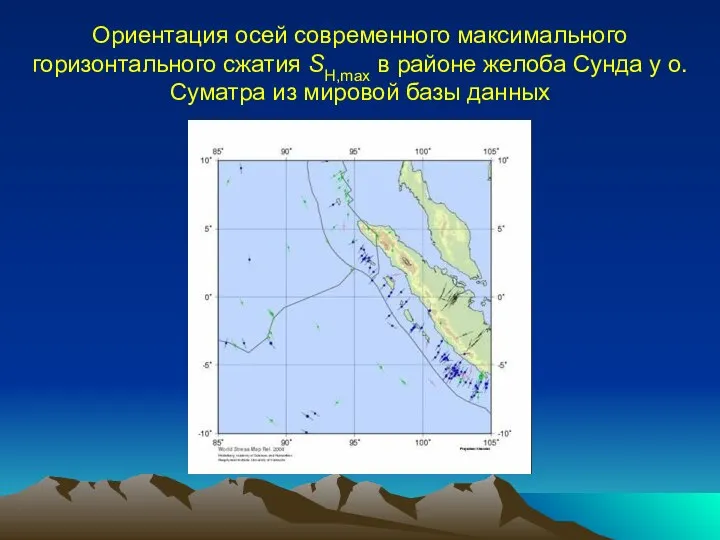
- 3. Ориентация осей современного максимального горизонтального сжатия SH,max в районе желоба Сунда у о. Суматра из мировой
- 4. Ориентация осей современного максимального горизонтального сжатия SH,max в районе конвергенции Аравийской и Евразийской плит из мировой
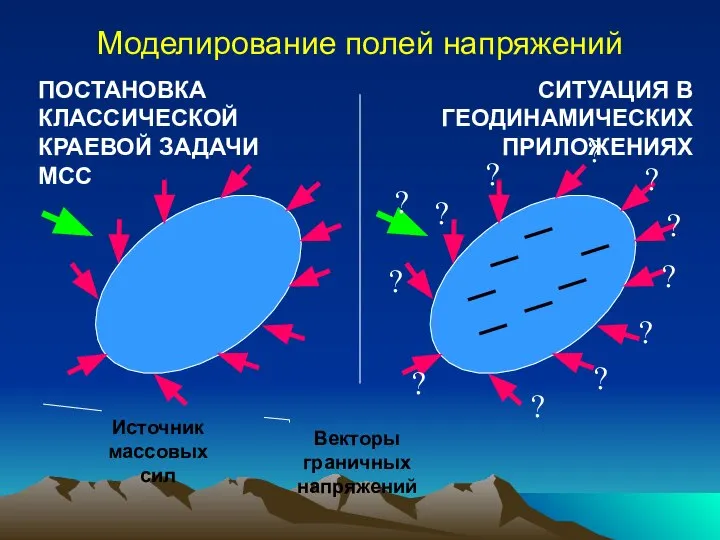
- 5. Моделирование полей напряжений Векторы граничных напряжений ПОСТАНОВКА КЛАССИЧЕСКОЙ КРАЕВОЙ ЗАДАЧИ МСС Источник массовых сил ? СИТУАЦИЯ
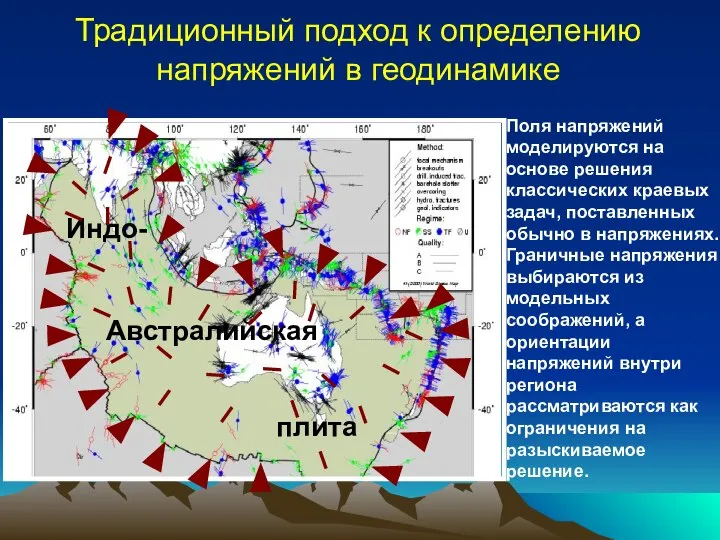
- 6. Поля напряжений моделируются на основе решения классических краевых задач, поставленных обычно в напряжениях. Граничные напряжения выбираются
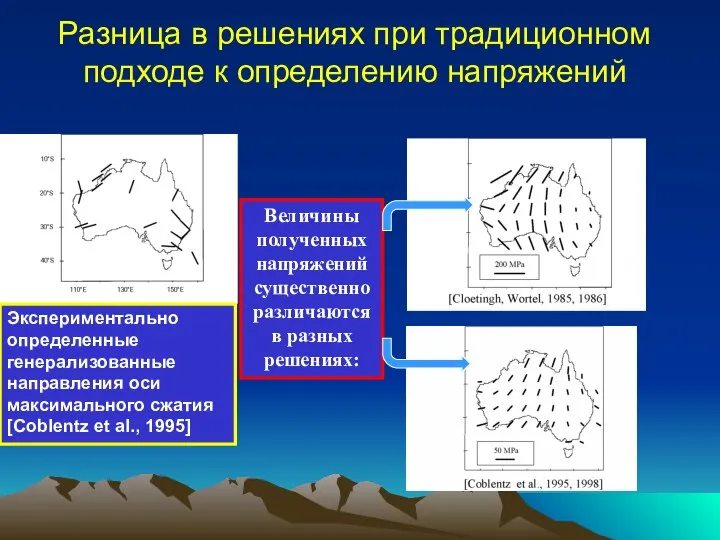
- 7. Величины полученных напряжений существенно различаются в разных решениях: Экспериментально определенные генерализованные направления оси максимального сжатия [Coblentz
- 8. Прямой подход к определению полей напряжений ОСНОВНАЯ ЦЕЛЬ: объединить достоинства измерений напряжений in-situ (реальность характеристик получаемого
- 9. Представление плоского тензора напряжений SH,max SH,min ϕ SH,max и SH,min – взаимно ортогональные главные значения тензора
- 10. Траектории главных напряжений Траектории главных напряжений (ТГН) – кривые, касательные к которым в каждой точке ориентированы
- 11. 2D уравнения равновесия T=T1m1⊗m1+ T2m2⊗m2 В декартовой с.к. x1, x2 с ортами e1, e2 В ортогональной
- 12. 2D уравнения равновесия ϕ − угол наклона T1 к оси x; sj − длина дуги вдоль
- 13. 2D уравнения равновесия Тензор T(x(s)) задан на линии x=x(s) и в окрестности линии известно поле ТГН.
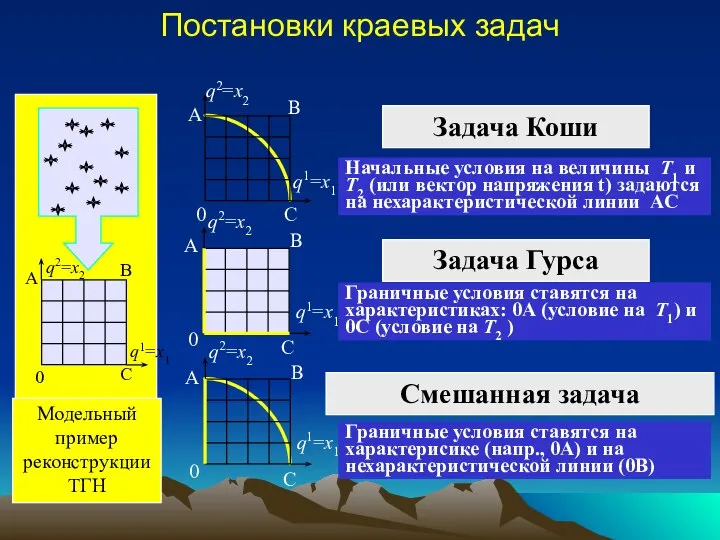
- 14. Модельный пример реконструкции ТГН Постановки краевых задач
- 15. Аналитические решения для простейших ТГН ТГН, совпадающие с линиями декартовой с.к. ТГН, совпадающие с линиями полярной
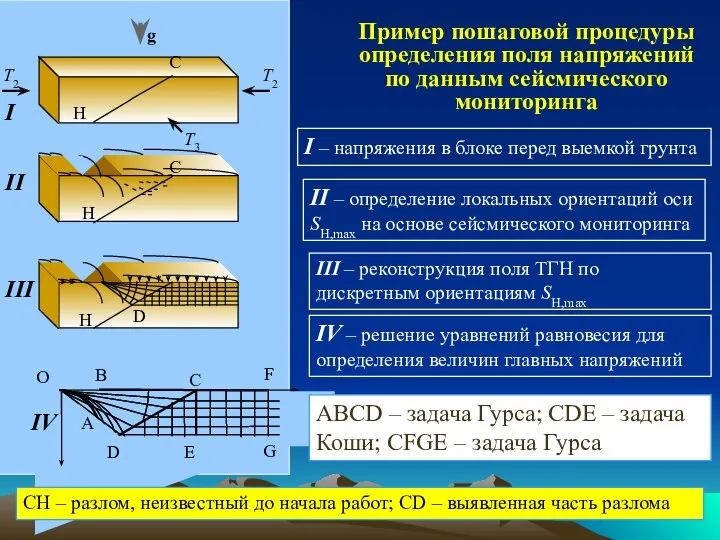
- 16. Пример пошаговой процедуры определения поля напряжений по данным сейсмического мониторинга I – напряжения в блоке перед
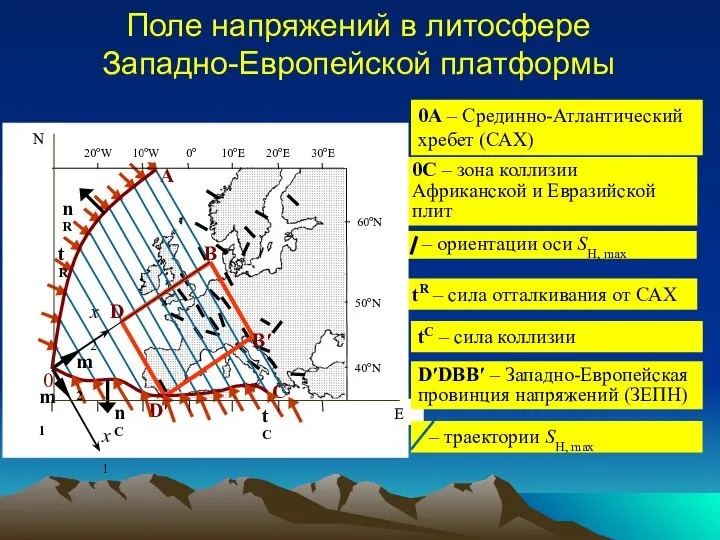
- 17. 0A – Срединно-Атлантический хребет (САХ) 0C – зона коллизии Африканской и Евразийской плит tR – сила
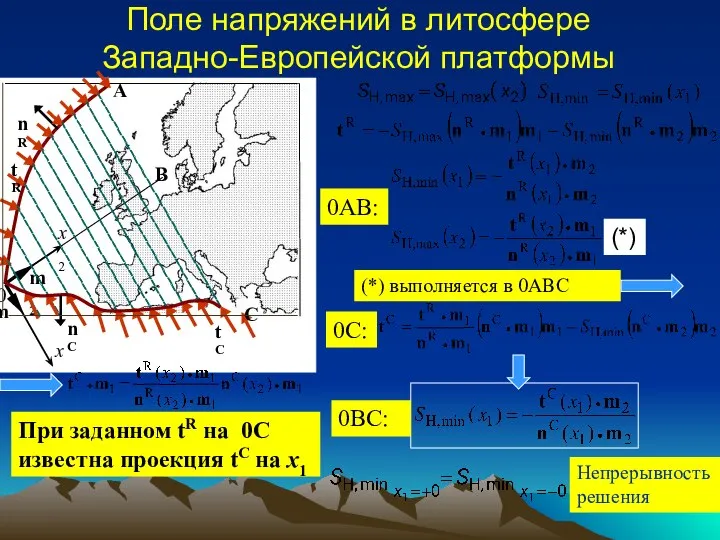
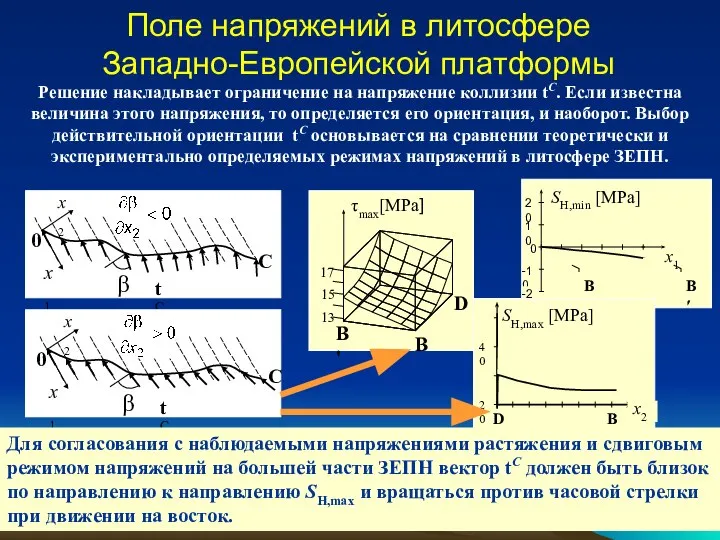
- 18. Поле напряжений в литосфере Западно-Европейской платформы
- 19. Решение накладывает ограничение на напряжение коллизии tC. Если известна величина этого напряжения, то определяется его ориентация,
- 20. Некоторые сведения из ТФКП Δf1=0, Δf2=0 Определить голоморфную функцию f в круге по заданной на границе
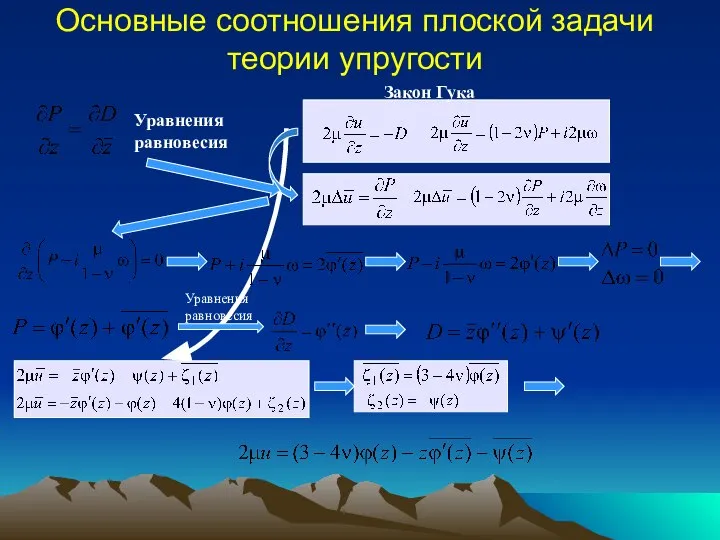
- 21. Основные соотношения плоской задачи теории упругости P – вещественная функция среднего напряжения, D – комплекснозначная функция
- 22. Основные соотношения плоской задачи теории упругости Уравнения равновесия Закон Гука
- 23. Основные соотношения плоской задачи теории упругости Формулы Колосова-Мусхелишвили Φ, Ψ - голоморфные функции, D – биголоморфная
- 24. Общий вид вещественной биголоморфной функции (Im c0 =Im c2 =0) Основные соотношения плоской задачи теории упругости
- 25. Типы задач для упругой литосферы Определение поля напряжений по: Общие свойства решений: 1) решение для поля
- 26. Особые точки первого рода поля траекторий главных напряжений z=0 – особая точка первого порядка T1=T2 при
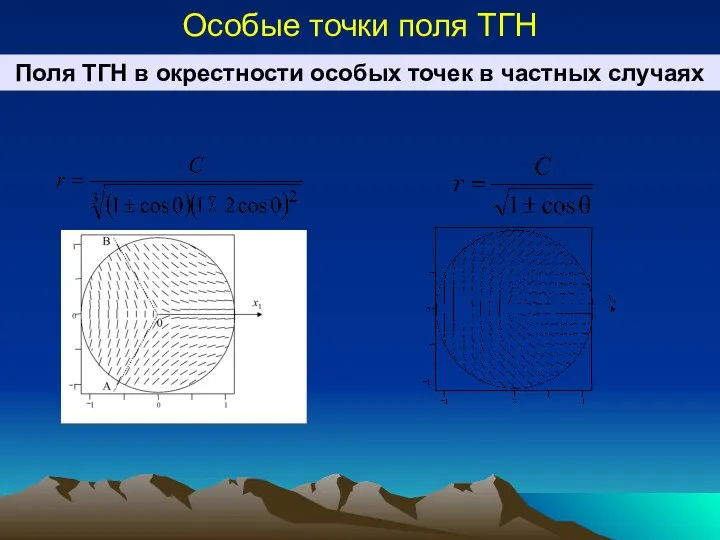
- 27. Особые точки поля ТГН Поля ТГН в окрестности особых точек в частных случаях
- 28. Определение напряжений при заданных ТГН в упругости Не каждое поле траекторий допустимо в упругой среде, т.к.
- 29. Определение напряжений при заданных ТГН в упругости Определить би-голоморфную функцию D по заданному полю ее аргумента
- 30. Частное решение Определение напряжений при заданных ТГН в упругости
- 31. Частное решение (продолжение) Решая задачу для двух кругов r* и r** Определение напряжений при заданных ТГН
- 32. Определение напряжений при заданных ТГН в упругости Общее решение
- 33. Определение напряжений при заданных ТГН в упругости Общее решение на γ является граничным значением голоморфной функции
- 34. Определение напряжений при заданных ТГН в упругости Декартовые ТГН Полярные ТГН
- 35. Определение напряжений при заданных ТГН в упругости Параболические ТГН η=const → →
- 37. Скачать презентацию























 Презентация Память
Презентация Память Производственно-коммерческая компания ООО «Техмашкомплект» г. Ульяновск
Производственно-коммерческая компания ООО «Техмашкомплект» г. Ульяновск Язык ASSEMBLER. Команды пересылки данных
Язык ASSEMBLER. Команды пересылки данных EasyPact TVS – выбор в пользу простоты и гибкости
EasyPact TVS – выбор в пользу простоты и гибкости Презентация Запреты и ограничения во внешней торговле стран членов Таможенного союза
Презентация Запреты и ограничения во внешней торговле стран членов Таможенного союза Решаем примеры и задачи в пределах 20 Выполнила: учитель начальных классов МКВ(с)ОУ г.Астрахани «О(с)ОШ №5» Милькина Юлия Алексеевн
Решаем примеры и задачи в пределах 20 Выполнила: учитель начальных классов МКВ(с)ОУ г.Астрахани «О(с)ОШ №5» Милькина Юлия Алексеевн Презентация "Инвестиционный фонд Российской Федерации как инструмент экономической политики и новые возможности для регионов&
Презентация "Инвестиционный фонд Российской Федерации как инструмент экономической политики и новые возможности для регионов& Степ аэробика. Фитнес-студия "Body Balance"
Степ аэробика. Фитнес-студия "Body Balance" Базовый комплект комплекса разведки, управления и связи БК КРУС-М. Изделие 83т415
Базовый комплект комплекса разведки, управления и связи БК КРУС-М. Изделие 83т415 Организация, вооружение мотострелкового (танкового) батальона
Организация, вооружение мотострелкового (танкового) батальона Спортивные сооружения. Лекция 4. Спортивные залы. Тренажерные устройства спортивного зала
Спортивные сооружения. Лекция 4. Спортивные залы. Тренажерные устройства спортивного зала История развития ислама и исламского права
История развития ислама и исламского права Презентация по алгебре Линейные уравнения с одной переменной 7 класс
Презентация по алгебре Линейные уравнения с одной переменной 7 класс Национальная технологическая инициатива РФ
Национальная технологическая инициатива РФ Правовое регулирование недропользования, правовой режим недр
Правовое регулирование недропользования, правовой режим недр Техногенные опасности
Техногенные опасности  Массивы
Массивы Основные понятия алгебры логики
Основные понятия алгебры логики Аттестационная работа. Проект по созданию мобильных экскурсионных групп
Аттестационная работа. Проект по созданию мобильных экскурсионных групп Животные и растения в устном народном творчестве
Животные и растения в устном народном творчестве Презентация по ОБЖ Пожарная безопасность в России
Презентация по ОБЖ Пожарная безопасность в России  Muslim brotherhood
Muslim brotherhood Векторные пространства
Векторные пространства Презентация "Основы рыночной экономики" - скачать презентации по Экономике
Презентация "Основы рыночной экономики" - скачать презентации по Экономике Языковые средства организации научного знания в логическом позитивизме
Языковые средства организации научного знания в логическом позитивизме Физический и духовный терроризм
Физический и духовный терроризм Фразеологизмы в литературе
Фразеологизмы в литературе Механика материалов. Теории прочности и разрушения. (Лекция 23)
Механика материалов. Теории прочности и разрушения. (Лекция 23)