Содержание
- 2. Инструментальные методы определения напряжений По разгрузке образцов, извлекаемых при бурении (overcoring methods); На основе компенсации напряжений
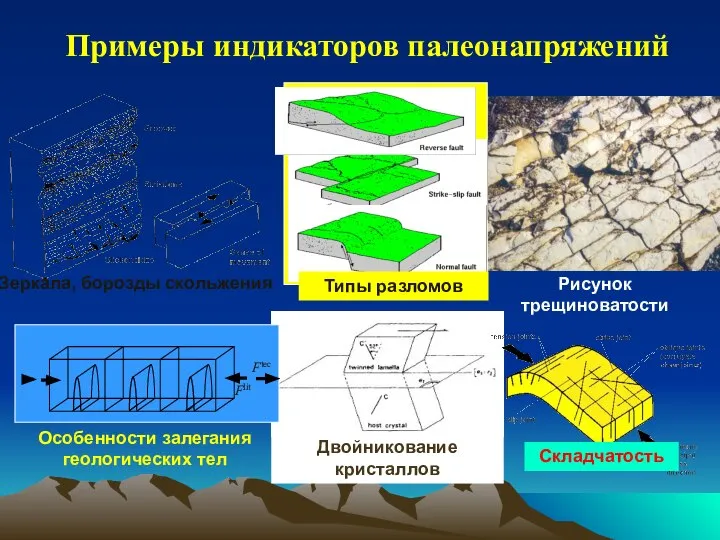
- 3. Примеры индикаторов палеонапряжений Зеркала, борозды скольжения
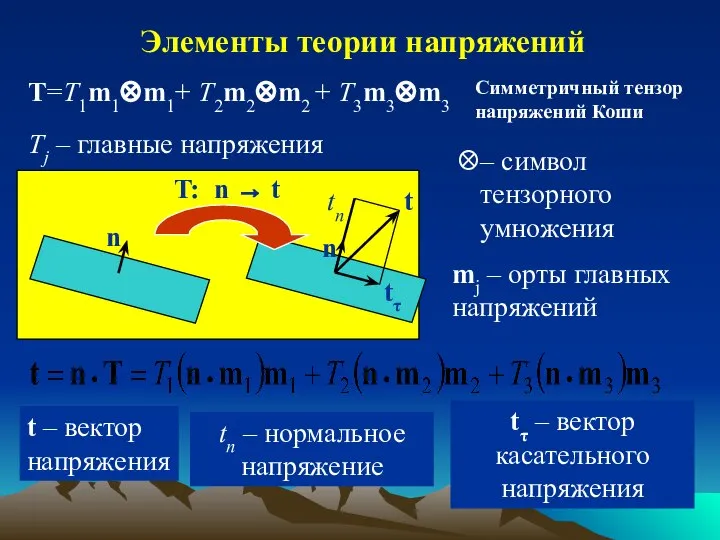
- 4. Tj – главные напряжения mj – орты главных напряжений – символ тензорного умножения T=T1m1⊗m1+ T2m2⊗m2 +
- 5. Элементы теории напряжений Инварианты тензора напряжений
- 6. Элементы теории напряжений ЭКВИВАЛЕНТНЫЕ ТЕНЗОРЫ НАПРЯЖЕНИЙ Примеры представителей Tdev~T Класс эквивалентности однозначно определяется по любому своему
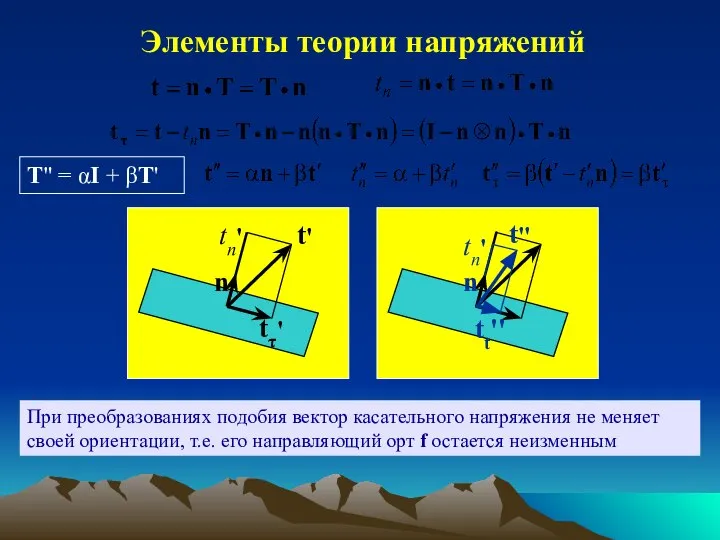
- 7. Элементы теории напряжений t' n tτ' tn' n t'' tn' tt'' T" = αI + βT'
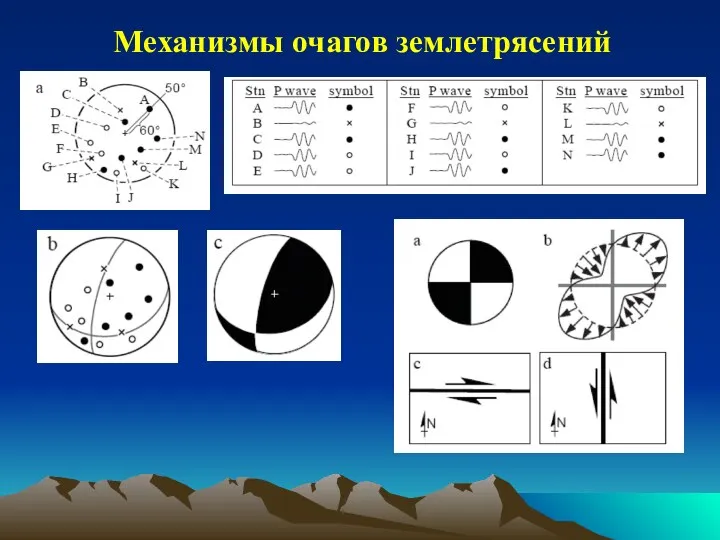
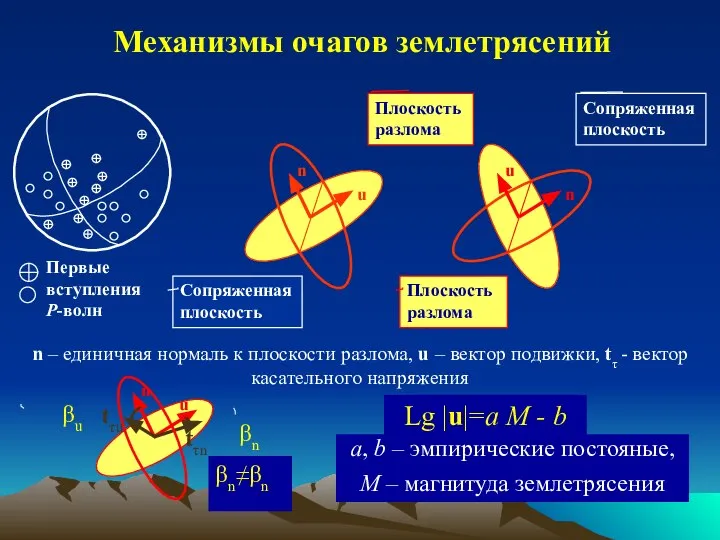
- 8. Механизмы очагов землетрясений
- 9. n – единичная нормаль к плоскости разлома, u – вектор подвижки, tτ - вектор касательного напряжения
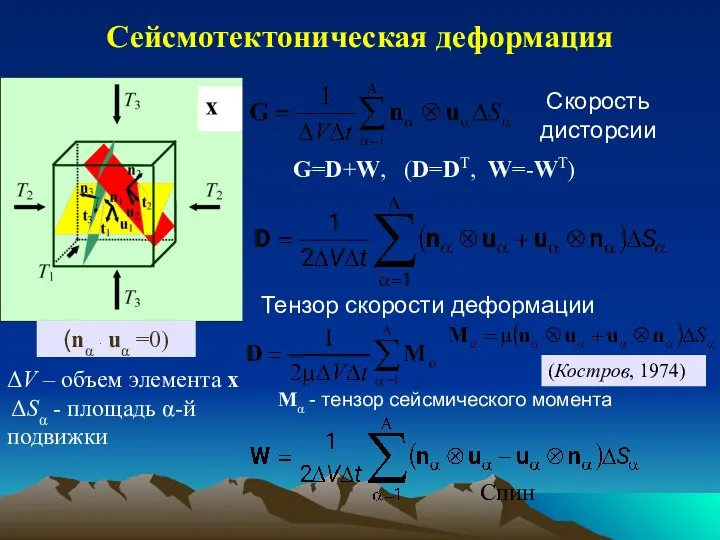
- 10. Сейсмотектоническая деформация G=D+W, (D=DT, W=-WT) ΔV – объем элемента x ΔSα - площадь α-й подвижки (nα
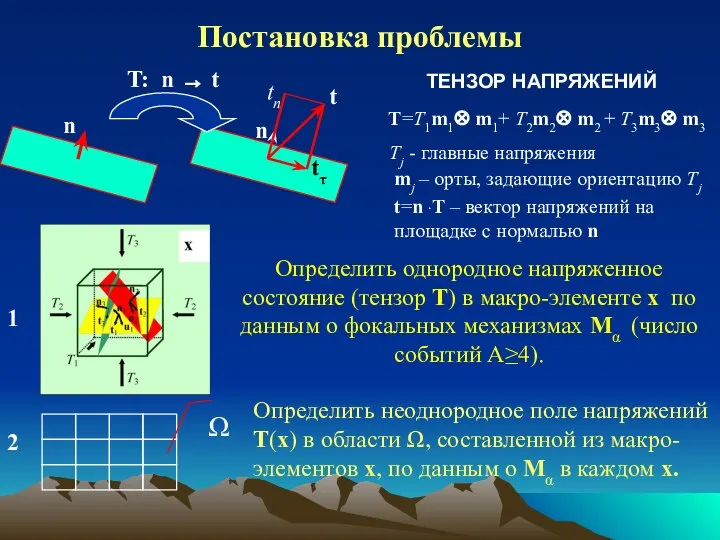
- 11. Постановка проблемы Определить однородное напряженное состояние (тензор T) в макро-элементе х по данным о фокальных механизмах
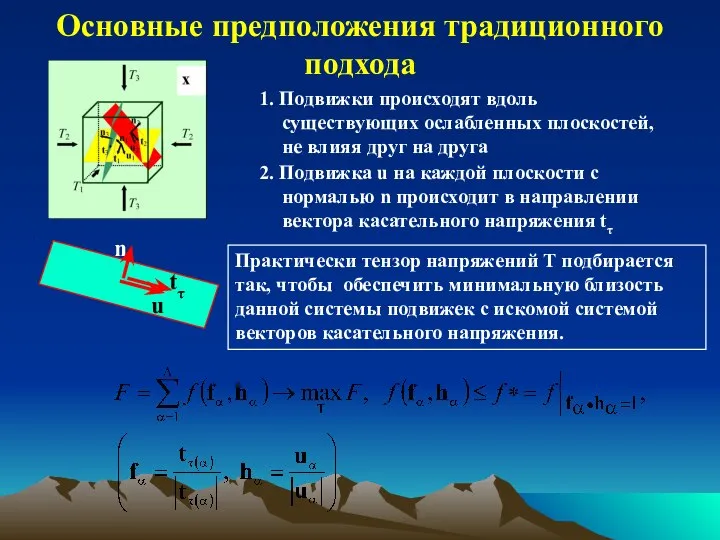
- 12. Основные предположения традиционного подхода Практически тензор напряжений T подбирается так, чтобы обеспечить минимальную близость данной системы
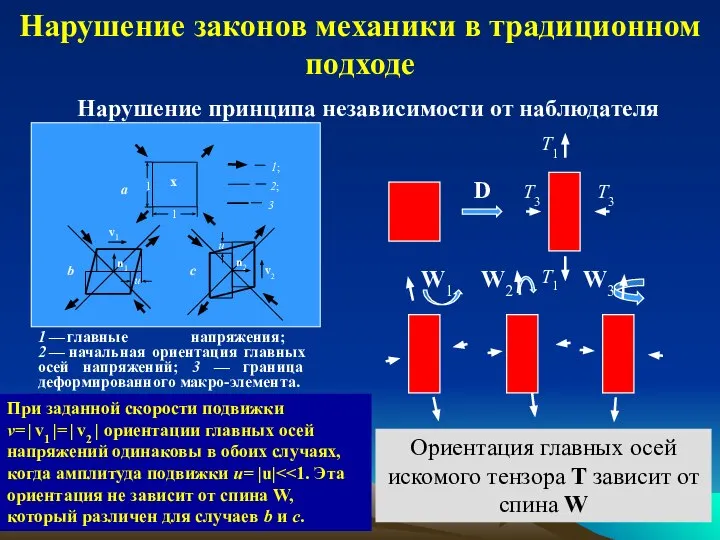
- 13. Нарушение законов механики в традиционном подходе Нарушение принципа независимости от наблюдателя
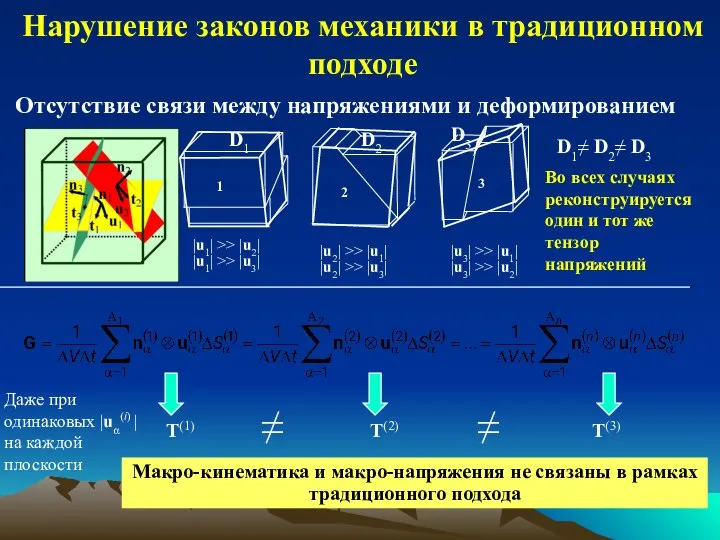
- 14. Макро-кинематика и макро-напряжения не связаны в рамках традиционного подхода Нарушение законов механики в традиционном подходе
- 15. Нарушение законов механики в традиционном подходе В каждом макро-объеме x реконструируются 4 элемента НС: 3 угла
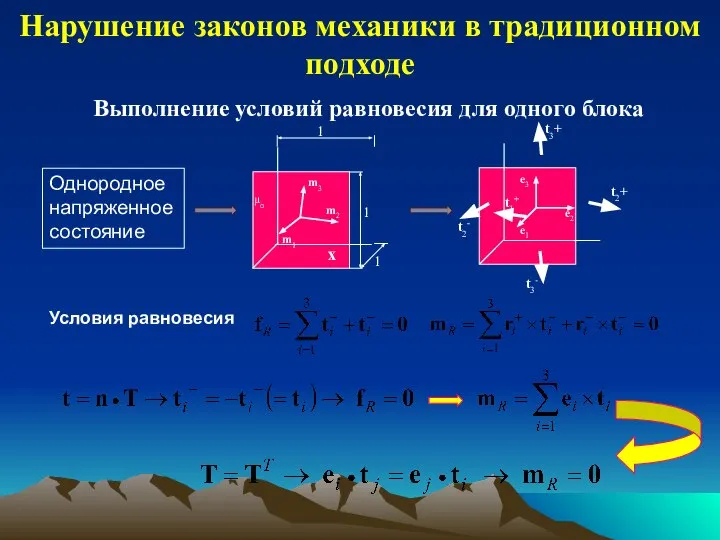
- 16. Нарушение законов механики в традиционном подходе Выполнение условий равновесия для одного блока
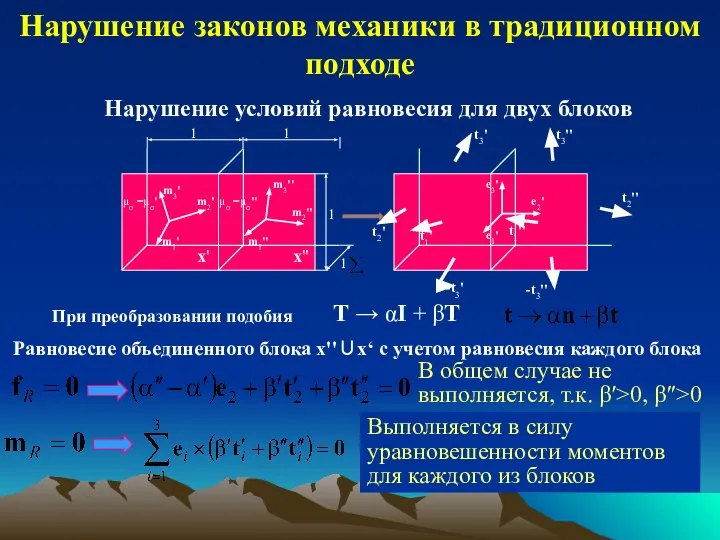
- 17. T → αI + βT При преобразовании подобия Равновесие объединенного блока x''∪x‘ с учетом равновесия каждого
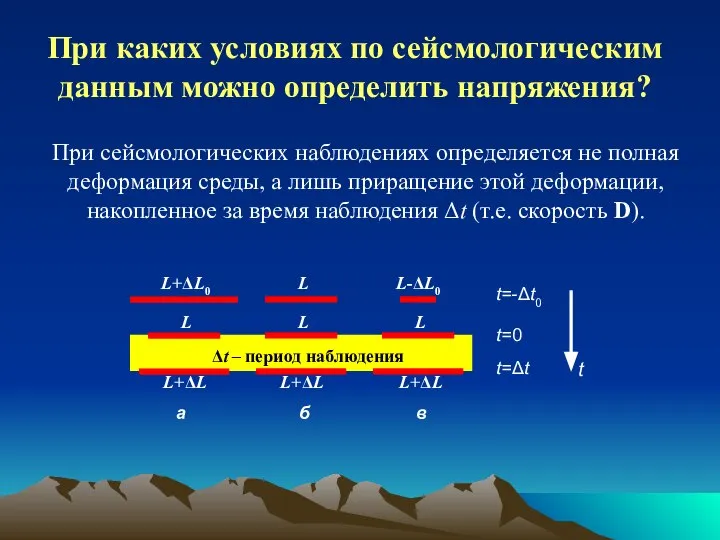
- 18. При каких условиях по сейсмологическим данным можно определить напряжения? При сейсмологических наблюдениях определяется не полная деформация
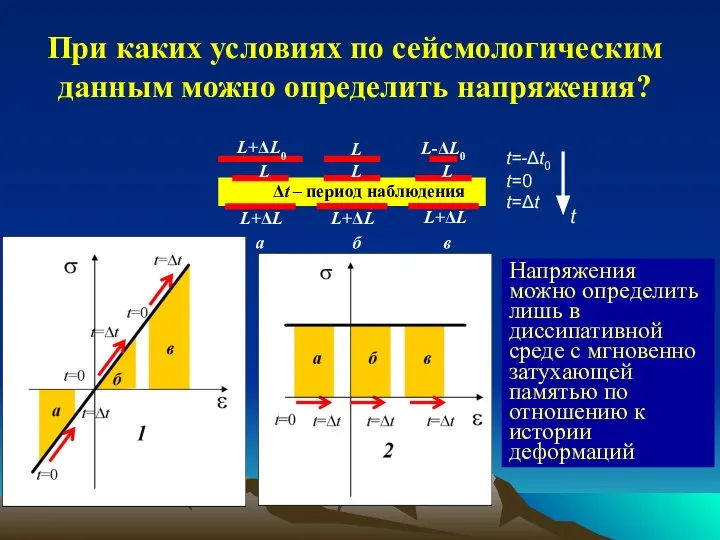
- 19. При каких условиях по сейсмологическим данным можно определить напряжения? Напряжения можно определить лишь в диссипативной среде
- 20. Определяющие соотношения для идеально-пластической среды при условии Принцип экстремума Мизеса
- 21. Определяющие соотношения для идеально-пластической среды
- 22. Определяющие соотношения для идеально-пластической среды Для изотропной функции G(Tdev, …) Определяющие соотношения идеально-пластического тела Изотропная функция
- 23. Трещиноватость осадочных горных пород
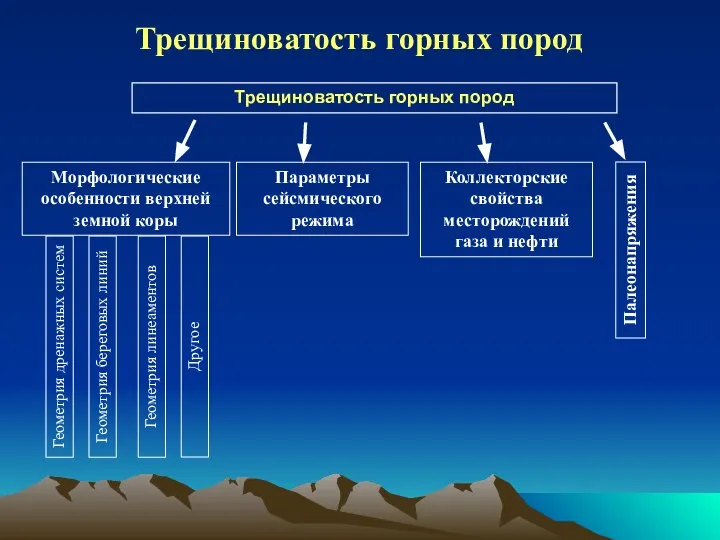
- 24. Трещиноватость горных пород Трещиноватость горных пород Морфологические особенности верхней земной коры Параметры сейсмического режима Палеонапряжения Коллекторские
- 25. Natural exposure Tien-Shan, Kyrgyzstan, 1983 В каждой точке наблюдения (ТН) горным компасом замеряются азимуты (Az) и
- 26. Обработка и интерпретация замеров трещиноватости
- 27. Выделение систем трещин Производится на основе кластерного анализа Первичные системы закладываются на стадии диагенеза осадков .
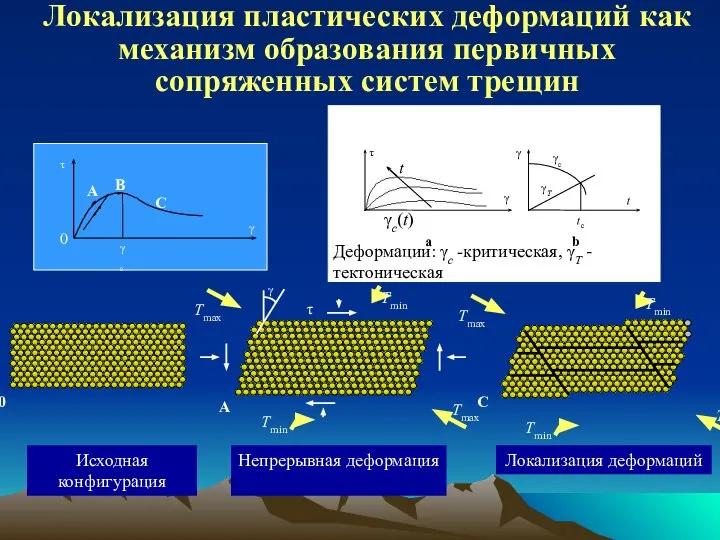
- 28. Локализация пластических деформаций как механизм образования первичных сопряженных систем трещин Исходная конфигурация Непрерывная деформация Локализация деформаций
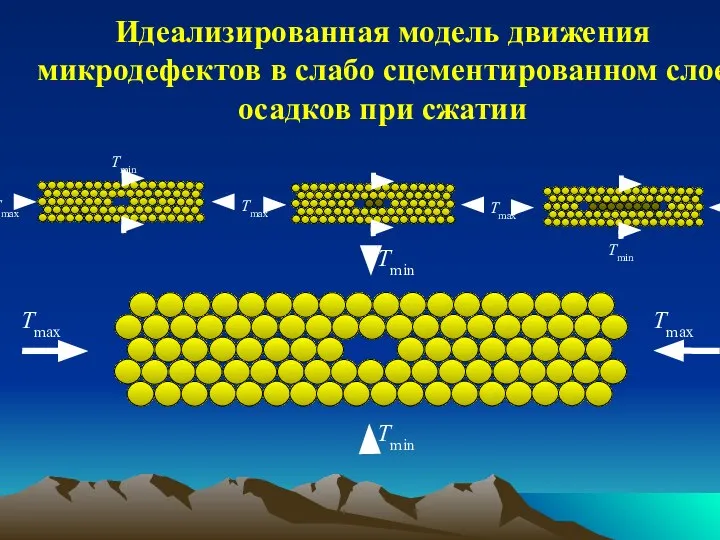
- 29. Идеализированная модель движения микродефектов в слабо сцементированном слое осадков при сжатии Tmax Tmin Tmax Tmin
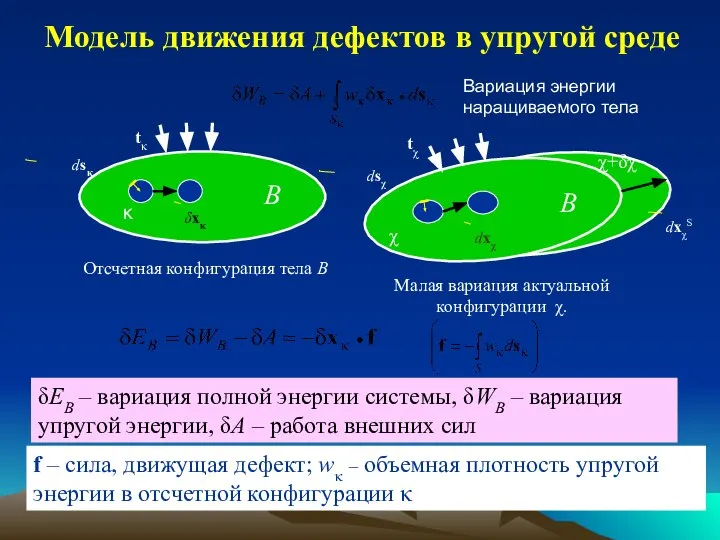
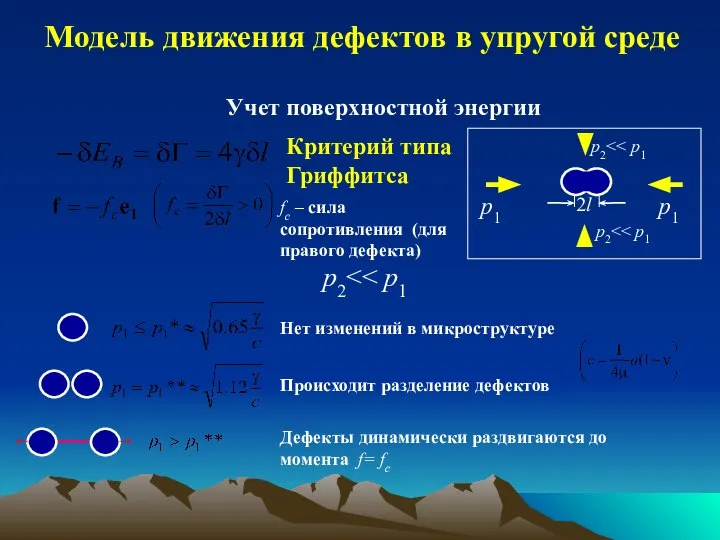
- 30. Модель движения дефектов в упругой среде B δEB – вариация полной энергии системы, δWB – вариация
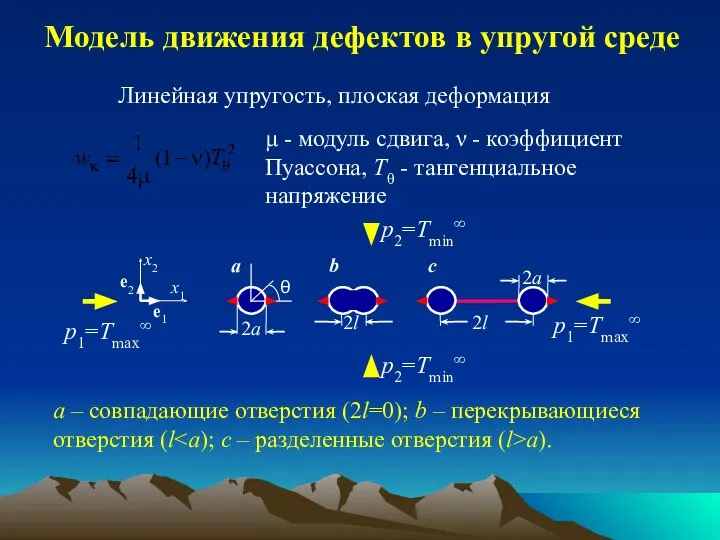
- 31. Линейная упругость, плоская деформация μ - модуль сдвига, ν - коэффициент Пуассона, Tθ - тангенциальное напряжение
- 32. Для определения f используются известные решения. Для l=0 существует аналитическое решение, для ε=a/2l Модель движения дефектов
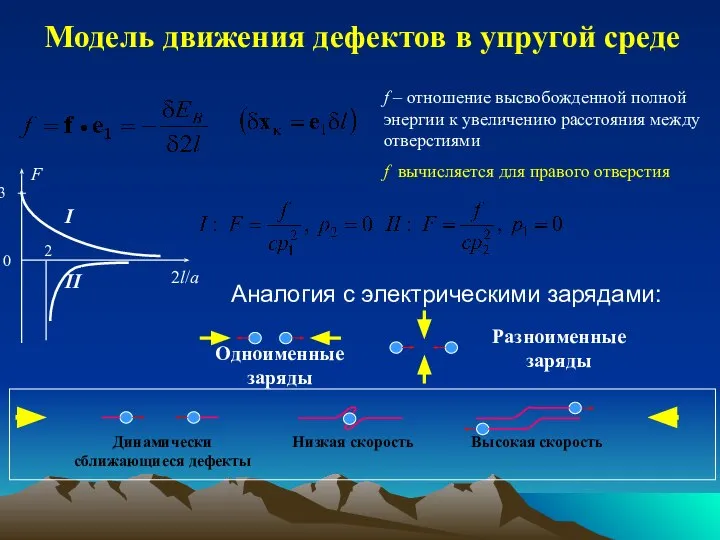
- 33. f – отношение высвобожденной полной энергии к увеличению расстояния между отверстиями f вычисляется для правого отверстия
- 34. Модель движения дефектов в упругой среде
- 35. Обнажение верхнемеловых осадочных пород горных пород (Черноморское побережье Большого Кавказа между Новороссийском и Туапсе) Осадочные слои
- 37. Скачать презентацию













 Алгоритм управления и кибернетика
Алгоритм управления и кибернетика Берлитион
Берлитион  Презентация "Что такое экономика" - скачать презентации по Экономике
Презентация "Что такое экономика" - скачать презентации по Экономике Культура японского народа
Культура японского народа Как проверить, попадает ли ваш земельный участок в приаэродромные территории аэродромов
Как проверить, попадает ли ваш земельный участок в приаэродромные территории аэродромов TABU-элементы: все разрешено, что распространяется само Антон Попов, КИБ 2008
TABU-элементы: все разрешено, что распространяется само Антон Попов, КИБ 2008 Биполярные транзисторы
Биполярные транзисторы Электрические датчики механических величин
Электрические датчики механических величин Політична партія “Україна – вперед”
Політична партія “Україна – вперед” Формулирование собственного высказывания по проблеме профессиональной направленности Урок-тренинг устной и письменной речи
Формулирование собственного высказывания по проблеме профессиональной направленности Урок-тренинг устной и письменной речи Выпуклый анализ. Пространство подмножеств. Лекция 1
Выпуклый анализ. Пространство подмножеств. Лекция 1 «В игре детей есть часто смысл глубокий» Не зная прошлого, нельзя понять настоящего, нельзя ме
«В игре детей есть часто смысл глубокий» Не зная прошлого, нельзя понять настоящего, нельзя ме Начни свое дело с компанией Живая вода
Начни свое дело с компанией Живая вода Hockey-Russia
Hockey-Russia Джеффри Лайкер «Дао Toyota: 14 принципов менеджмента ведущей компании мира»
Джеффри Лайкер «Дао Toyota: 14 принципов менеджмента ведущей компании мира» Талшықты лазер
Талшықты лазер Характер
Характер Сказки гуляют по свету - презентация для начальной школы_
Сказки гуляют по свету - презентация для начальной школы_ Русские народные пословицы и поговорки
Русские народные пословицы и поговорки Ремонт парка пресс-форм. Литьё пластиковых изделий
Ремонт парка пресс-форм. Литьё пластиковых изделий Основы языка C#
Основы языка C# Исполнение наказаний, не связанных с изоляцией осужденных от общества (НСИО). Тема № 6
Исполнение наказаний, не связанных с изоляцией осужденных от общества (НСИО). Тема № 6 Родительское собрание "Стили семейного воспитания"
Родительское собрание "Стили семейного воспитания" Тоталитаризм. Отрицательные черты
Тоталитаризм. Отрицательные черты Творческий проект 8
Творческий проект 8 Русская народная кукла: обычаи и традиции
Русская народная кукла: обычаи и традиции День инвестора Центральной и Восточной Европы (IDCEE) Интернет-технологии и инновации 25-26 октября, 2011 Киев, Украина
День инвестора Центральной и Восточной Европы (IDCEE) Интернет-технологии и инновации 25-26 октября, 2011 Киев, Украина Экспериментальное решение проблемы течи гидроблока МТА
Экспериментальное решение проблемы течи гидроблока МТА