Содержание
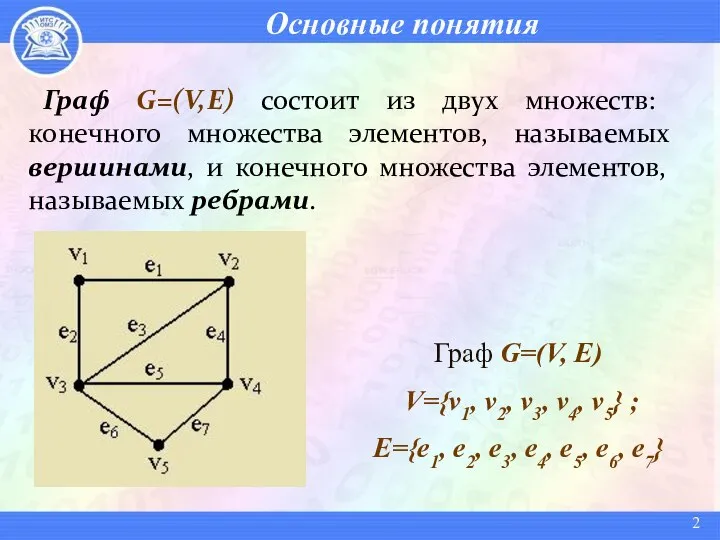
- 2. Основные понятия Граф G=(V,E) состоит из двух множеств: конечного множества элементов, называемых вершинами, и конечного множества
- 3. Основные понятия Вершины vi и vj, определяющие ребро ek, называются концевыми вершинами ребра ek. Ребра с
- 4. Основные понятия Изолированная вершина не инцидентна ни одному ребру (v3). Две вершины смежны, если они являются
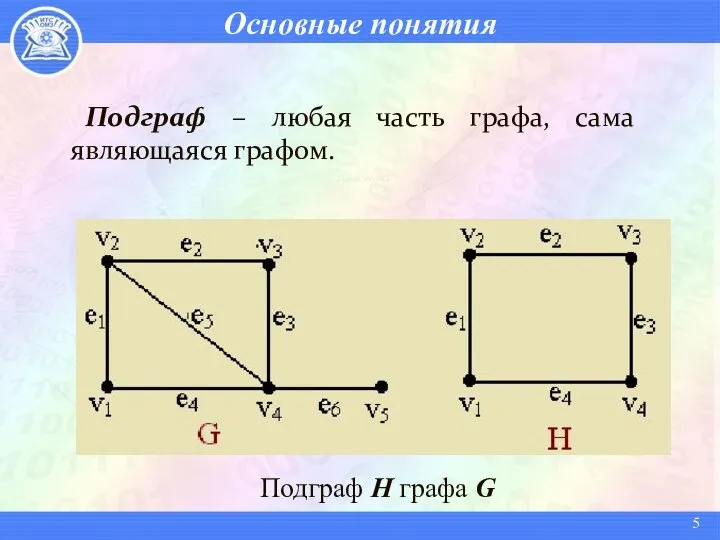
- 5. Основные понятия Подграф – любая часть графа, сама являющаяся графом. Подграф H графа G
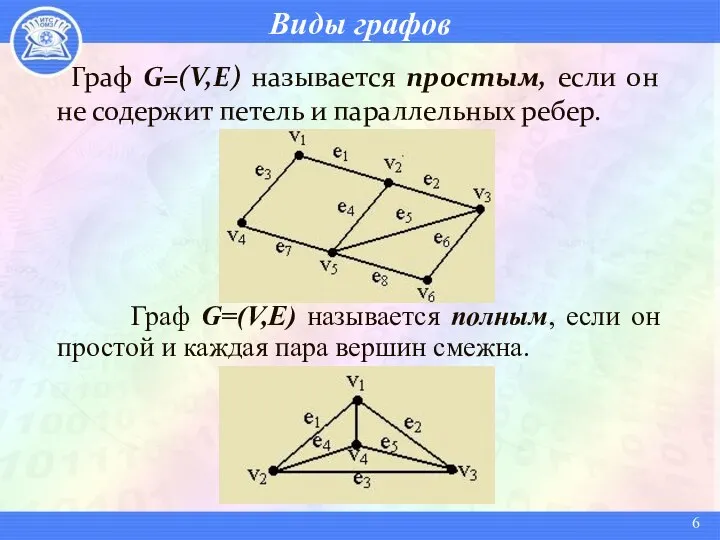
- 6. Виды графов Граф G=(V,E) называется простым, если он не содержит петель и параллельных ребер. Граф G=(V,E)
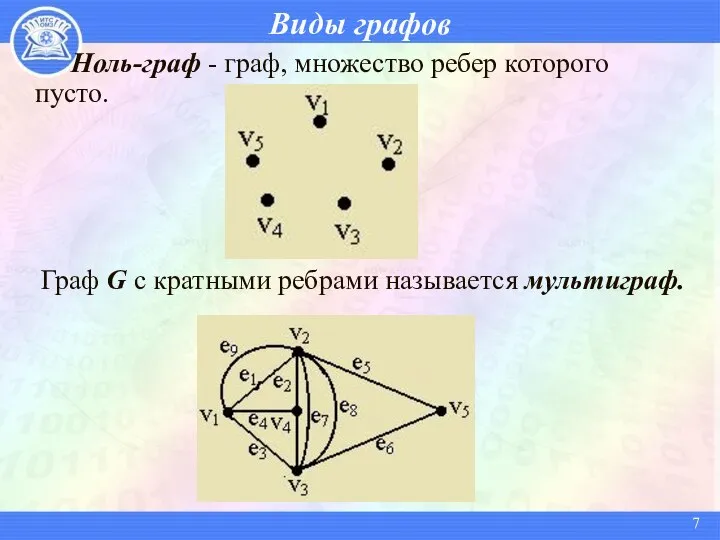
- 7. Виды графов Ноль-граф - граф, множество ребер которого пусто. Граф G с кратными ребрами называется мультиграф.
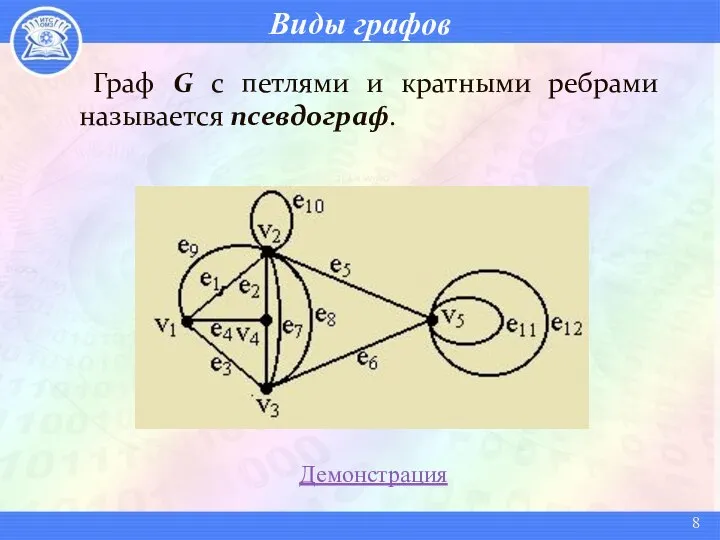
- 8. Виды графов Граф G с петлями и кратными ребрами называется псевдограф. Демонстрация
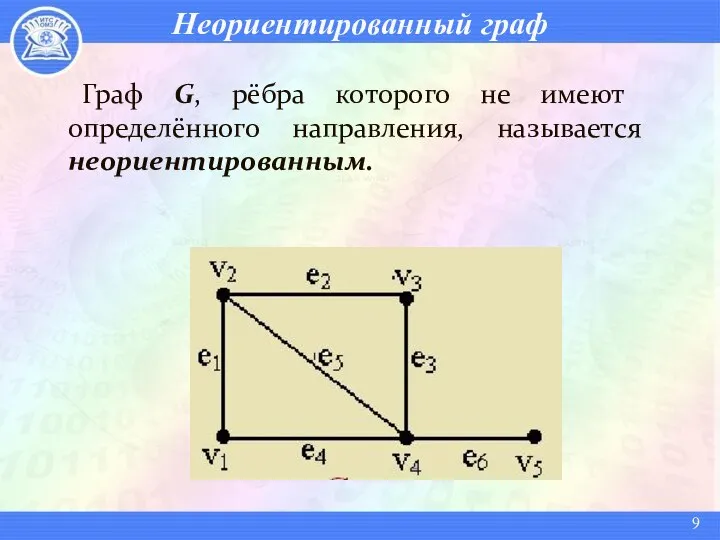
- 9. Неориентированный граф Граф G, рёбра которого не имеют определённого направления, называется неориентированным.
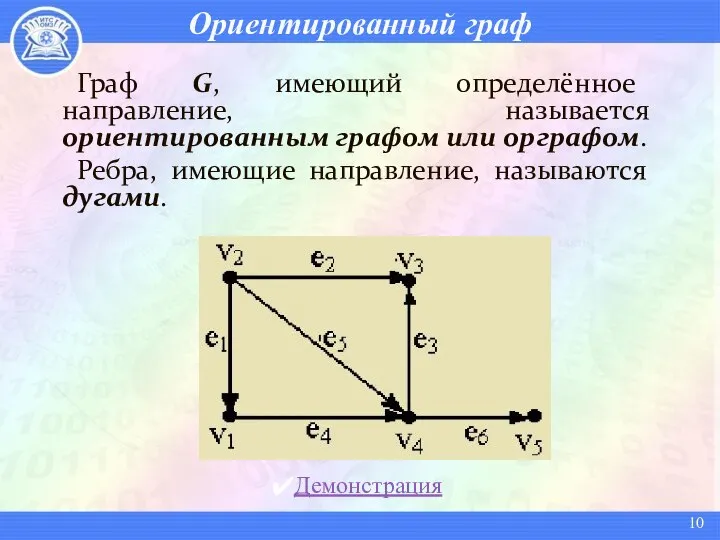
- 10. Ориентированный граф Граф G, имеющий определённое направление, называется ориентированным графом или орграфом. Ребра, имеющие направление, называются
- 11. Способы задания графов 1) Явное задание графа как алгебраической системы. Чтобы задать граф, достаточно для каждого
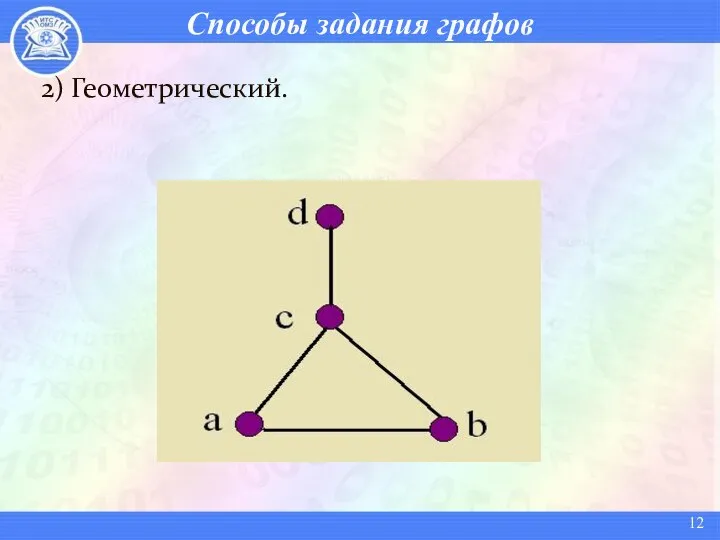
- 12. Способы задания графов 2) Геометрический.
- 13. Способы задания графов 3) Матрица смежности. Элементы Aij матрицы смежности A равны количеству ребер между рассматриваемыми
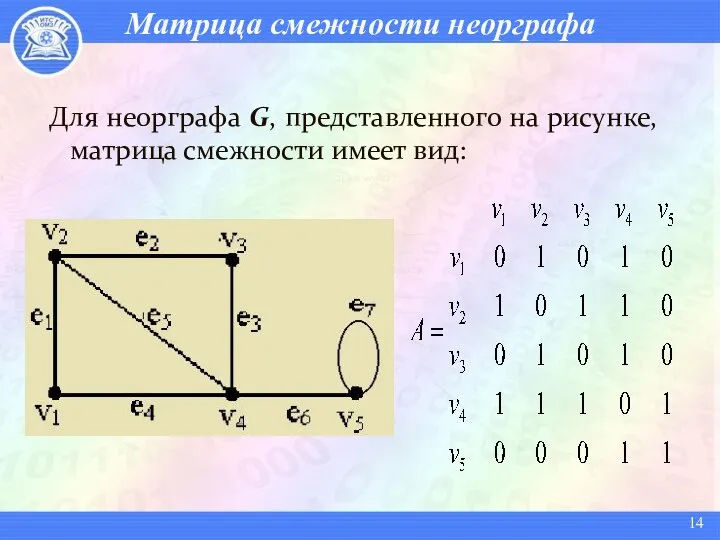
- 14. Матрица смежности неорграфа Для неорграфа G, представленного на рисунке, матрица смежности имеет вид:
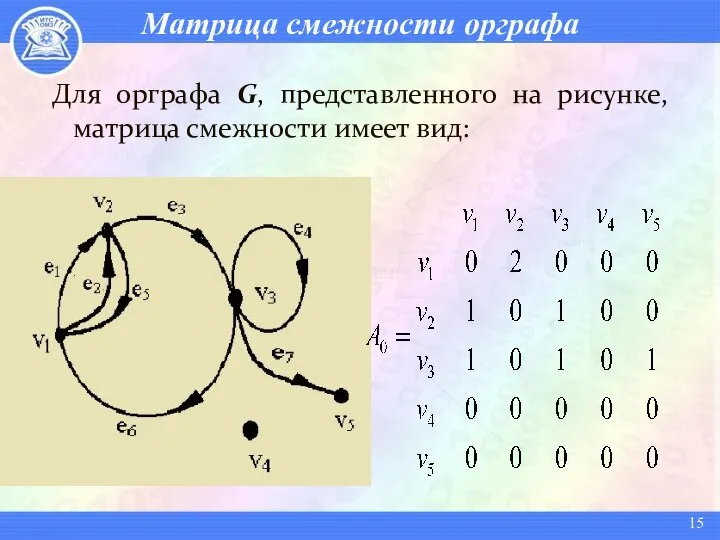
- 15. Матрица смежности орграфа Для орграфа G, представленного на рисунке, матрица смежности имеет вид:
- 16. Способы задания графов 4) Матрица инцидентности. Матрица инцидентности В –это таблица, строки которой соответствуют вершинам графа,
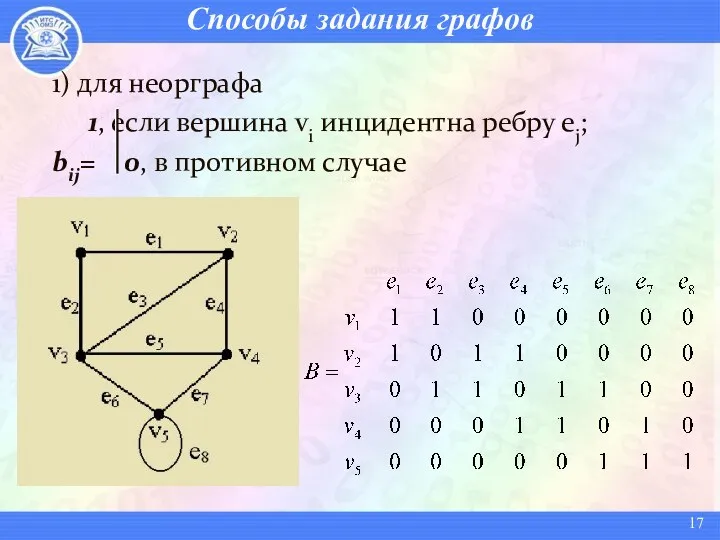
- 17. Способы задания графов 1) для неорграфа 1, если вершина vi инцидентна ребру ej; bij= 0, в
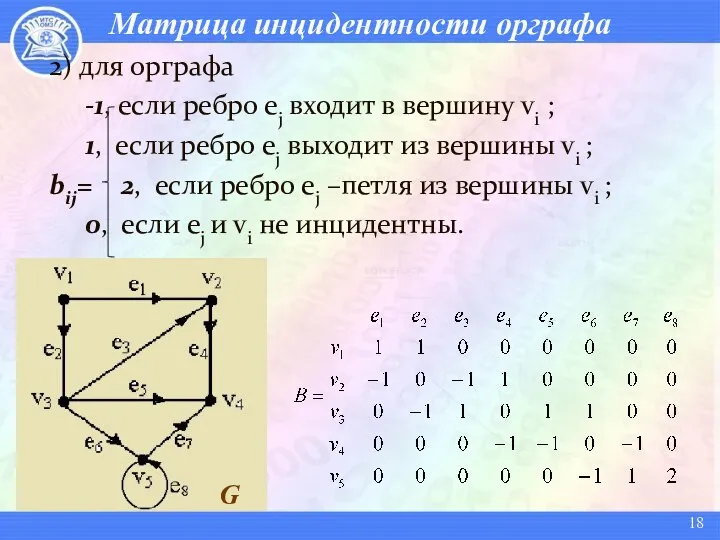
- 18. Матрица инцидентности орграфа 2) для орграфа -1, если ребро ej входит в вершину vi ; 1,
- 19. Маршрут Маршрут в графе G=(V,E) — конечная чередующееся последовательность вершин и ребер v0, e1, v1, e2,…,vk-1,
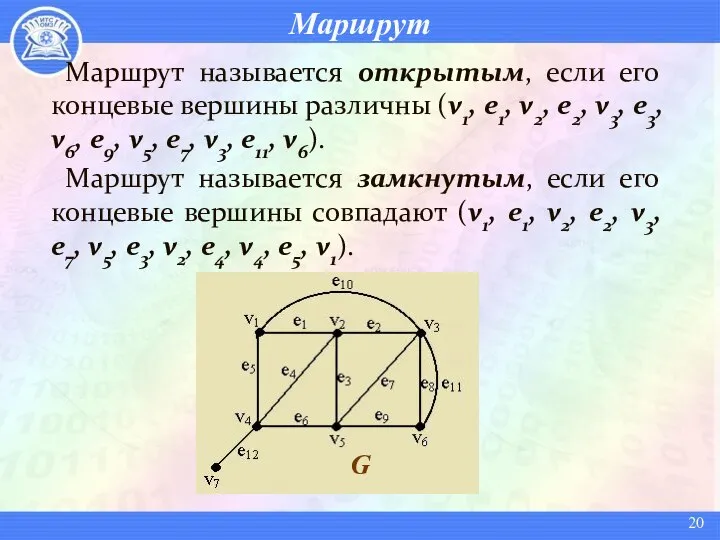
- 20. Маршрут Маршрут называется открытым, если его концевые вершины различны (v1, e1, v2, e2, v3, e3, v6,
- 21. Цепь Маршрут называется цепью, если все его ребра различны. Цепь называется простой, если ее концевые вершины
- 22. Путь, цикл Открытая цепь называется путем, если все ее вершины различны (v1, e1, v2, e2, v3).
- 23. Cвойства путей и циклов 1. Степень каждой неконцевой вершины пути равна 2, концевые вершины имеют степень,
- 24. Связность графов, компонента связности Две вершины vi и vj называются связанными в графе G, если в
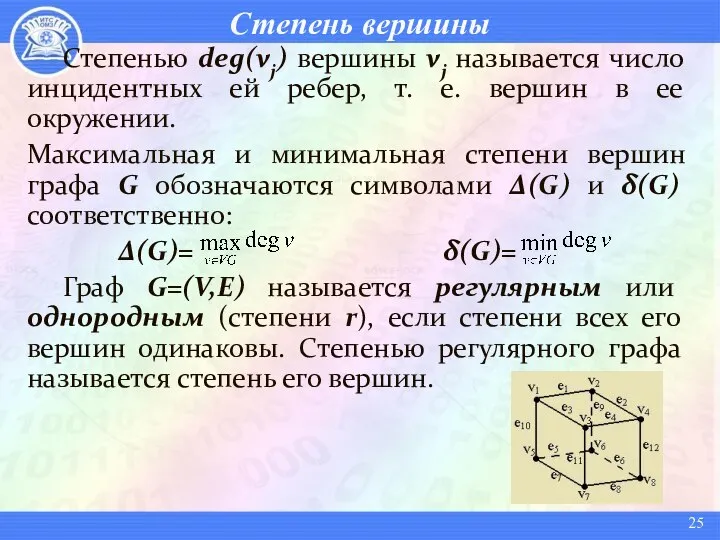
- 25. Степень вершины Степенью deg(vj) вершины vj называется число инцидентных ей ребер, т. е. вершин в ее
- 26. Сумма степеней вершин графа Утверждение («лемма о рукопожатиях») Сумма всех вершин графа – четное число, равное
- 27. Изоморфизм графов Два графа G1 и G2 изоморфны, если существует такое взаимно-однозначное отображение между множествами их
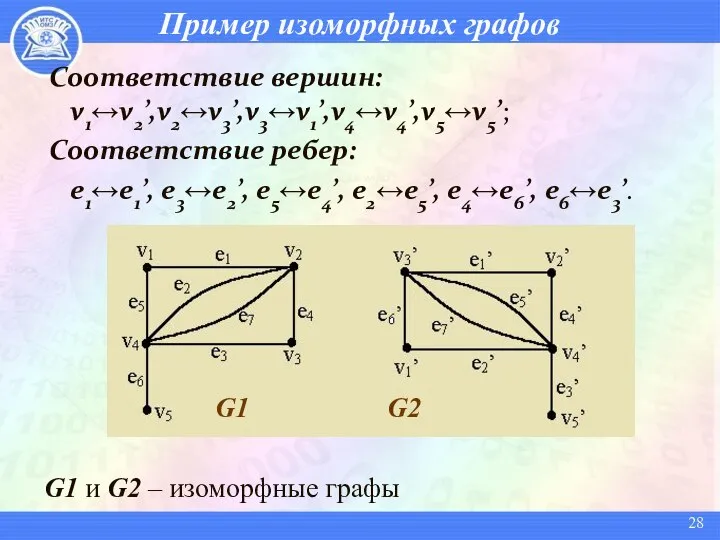
- 28. Пример изоморфных графов Соответствие вершин: v1↔v2’,v2↔v3’,v3↔v1’,v4↔v4’,v5↔v5’; Соответствие ребер: e1↔e1’, e3↔e2’, e5↔e4’, e2↔e5’, e4↔e6’, e6↔e3’. G1 и
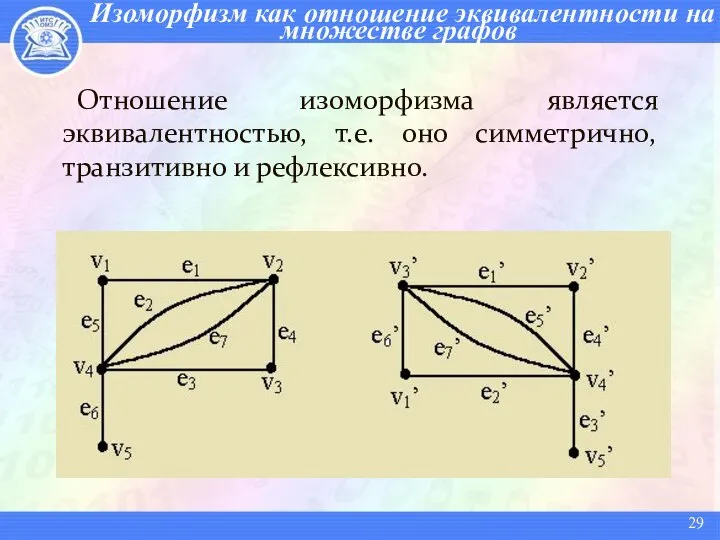
- 29. Изоморфизм как отношение эквивалентности на множестве графов Отношение изоморфизма является эквивалентностью, т.е. оно симметрично, транзитивно и
- 31. Скачать презентацию












 Економічна теорія як наука
Економічна теорія як наука Презентация "Культура СССР начала ХХ века" - скачать презентации по МХК
Презентация "Культура СССР начала ХХ века" - скачать презентации по МХК Мочевыделительная система
Мочевыделительная система Программирование игр на Python
Программирование игр на Python Управление взаимоотношениями с клиентами
Управление взаимоотношениями с клиентами День Благодарения
День Благодарения Артриты и артрозы ВНЧС Выполнила: студентка 5 курса Группы 090716
Артриты и артрозы ВНЧС Выполнила: студентка 5 курса Группы 090716 Сердечная недостаточность
Сердечная недостаточность  ЭКЗИСТЕНЦИАЛЬНО-ГУМАНИСТИЧЕСКИЙ ПОДХОД В ПСИХОЛОГИИ И ПСИХОТЕРАПИИ
ЭКЗИСТЕНЦИАЛЬНО-ГУМАНИСТИЧЕСКИЙ ПОДХОД В ПСИХОЛОГИИ И ПСИХОТЕРАПИИ Жанерке слайд
Жанерке слайд Kinetika2
Kinetika2 Золотые травы Хохломы. «Чудо-ложка»
Золотые травы Хохломы. «Чудо-ложка» Оказание услуг в сфере декорирования джемперов
Оказание услуг в сфере декорирования джемперов Презентация по профессиональной стратификации
Презентация по профессиональной стратификации La arquitectura del Renacimiento (de Lan)
La arquitectura del Renacimiento (de Lan) Школа для развития своего таланта. Проект
Школа для развития своего таланта. Проект Даши Намдаков
Даши Намдаков Das schmeckt gut
Das schmeckt gut Адвокаттың кәсіби әдебі
Адвокаттың кәсіби әдебі О ходе модернизации системы подготовки спортивного резерва в Санкт-Петербурге
О ходе модернизации системы подготовки спортивного резерва в Санкт-Петербурге Поняття та види виборчих систем
Поняття та види виборчих систем УСТРОЙСТВО И ПРИНЦИП РАБОТЫ ЭВМ
УСТРОЙСТВО И ПРИНЦИП РАБОТЫ ЭВМ Лисичка-сестричка и волк
Лисичка-сестричка и волк  Обслуживание и ремонт двигателей постоянного тока
Обслуживание и ремонт двигателей постоянного тока Терминал. Планирование продаж
Терминал. Планирование продаж Современные технологии программирования. λ-выражения в Java 8. Функция как параметр
Современные технологии программирования. λ-выражения в Java 8. Функция как параметр МЕЖПРЕДМЕТНАЯ ИНТЕГРАЦИЯ В ШКОЛЬНОМ КУРСЕ ДИСЦИПЛИН ЕСТЕСТВЕННОГО ЦИКЛА НА ПРИМЕРЕ ПРЕПОДАВАНИЯ БИОЛОГИИ В ШКОЛЕ Аитова Фарид
МЕЖПРЕДМЕТНАЯ ИНТЕГРАЦИЯ В ШКОЛЬНОМ КУРСЕ ДИСЦИПЛИН ЕСТЕСТВЕННОГО ЦИКЛА НА ПРИМЕРЕ ПРЕПОДАВАНИЯ БИОЛОГИИ В ШКОЛЕ Аитова Фарид Филимоновская игрушка (средняя группа)
Филимоновская игрушка (средняя группа)